В данной статье рассматриваются различные закономерности в таблице умножения, их историческое происхождение, применение в школьной математике и в повседневной жизни. Особое внимание уделено связи алгебры и геометрии, а также роли этого знания в развитии логического мышления и памяти. В статье присутствуют примеры, таблицы, задачи с расширенным анализом применения, полезным для школьников.

Таблица умножения является основой арифметики и изучается в начальных классах средней школы. Её знание необходимо для успешного освоения алгебры, геометрии, физики, химии и других дисциплин. Однако она содержит не только сухие числовые факты, но и множество закономерностей, которые помогают лучше понять структуру числового мира. Изучение этих закономерностей полезно не только для развития внимания, памяти, а также формирования логического мышления.

История таблицы умножения уходит в глубь веков. Однозначно сказать, кто придумал таблицу умножения сложно, но различные артефакты были найдены в разных частях Земли. Ещё в Древнем Египте уже более 3000 лет назад использовался метод удвоения для выполнения операций умножения. В Древней Греции и Риме были основой обучения математике, её связывали с трудами Пифагора и поэтому её часто называли “таблица Пифагора”. В Китае 2000 лет назад существовала своя форма таблицы умножения, которая использовалась в школах и передавалась в виде стихов для облегчения запоминания. Археологами были найдены деревянные дощечки с таблицами умножения, относящиеся к I веку до н. э. В Индии таблица умножения применялась для астрономии и алгебры, впервые была чётко систематизирована система десятичного счисления. В Европе её развитие связано с трудами Пифагора и средневековых математиков. В России она появилась в учебниках в XVII веке.

При внимательном рассмотрении таблицы умножения можно заметить ряд закономерностей, здесь представлены некоторые из них:

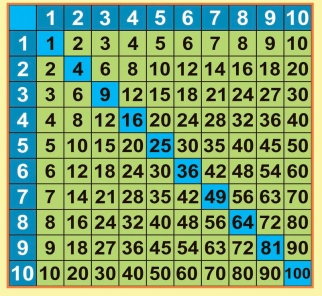
1. Симметрия: произведение a×b=b×a. Это отражает коммутативность умножения и проявляется в зеркальности таблицы относительно главной диагонали.
2. Диагональ: произведения чисел на диагоналях образуют закономерные последовательности, квадраты чисел (1, 4, 9, 16 и т. д.)
3. Чётности и нечётность: произведение двух чётных чисел всегда чётное, а произведение нечётных всегда — нечётное. (2×8=16, 3×7=21)
4. При умножении на 2: окончания повторяются через каждые 5 чисел (2, 4, 6, 8, 0)
5. При умножении на 4: окончания следуют циклом (4, 8, 2, 6, 0)
6. Таблица на 5: произведения заканчиваются на 0 или на 5. (5×2=10, 5×3=15)
7. При умножении на 6: окончания повторяются циклом (6, 2, 8, 4, 0)
8. При умножении на 8: окончания повторяются циклом (8, 6, 4, 2, 0)
9. Таблица на 9: сумма цифр результата всегда ровна 9. (9×2=18, 1+8=9)
10. Таблица на 10: к числу приписывается 0. (7×10=70)
11. Таблица на 11: для чисел до 9 произведение равно повторению цифры (2×11=22)
12. Умножение на 2: это всегда удвоение числа, что легко объясняется геометрически.
13. Последовательность умножения на 4: это удвоение результата при умножении на 2.
14. Суммы строк: сумма чисел в каждой строке образует геометрическую прогрессию.
15. Геометрическая интерпретация: умножение можно трактовать как нахождение площади прямоугольника.
16. Алгебраические свойства: умножение коммутативно и ассоциативно, что отражается в таблице.

С точки зрения алгебры, таблица умножения иллюстрирует такие законы: коммутативность (a×b=b×a), ассоциативность ((a×b) ×с= a×(b×c)) и дистрибутивность или распределительный закон (a×(b+c) =a×b+a×c).

С точки зрения геометрии, умножение можно рассматривать как нахождение площади прямоугольника со сторонами a и b, длина умножить на ширину. Поэтому таблица фактически отражает закономерности построения площадей.

Применение в других областях таблицы умножения связано с физикой — работа с формулами, при решении задач часто приходится выполнять вычисления ч цифрами. В химии — для пропорций и расчёта количества веществ. В информатике — для алгоритмов и работы с массивами данных. В повседневной жизни умение быстро умножать помогает при покупках, кулинарии, планировании и бюджета.

Заучивание таблицы умножения — это не только математическая необходимость, но и важный этап развития памяти, внимания, логического мышления у школьников. Знание таблица умножения позволит быстро решать примеры в уме, возводить в степени и извлекать корни.

Изучение таблицы умножения тренирует память, внимание и воображение. Регулярное повторение числовых комбинаций способствует развитию долговременной памяти. Существуют различные рифмовки и песенки, которые помогают младшим школьникам запомнить быстрее таблицу. В Китае популярны стихотворные формы обучения таблицы, В Японии дети учат её как песню, В Европе и в России используется таблица умножения на бумаге. Сравнение этих методов показывает, что культурные особенности влияют на процесс обучения, но результат — знание таблицы умножения — остаётся универсальным.

Таблица умножения — это не просто школьный материал, а фундамент математики. Она отражает как простейшие арифметические операции, так и глубокие закономерности числового мира. Её изучение помогает понять алгебру и геометрию, формирует логическое мышление и оказывает влияние на развитие памяти и внимания, делает мышление более гибким и развитым. Таким образом, закономерности в таблице умножения играют огромное значение для науки, образования и повседневной жизни.

Литература:

1. Петерсон Л. Г. Математика. 2 класс: учебник для общеобразовательных учреждений. — М.: Ювента, 2013. — Часть 2. — С.81.
2. Баранов С. Таблица умножения за 3 дня. — Ridero, 2021. — С.34.
3. Депман И. Я. История арифметики. — М.: Просвещение, 1985. — С.185.
4. Юшкевич А. П. История математики с древнейших времён до начала XIX столетия. — М.: Наука, 1970. — С.16.