Магические квадраты

Магические квадраты — это квадратные таблицы натуральных чисел, в которых сумма чисел по всем строкам, столбцам и диагоналям одинакова. Порядок квадрата (3, 4, 5, …) определяет количество строк и столбцов. Существуют различные виды магических квадратов, включая четные и нечетные порядки, и для их построения используются специальные формулы. Магические квадраты представляют собой интересный объект изучения в математике.

Исторические корни магических квадратов

Исторические корни магических квадратов уходят глубоко в прошлое человечества, переплетаясь с мифологическими сюжетами, культурой и наукой древних цивилизаций.

1) Китайская культура: ло-шу.

Самые ранние упоминания о магических квадратах происходят из древнего Китая примерно 2800–2200 гг. до нашей эры. Согласно легендам, легендарный правитель Хуан-ди увидел загадочный узор на спине черепахи, плывшей по реке Ло. Узор представлял собой магический квадрат 3×3, называемый «ло-шу».

2) Индийская математика и астрономия.

Индия стала следующей территорией распространения магических квадратов. Упоминания о них содержатся в трактате IX века Шридхарачарьи, известного индийского математика. Некоторые древние индуистские храмы украшены резными магическими квадратами, демонстрируя глубокое уважение к магии чисел и геометрии.

3) Арабская наука и философия.

В период Средневековья магические квадраты распространились в мусульманском мире благодаря работам арабских математиков и философов. Одним из первых исследователей была школа Аль-Хорезми, основоположника алгебры. Арабские учёные активно использовали магические квадраты в астрологии, медицине и тайнописи. Среди выдающихся работ выделяется книга Абу-ль-Вафа ибн Мухаммад аль-Бузджани (X век), в которой подробно описаны принципы составления магических квадратов.

4) Европейская эпоха Возрождения.

В эпоху Возрождения магические квадраты привлекли внимание европейской интеллигенции. Итальянский учёный Лука Пачоли посвятил значительное внимание исследованию магических квадратов в своей книге «Об удивительных силах количеств» (около 1500 г.). Позже великий живописец Альбрехт Дюрер создал знаменитый магический квадрат на своей гравюре «Меланхолия I».

Современная наука продолжает исследовать магические квадраты, раскрывая новые возможности их применения в криптографии, статистике, архитектуре и дизайне. Несмотря на многовековую историю, магические квадраты продолжают вдохновлять новых поколений математиков и любителей искусства своими изящными свойствами и красотой формы.

Классические примеры. Виды магических квадратов

1. Магический квадрат Ло-шу (Китайская традиция):

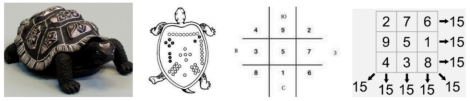
Рис. 1. Магический квадрат Ло-шу

2. Магический квадрат Дюрера («Меланхолия I»):

Рис. 2. Магический квадрат Дюрера

3. Панмагический квадрат Агриппы (4х4, магическая сумма — 34).
4. Классический квадрат 5х5 (магическая сумма — 65).
5. Квадрат Гансена-Росенталя (7х7, магическая сумма — 175).

Стоит различать магические квадраты нечетного и четного порядка.

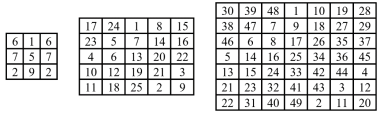
Рис. 3. Магические квадраты нечетного порядка (3х3, 5х5, 7х7)

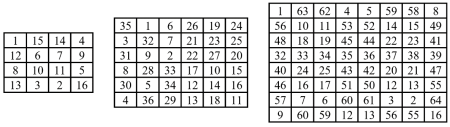
Рис. 4. Магические квадраты четного порядка (4х4, 6х6, 8х8)

Способы создания магических квадратов

1) Для создания магических квадратов нечетного порядка используется метод Сиама:

1. Пишем число 1 в центре верхней строки.
2. Следующее число размещаем в направлении «вправо-вверх»:

– Если выходим за пределы квадрата сверху, переходим на нижнюю строку.

– Если выходим справа, то перемещаемся влево на первую колонку.

– Если там позиция занята, то ставим число внизу текущего элемента.

3. Повторяем шаги до заполнения всего квадрата.

Рассмотрим применение алгоритма к построению квадрата 3х3.

Рис. 5. Составление квадрата 3х3 по алгоритму

Этот метод идеально подходит для заполнения нечетных магических квадратов (5х5, 7х7, 9х9 и т. д.).

2) Для четных магических квадратов обычно применяют метод Латинского квадрата или специальные алгоритмы для конкретных случаев: квадраты порядка 4k (двойной четности) и квадраты порядка 4k+2 (одинарной четности: делится на 2, но не делится на 4).

Рассмотрим алгоритм составления магических квадратов порядка одинарной четности на примере составления квадрата 6х6. Его магическую константу вычислим по формуле, сумме n первых членов арифметической прогрессии: (n*(n ² +1))/2, получим 111.

1. Разделим магический квадрат на четыре квадранта A, B, C и D одинакового размера (3х3). Разместим их как показано на рисунке.
2. В каждый квадрант надо вписать по 9 чисел: в квадранте А напишем числа 1–9; в квадранте В — числа 10–18; в квадранте С — числа 19–27; в квадранте D — числа 28–36.
3. Числа в каждом квадранте запишем так, как мы строили нечетный квадрат. Квадрант А начнем заполнять числами с 1, а квадранты С, B, D — с 10, 19, 28, соответственно. Эти числа разместим в центральной ячейке верхней строки каждого квадранта.
4. Заполняем каждый квадрант числами так, как будто это отдельный магический квадрат. На данном этапе сумма чисел в столбцах, строках и по диагонали еще не будет равна магической константе. Необходимо поменять местами числа в определенных ячейках верхнего левого и нижнего левого квадрантов.
5. Поменяем местами числа из выделенных областей А и D. Теперь сумма чисел в любой строке, столбце и по диагонали равна магической константе.

Рис. 6. Составление магического квадрата 6х6, порядка одинарной четности

3) Ручное составление большого магического квадрата трудоемко и подвержено ошибкам. Для упрощения процесса можно использовать специализированные алгоритмы и инструменты программирования. В настоящее время с этой задачей хорошо справляется ИИ.

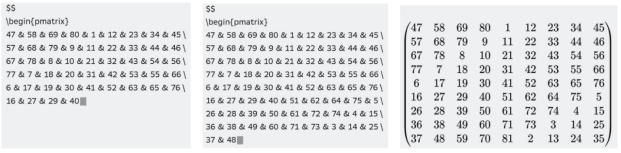
Рис. 7. Составление магического квадрата 9х9 с помощью ИИ

4) Существует и трехмерная версия магического квадрата — магический куб. Классическим магическим кубом порядка n называется куб размерами n × n × n, заполненный различными натуральными числами от 1 до n ³ так, что суммы чисел в любом из 3n ² рядов, параллельных ребрам куба, а также на четырех (пространственных) диагоналях куба равны одному и тому же числу, называемому магической константой куба.

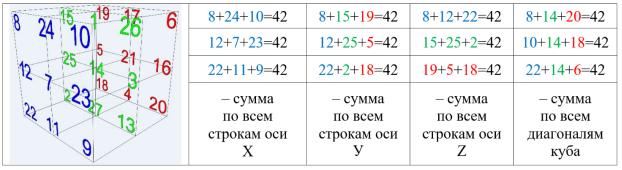
Рис. 8. Магический куб 3х3х3 и его константа

На основе квадрата Дюрера построена геометрическая фигура «куб в кубе» (магические квадраты Кхаджурахо, Дюрера и Золотая Пропорция). Подобное «преобразование» стало возможным при расположении вертикальных столбцов чисел квадрата Дюрера под определенным углом, образуя, таким образом, куб в кубе. При этом все числа диагоналей куба обладают свойством «золотой симметрии», а плоскости, имеющие 4 угла как внутреннего, так и внешнего квадратов, образуют в сумме число 34.

Заключение

1. Создание собственных магических квадратов — прекрасный способ развить интуицию и почувствовать себя творцом уникальной числовой композиции.
2. Правильно выбранный метод позволяет эффективно построить магический квадрат нужного порядка. Каждый метод ориентирован на специфические размеры и имеет свои особенности реализации.
3. Создание магического куба на основе магических квадратав — это верх совершенства и истинное мастерство.

Литература:

1. Черепаха, которая выползла из реки Ло: a_nasta_siya — ЖЖ — черепаха из реки Ло.
2. Как решить магический квадрат — wikiHow — создание магических квадратов.
3. Магический куб — Википедия — изображение магического куба.