Введение

Эта задача известна с 1612 года, когда французский математик Баше опубликовал эту задачу в своём сборнике Problem es Plaisants. Сюжет задачи основан на истории, описанной Иосифом Флавием в своём историческом труде «Иудейская война».

Согласно этой истории, Иосиф Флавий со своим отрядом из сорока человек после падения Йодфата скрылся в пещере, но был обнаружен римлянами. Все в отряде, кроме Иосифа, предпочли совершить самоубийство, но не сдаваться в плен. Иосиф пытался отговорить своих товарищей от самоубийства и сдаться. Однако они обвиняли его в трусости и хотели убить своего командира. Тогда Иосиф Флавий предложил солдатам встать в круг и убивать каждого третьего. Баше спрашивает, где нужно встать Иосифу и его товарищу, чтобы остаться последними, на кого выпадет жребий.

В более общей формулировке данная задача звучит так: по кругу стоят n воинов с номерами 1, 2, …, n и начиная отсчет с первого номера убивают каждого k-го воина. Необходимо определить начальное положение выжившего воина.

В данной работе введены следующие обозначения:

J(n;k) — номер выжившего воина, когда их было первоначально n и убивали каждого k-го воина.

J(n;k;m) — номер воина убитого на m-ом ходе, когда их было первоначально n и убивали каждого k-го воина.

1. Классическая задача Иосифа Флавия.

1. Рекурректные соотношения.

Согласно [1], если известно решение задачи для некоторого числа воинов, то его можно использовать для решения задачи с на единицу большим числом воинов.

Для общего случая имеем при :

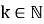
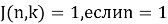
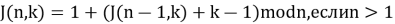
Возможно построение рекуррентных соотношений, которые сходятся намного быстрее чем линейные. Вот пример решения задачи для k = 2 с логарифмическим числом шагов рекурсии:

(1)

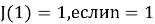
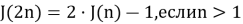
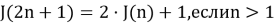
При программировании приведенные выше рекуррентные соотношения дают вычислительную сложность и соответственно. Получение решения в виде формулы приводит к алгоритмам, в которых вычислительная сложность минимальна — , т. е. вообще не зависит от n и k.

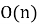
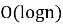
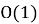
2. Нахождение формулы для решения задачи Иосифа Флавия.

Найдем решение задачи Иосифа Флавия в виде формулы при k = 2 используя рекуррентные соотношения (1).

Если n = 2 ^m последовательно имеем:

=

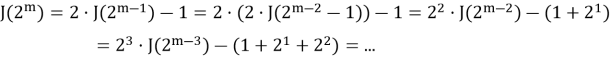
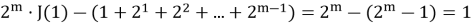
Мы использовали, что сумма геометрической прогрессии

.

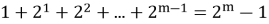
Окончательно,

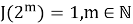
Найдем , где l = 2 ^p и .

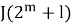
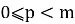
Также последовательно получаем:

=

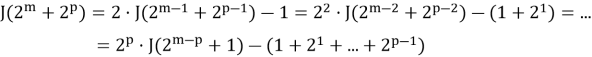
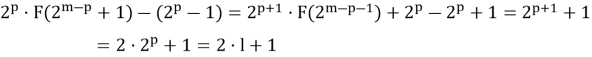
Предположим, что в общем случае формула имеет вид:

, где и . (2)

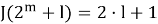
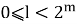
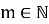
Обратим внимание, что если , то тогда остаток удовлетворяет .

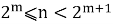
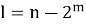
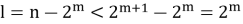
Данную формулу (2) можно доказать непосредственно подставляя разложение l по степеням двойки: , где и .

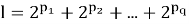
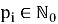
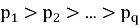
Мы же докажем данную формулу с помощью метода математической индукции по m.

База индукции: При m=0 мы должны иметь l=0, таким образом ,что верно.

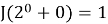
Предположение индукции: .

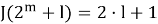
Шаг индукции будет состоять из двух частей в зависимости от того четно или нечетно l.

Если m>0 и ,тогда l — четно и

. Предположение верно.

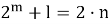
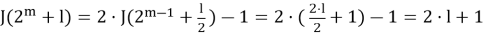
Если m>0 и ,тогда l — нечетно и

. Предположение верно.

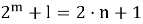
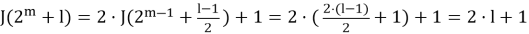
Шаг индукции завершен.

Выпишем полученные результаты в виде таблицы:

n	1	2	3	4	5	6	7	8	9	10	11	12
J(n;2)	1	1	3	1	3	5	7	1	3	5	7	9
J(n;2) mod4	1	1	3	1	3	1	3	1	3	1	3	1

n	13	14	15	16	17	18	19	20	21	22	23	24
J(n;2)	11	13	15	1	3	5	7	9	11	13	15	17
J(n;2) mod4	3	1	3	1	3	1	3	1	3	1	3	1

n	25	26	27	28	29	30	31	32	33	34	35	36
J(n;2)	19	21	23	25	27	29	31	1	3	5	7	9
J(n;2) mod4	3	1	3	1	3	1	3	1	3	1	3	1

Запишем полученную формулу в немного другом виде:

, (3)

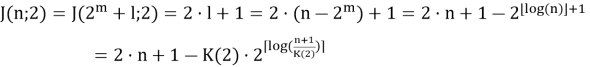
где K(2)=1 и логарифм имеет основание 2.

В [2] приведена формула для решения классической задачи Иосифа Флавия при k = 3:

, (4)

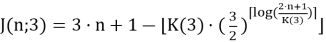
где K(3)=1,62227050288476731595695098289932411...

В данной формуле (4) логарифм имеет основание .

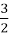
Тогда решение первоначальной задачи Иосифа Флавия:

.

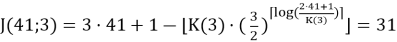
Возникает предположение, что формула для решения задачи Иосифа Флавия при k = q имеет вид:

, где

(5)

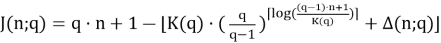
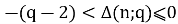
В данной формуле (5) логарифм имеет основание .

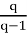
Насколько мне известно, на данный момент, предположение о верности формулы (5) остается открытой проблемой. Таким образом закон изменения величин Δ (n;q) и K(q) неизвестен.

Возможно, .

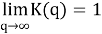
3. Алгоритмы для нахождения решения задачи Иосифа Флавия

Так же существуют алгоритмы (в т. ч. на основании рекурректных соотношений) позволяющие вычислить значение . Например, в [3] приведен алгоритм, с моей точки зрения, наиболее простой для нахождения решения классической задачи Иосифа Флавия.

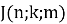
а) Нам необходимо найти номер последнего выжившего.

Принимаем и .

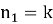
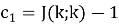
Приведем краткую таблицу для определения при :

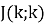
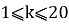
k	1	2	3	4	5	6	7	8	9	10
J (k;k)	1	1	2	2	2	4	5	4	8	8
k	11	12	13	14	15	16	17	18	19	20
J (k;k)	7	11	8	13	4	11	12	8	12	2

Последовательно вычисляем:

(6)

(7)

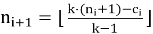
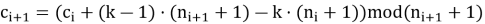
Если , то тогда принимаем .

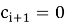
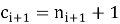
Когда выполнится условие решение классической задачи Иосифа Флавия будет в виде:

(8)

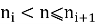
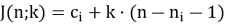
б) Нам необходимо определить номер выбывшего на m-ом шаге ( ).

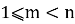
Принимаем и , если или

, если .

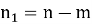
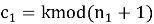
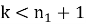
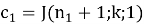
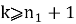
Используя формулы (6) и (7) последовательно вычисляем и .

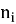
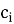
Когда выполнится условие решение классической задачи Иосифа Флавия будет в виде:

(9)

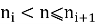
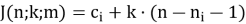
Примеры.

а) Необходимо найти J(41;3)(Первоначальная задача Иосифа Флавия).

Имеем n = 41, k = 3, J(3;3) = 2. Тогда n1 = 3 и c1 = 1.

Получаем:

i	1	2	3	4	5	6	7
n i	3	5	8	13	20	30	46
c i	1	1	1	2	2	1	2

Тогда J(41;3) = 1+3*(41–30–1) = 31.

б) Необходимо найти J(117;6).

Имеем n = 117, k = 6, J(6;6) = 4. Тогда n ₁ = 5 и c ₁ = 3.

Получаем:

i	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17
n i	6	7	9	11	13	16	20	24	29	35	42	51	61	73	88	106	127
c i	3	1	3	3	1	2	5	4	4	4	3	5	3	1	2	3	1

Тогда J(117;6) = 3+6*(117–106–1) = 63.

в) Необходимо найти J(117;6;46).

Имеем n = 117, k = 6, m = 46. Тогда n ₁ = 71 и c ₁ = 6.

Получаем:

i	1	2	3	4
n i	71	85	102	123
c i	6	4	3	5

Тогда J(117;6;46) = 3+6*(117–102–1) = 87.

г) Необходимо найти J(41;3;40) (Первоначальная задача Иосифа Флавия).

Имеем n = 41, k = 3, m = 40. Тогда n ₁ = 1 и c ₁ = J(2;3;1) = 1.

i	1	2	3	4	5	6	7	8	9
n i	1	2	4	6	10	15	23	35	53
c i	1	1	2	1	2	1	1	1	1

Тогда J(41;3;40) = 1+3*(41–35–1) = 16.

д) Необходимо найти J(n;k;m). Где n = 11111111111111111111111, k = 7,

m = 11111111111111111109110. Здесь число n имеет 23 знака (!).

Мы имеем n ₁ = 2001 и c ₁ = 7. После долгих(!) арифметических вычислений найдем n ₂₈₀ < n < n ₂₈₁ , где n ₂₈₀ = 9538759184899654873314 и c ₂₈₀ = 5.

Тогда J(n;7;m) = 5+7*(n — n _280– 1) = 11006463483480193664577.

Желающие могут сравнить данное решение с альтернативным решением этой же задачи опубликованном в [4].

2. Обобщенная задача Иосифа Флавия

1. Задача Иосифа Флавия с множественным выбыванием.

Немного изменим исходную задачу: По кругу стоят n воинов с номерами 1, 2, …, n и начиная отсчет с первого номера убивают

k-го, (k+1)-го, …, (k+(s-1))-го воина и т. д. Необходимо определить начальные положения выживших воинов.

Частный случай данной задачи рассмотрен в работе [5]. К сожалению в данной работе в окончательной формуле допущена опечатка.

Наиболее полное решение задачи Иосифа Флавия с множественным выбыванием при k=2 приведено в работе [6].

Пусть количество выживших воинов — P ( ), .

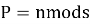
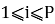
Представим первоначальное число воинов n в виде: , (10)

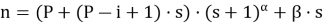
где α и β — целые неотрицательные числа, притом α — максимально возможная степень.

Тогда номер i-го выжившего после I-ой итерации:

(11)

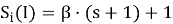
Пример.

Найти J (207,2,4,i).

Имеем n = 207, k = 2, s = 4, , .

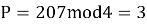
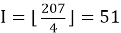
Для i = 1 имеем: и , α = 1 и β = 33.

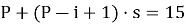
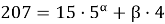
Тогда номер первого выжившего: S ₁ (51) = 33*5+1 = 166.

Для i = 2 имеем: и , α = 1 и β = 38.

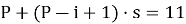
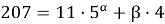
Тогда номер второго выжившего: S ₂ (51) = 38*5+1 = 191.

Для i = 3 имеем: и , α = 2 и β = 8.

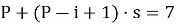
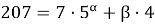
Тогда номер третьего выжившего: S ₃ (51) = 8*5+1 = 41.

Насколько мне известно, в общем виде (при произвольном k) приведенная выше задача на данный момент не решена.

2. Задача Иосифа Флавия с множественными пересадками.

2.1. Играя с друзьями в определении номера выжившего воина в классической задаче Иосифа Флавия при k = 2 у меня возник вариант следующей задачи (здесь мы убивать воинов не будем):

За круглым столом сидят n воинов с номерами 1, 2, …, n и начиная отсчет с первого номера каждого k-го воина пересаживают на свободное место за другим столом, и так продолжается до тех пор пока все воины не разместятся за новым столом. Затем также они пересаживаются за третий стол и так t раз. Необходимо определить начальное положение воина последним севшим за (t+1)-ый стол.

Например, для n = 9 пересадки выглядят следующим образом:

1 стол	2 стол	3 стол	4 стол	5 стол	6 стол	7 стол	8 стол	9 стол	10 стол
1	2	4	8	7	9	3	6	5	1
2	4	8	7	9	3	6	5	1	2
3	6	5	1	2	4	8	7	9	3
4	8	7	9	3	6	5	1	2	4
5	1	2	4	8	7	9	3	6	5
6	5	1	2	4	8	7	9	3	6
7	9	3	6	5	1	2	4	8	7
8	7	9	3	6	5	1	2	4	8
9	3	6	5	1	2	4	8	7	9

Как можно заметить существует замкнутая «петля» номеров воинов посидевших на последнем (в нашем случае девятом) стуле каждого стола: . Длина данной

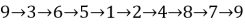
«петли» — 9 номеров. Таким образом можно сказать, что последним за 123-ий стол сядет воин с первоначальным номером 2 (123=9*13+6).

Данная «петля» номеров в нашем примере одинакова для каждого стула, например, для первого стула каждого стола: .

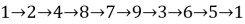
А для n = 10 пересадки выглядят следующим образом:

1 стол	2 стол	3 стол	4 стол	5 стол
1	2	4	8	1
2	4	8	1	2
3	6	3	6	3
4	8	1	2	4
5	10	5	10	5
6	3	6	3	6
7	7	7	7	7
8	1	2	4	8
9	9	9	9	9
10	5	10	5	10

Здесь существует 3 «петли» номеров разной длины: (длина L ₁ =4); (длина L ₂ =2); (длина L ₃ =2).

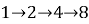
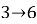
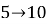
А также 2 «стационарных» стула с номерами 7 и 9. Т. е. воины сидевшие первоначально за первым столом на стульях с номерами 7 и 9 за любым другим столом сидят на стульях с такими же номерами.

Как можно заметить, что в данном примере, всегда на последнем стуле любого стола будут сидеть воины под номерами 5 и 10 — в зависимости от четности номера стола.

Количество пересадок для возвращения к первоначальной рассадке воинов: N _пер = НОК (L ₁ ;L ₂ ;…;L _i ), где i — количество «петель».

2.2. Найдем алгоритм, позволяющую нам рассчитывать получающиеся «петли».

Для этого воспользуемся формулой (3), тогда получаем, что

(12)

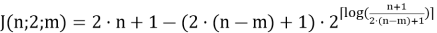
Используя формулу (12) получаем следующий алгоритм нахождения последовательности номеров при многократной пересадке:

1) Находим по формуле (3) номер воина последним севшим за 2-ой стол .

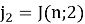
2) Тогда номер воина последним севшим за k-ый стол :

, если или

, если .

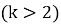
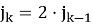
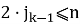
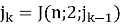
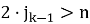
3) Повторяем пункт 2, пока не получим замкнутую «петлю» номеров.

Пример.

Пусть количество воинов за первым столом n = 34.

Тогда «петля» номеров воинов, которые сидят на последнем стуле каждого стола:

, длиной L ₁ =11 номеров.

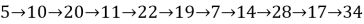
Другие «петли»:

, длиной L ₂ =11 номеров;

, длиной L ₃ =7 номеров;

, длиной L ₄ =4 номера.

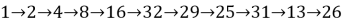
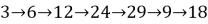
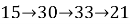
«Стационарный» номер: 23.

Количество пересадок, для возвращение воинов к первоначальной рассадке: N _пер = НОК (L ₁ ;L ₂ ;L ₃ ;L ₄ ) = НОК (11;11;7;4) = 308.

2.4. Найдем формулу позволяющую находить «стационарные» номера при многократной пересадке.

Воспользуемся формулой (12). Получаем

(13)

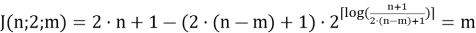
Так как , где .

, где и

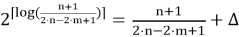
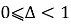
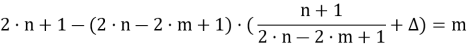
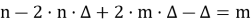
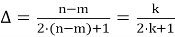
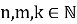
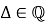
Значит

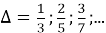
Составляем таблицу:

	Δ = 1/3		Δ = 2/5		Δ = 3/7		Формула
	m	n	m	n	m	n
k=1	3	4	5	7	7	10	n=3p+1, m=2p+1
k 1 =3k	9	10	15	17	21	24	n=7p+3, m=6p+3
k 2 =7k	21	22	35	37	49	52	n=15p+7, m=14p+7
k 3 =15k	45	46	75	77	105	108	n=31p+15, m=30p+15

Как можно заметить n и m описываются формулами:

(14)

(15)

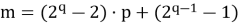
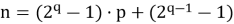
где и .

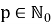
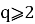
Действительно, подставляя формулы (14) и (15) в формулу (13) получаем верное равенство.

Заполним таблицу для нахождения n и m при разных q и p:

	q=2		q=3		q=4		q=5		q=6
	m	n	m	n	m	n	m	n	m	n
p=0	1	1	3	3	7	7	15	15	31	31
p=1	3	4	9	10	21	22	45	46	93	94
p=2	5	7	15	17	35	37	75	77	155	157
p=3	7	10	21	24	49	52	105	108	217	220
p=4	9	13	27	31	63	67	135	139	279	283
p=5	11	16	33	38	77	82	165	170	341	346
p=6	13	19	39	45	91	97	195	201	403	409
p=7	15	22	45	52	105	112	225	232	465	472
p=8	17	25	51	59	115	127	255	263	527	535
p=9	19	28	57	66	133	142	285	294	589	598
p=10	21	31	63	73	147	157	315	325	651	661

Окончательно, если число воинов n описывается формулой (15), то тогда «стационарные» номера описываются формулой (14).

Если же число воинов n можно получить разным набором q и p, то тогда для данного n будет несколько «стационарных» номеров.

Например, n = 31. Тогда m = 21 (при q=2, p=10), m = 27 (при q=3, p=4) и

m = 31 (при q=6, p=0).

В [7] приведен алгоритм нахождения решения задачи с другим способом рассадки игроков:

Дано n игроков, пронумерованных от 1 до n, расположенных последовательно за круглым столом, и k — положительное целое число ( ). Предположим, что после удаления игроков, как в задаче Иосифа Флавия, последний удалённый игрок помещается на первую позицию за вторым столом. Оставшиеся n − 1 игроков возвращаются на свои исходные позиции на первом столе и снимаются с игры ещё раз, последний из них занимает первую свободную позицию на втором столе. Этот процесс повторяется, пока все игроки не окажутся на втором столе. Затем они снимаются (на этот раз со второго стола), и последний из них объявляется победителем. Задача состоит в том, чтобы заранее предсказать начальную позицию G(n, k) (на первом столе) последнего оставшегося игрока на втором столе.

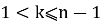
3. Другие варианты задачи Иосифа Флавия.

3.1 «Кошачья» задача Иосифа Флавия

В отличие от классической задачи Иосифа Флавия вводят число жизней L, так что воины не удаляются, пока не будут выбраны в L-й раз.

Решение данной задачи приведено в [8].

3.2. Задача Иосифа Флавия при различных модулях

Следующий тип задач рассмотрен в [9]:

Предположим, что есть 14 человек. Начинают убивать каждого второго человека, но двоих одновременно. Первый процесс исключения начинается с первого человека, а второй — с восьмого. Предполагается, что первый процесс идёт первым на каждом этапе. Следовательно, последовательно будут исключены следующие номера 2, 9, 4, 11, 6, 13, 8, 1, 12, 5, 3, 10, 14, и остаётся 7.

Литература:

1. https://ru.wikipedia.org/wiki/Задача_Иосифа_Флавия
2. M. Odlyzko and H. S. Wilf, Functional iteration and the Josephus problem, Glasgow Mathematical Journal 33 (2) (1991), 235–240.
3. S. Uchiyma, On the generalized Josephus promlem, Tsukuba J. Math, Vol. 27, № 2 (2003), 319–339.
4. L. Halbeisen and N. Hungerbühler, The Josephus Problem, Journal de Thèorie des Nombres de Bordeaux, 9 (1997), 303–318.
5. Н. А. Карамач, З. К. Кот, Е. А. Баркова, О задаче Иосифа Флавия, 54-я научная конференция аспирантов, магистрантов и студентов БГУИР, 2018, 131–134.
6. J. W. Park and R. Teixeira, Serial execution Josephus problem, Korean J. Math, 26 (2018), № 1, pp. 1–7.
7. N. Theriault, Generalizations of the Josephus problem, Utilitas Mathamatica 58, (2000), 161–173.
8. F. Ruskey and A. Williams, The Feline Josephus Problem, Theory of Computing Systems, 50, (2012) 20–34.
9. Yamauchi, Toshiyuki; Inoue, Takahumi; and Tatsumi, Soh (2009), Josephus Problem Under Various Moduli, Rose-Hulman Undergraduate Mathematics Journal: Vol. 10: Iss. 1, Article 10.