Целью исследования является разработка кода, который по первым двум ходам партии сможет определять ее исход со 100-процентной точностью. Для этого автор проанализировал и систематизировал возможные тактические линии в игре «Крестики-нолики». Все разработанные автором алгоритмы созданы на основе моделирования и анализа сюжета партии. Они основываются на создании комбинаций-ловушек, загоняющих противника в тупик, и не оставляющих шансов на победу. Понимание работы описанных алгоритмов позволяет спрогнозировать исход партии по ее первым двум ходам. Результатом работы стало написание программного кода «X/O-444» («Крестики-нолики — 444») на языке программирования Python, который со 100-процентной точностью прогнозирует исход партии при вводе координат первых двух ходов.

Введение

Правила игры в крестики-нолики очень просты, поэтому эта игра весьма популярна в повседневной жизни людей самых разных возрастов и социальных групп. Каждый игрок стремится победить и как можно реже проигрывать, однако периодически это оказывается весьма затруднительно. Не углубившись в теоретическую часть этой игры, невозможно полностью избежать поражений, поскольку «игра в крестики-нолики заставляет нас погрузиться в дебри весьма нетривиальных проблем» [1, C.49].

В данном исследовании проведен анализ вариантов построения беспроигрышных комбинаций и оборонительных тактических линий. Результаты исследования позволили разработать и написать не имеющий аналогов программный код, который со 100-процентной точностью определяет исход партии в «Крестики-нолики» по результатам ее первых двух ходов. Дальнейшее развитие проекта возможно в виде разработки игрока-робота, в алгоритмы которого будут заложены результаты данного исследования. На сегодняшний день есть приложения для игры в «Крестики-нолики» из коллекций «Яндекс-игры», Logic games, Wordpass и др., однако программные коды в этих приложениях работают линейно: они не прогнозируют исход партии, не строят комбинаций-ловушек и, соответственно, не выдают защиту от таких комбинаций-ловушек со стороны игрока, поэтому обыграть программу становится достаточно легкой задачей.

В ходе исследования автор ознакомился с теорией игр и некоторыми работами, в которых выигрышные стратегии интеллектуальных логических игр рассматриваются с точки зрения математики: «Математические головоломки и развлечения» М. Гарднера [1], «Занимательная математика» Я. И. Перельмана [2], «По следам Пифагора» М. Еленьского [3].

В своей работе «Математические игры» д-р Вильгельм Аренс пишет, что «с математической точки зрения наибольший интерес представляют задачи сравнительно несложные. Для сложных игр, среди которых, по своему образовательному значению, первое место занимает шахматная игра, трудно, да едва ли и возможно найти исчерпывающую теорию, охватывающую все частные случаи, теорию, которая для каждой мыслимой позиции дала бы возможность найти абсолютно лучший ход и выиграть начинающему или, еще лучше, при безошибочной игре обоих игроков сыграть вничью» [1. C.7]. Поэтому для своего научно-исследовательского дебюта, автор выбрал несложную в моделировании сюжета и простую для понимания, по сравнению с такими играми как шашки, и, тем более, шахматы, но всеми любимую и популярную игру в «Крестики-нолики».

Основное содержание

Задача данного проекта — разработать программный код, которой сможет определять исход партии при вводе координат первых двух ходов партии. Для этого был проведен анализ топографии поля, тактического преимущества каждой клетки поля, и разработаны алгоритмы беспроигрышной игры при старте с той или иной позиции. Рассмотрим более детально математику на игровом поле «Крестиков-ноликов» и углубимся в алгоритмы создания беспроигрышных комбинаций-ловушек.

Топография поля. Типы клеток. Вопреки расхожему мнению, что в начале партии у первого игрока есть выбор из 9 возможных вариантов хода, существует только три уникальных варианта — это ход в центральную клетку (B2), ход в одну из боковых клеток (B1, B3, A2, C2) и ход в одну из угловых клеток (A1, A3, C1, C3). См.Рис.1. Все остальные варианты начала партии являются их симметричными эквивалентами. В статье подробно рассматриваются преимущества начала партии каждым из трех вариантов и описаны комбинации-ловушки и противодействия им.

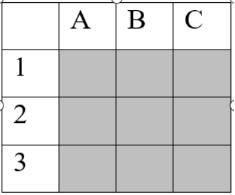
Рис. 1

Ловушки и противодействия. Центральная клетка. С первого взгляда может показаться, что центральная клетка B2 имеет самое важное стратегическое значение для захвата контроля над ходом всей партии. Заняв эту клетку, мы лишаем противника возможности выполнения трех типов комбинаций-ловушек из четырех (о них ниже), а реализация четвертой комбинации-ловушки становится затруднительной. Мы также лишаем противника возможности ходить на клетки B1, А2, С2, B3, а перед нами открывается возможность сыграть комбинацию-ловушку. Игрок, занявший клетку B2 делает следующий ход в клетку A1, C1, A3 либо C3, не соседствующую с клеткой, занятой противником, ставя ему шах. Противник вынужден закрываться, и этим ходом ставит шах первому игроку. Первый игрок защищается, играя, таким образом, комбинацию-ловушку (рис.2).

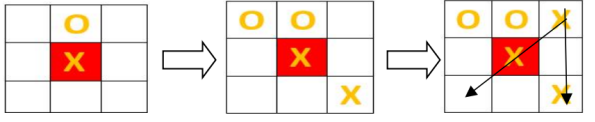
Рис. 2

Боковая клетка. Ход в эту клетку является нестандартным началом партии, т. к. игроки зачастую недооценивают силу этой клетки (A2, B1, B3, C2) и считают ее стратегически невыгодной, поскольку она открывает возможность для построения лишь двух финальных выигрышных линеек. Однако, это не совсем правильно. Эта клетка может удивить возможностью построения 2 тактических линий для создания комбинации-ловушки. Рассмотрим пример с первым ходом партии на клетку B3. Если противник отвечает ходом в клетки С2 или симметричную клетку A2, первый игрок ответит ходом в клетку B2, не оставив противнику иного хода, как оборона в клетке B1. Первый игрок получает возможность сыграть комбинацию ловушку B3-B2-A3 или B3-B2-C3, если второй хода партии был в клетку С2 (рис.3).

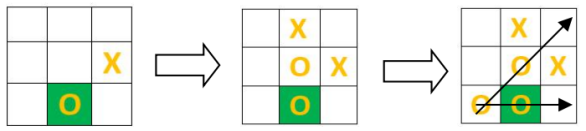
Рис. 3

Рассмотрим второй вариант использования этой комбинации-ловушки, создание которой возможно, если противник ходит в угол, не соседствующий с клеткой первого хода — B3 (А1 и C1). Первый игрок ходит в клетку С3, соседствующую со своим первым ходом. Второй игрок вынужден держать оборону ходом А3, одновременно ставя шах первому игроку, и первый игрок разыгрывает третью из рассматриваемых в статье комбинаций-ловушек B3-B2-C3 (рис.4).

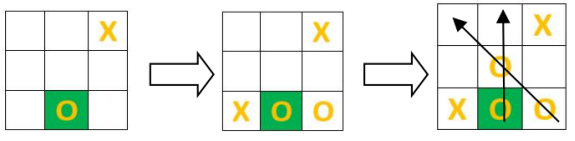
Рис. 4

Таким образом, начало партии с боковой клетки является неожиданным и нестандартным стартом. Из-за фактора неожиданности не уступает тактике начала с клетки B2.

Угловая клетка. Игроки часто считают угловую клетку (A1, C1, A3, C3) не самой стратегически выгодной для начала партии. Но, на самом деле, это самая перспективная клетка, т. к. дает возможность для формирования целых трех комбинаций-ловушек, а из 8 оставшихся возможных ходов второго игрока, 6 неминуемо приведут к поражению.

Разыграть первую из предложенных автором комбинаций возможно, если на ход первого игрока в клетку А3, второй игрок отвечает ходом B3. Первый игрок блокирует единственную возможность второго игрока выстроить финальную линию ходом B2, ставя ему шах. Второй игрок защищается ходом C1. Отвечая ходом A2 первый игрок разыгрывает беспроигрышную комбинацию A3-B2-A2 (рис.5).

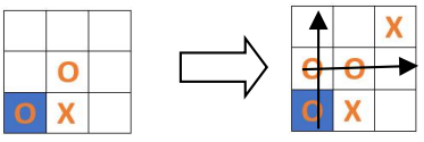
Рис. 5

Рассмотрим возможность выстраивания второй комбинации-ловушки, когда на ход первого игрока A3, противник отвечает ходом в угол C3. Первый игрок отвечает ходом A2, ставя второму игроку шах и вынуждая защищаться ходом A1. Противник радуется и угрожает шахом A1-C3, а первый игрок, защищаясь от шаха ходит B2 и играет комбинацию-ловушку A3-A2-B2 (рис.6).

Рис. 6

Третью комбинацию-ловушку можно разыграть, если в ответ на ход первого игрока в клетку A3, второй игрок ответит ходом C2. Первый игрок продолжает строить линию A3-B2, второй игрок вынужден закрываться C1, первый игрок получает шах и ходит C3, таким образом, формируя безвыходную комбинацию-ловушку A3-C3-B2 (рис.7).

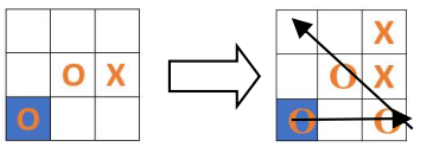
Рис. 7

Любую из этих трех комбинаций-ловушек можно разыгрывать из любой боковой клетки в симметричном варианте.

Можно сделать вывод, что любая угловая клетка (A1, A3, C1, C3) обладает большей атакующей способностью на старте, чем центральная B2 или боковая клетка (B1, C2, B3, A2).

Выводы. Изучив все комбинации-ловушки до начала партии и противодействия им, второй игрок имеет возможность как минимум вывести партию вничью.

Несмотря на то что ход в клетку B2 может казаться самым стратегически выгодным для начала партии, т. к. лежит на пересечении сразу 4 финальных линий, он таковым не является. Он открывает возможности для построения лишь одной беспроигрышной комбинации-ловушки B2-C1-C3 (или ее симметричных эквивалентов) и оставляет противнику целых 4 клетки для второго хода, чтобы вывести партию вничью.

Всего в игре «Крестики-нолики» существуют 4 основных типа комбинаций-ловушек (A1-B2-A3, A3-A2-B2, A3-B2-C2, A3-C3-C1 (рис.8)) и их симметричные эквиваленты.

Рис. 8

Практическое применение. Результаты данной работы имеют две области применения. Первая — наиболее понятная и осязаемая — это возможность применять описанные алгоритмы на практике, добиваться красивых побед, а при невозможности выигрыша, выводить ее вничью.

Вторая область применения полученных выводов представляется наиболее интересной и перспективной с научной точки зрения. Автор написал программу, которая просчитывает исход партии по ее первым двум ходам, при условии, что ни один из игроков не поддается противнику целенаправленно. Программа написана на языке программирования Python. Автор назвал ее «Крестики-нолики-444» (рабочее название «X/O-444») в честь математической школы 444, в которой он обучается. Код программы содержится в Приложении 1.

Следующим шагом на базе этого кода станет разработка игрока-робота, который никогда не будет проигрывать в крестики-нолики, а также, возможно, обучающей программы-приложения, которая наглядно визуализирует алгоритмы этого робота и дает выкладки максимально выигрышных игровых линий. Существующие реализованные аналоги будущего робота не дают беспроигрышный результат в 100 % случаев, поэтому автор ставит себе следующую задачу — создать непобедимого игрока-робота.

Заключение

Поставленная задача — написание уникального кода, который сможет определять исход партии игры в «Крестики-нолики» — решена в полном объеме. Написана программа «Крестики-нолики-444» («X/O-444»), которая прогнозирует исход партии в «Крестики-нолики» со 100-процентной точностью по ее первым двум ходам, при условии, что игроки целенаправленно не поддаются друг другу. В ходе работы над проектом удалось выполнить несколько промежуточных задач, как-то: изучить математику игрового поля и самой игры, разработать и систематизировать алгоритмы беспроигрышного ведения партии. Полученные результаты открывают поле для продолжения работы в данном направлении и их практического применения — разработке игрока-робота и робота-учителя.

Благодарности. Автор проекта выражает глубокую признательность всем педагогам 6-го математического класса математической школы ГБОУ «Школа № 444», которые ежедневно поддерживают интерес к математике и решению нестандартных задач красивыми и оригинальными способами. Также хочется выразить благодарность преподавателям «Инжинириума» при МГТУ им. Н. Э. Баумана — центру молодежного инновационного творчества и технопарку, где автор имеет возможность реализовывать на практике свои творческие решения. И особую благодарность я выражаю своим родителям, которые возят меня в лучшую школу и на лучшие кружки, чтобы поддерживать и развивать мои интересы.

Приложение 1. Программный код «X/O-444»

Литература:

1. Гарднер М. Математические головоломки и развлечения. — МИР, 1999. — 512c.
2. Гарднер М. Лучшие математические игры и головоломки. — АСТ, 2009. — 256с.
3. Перельман Я. И. Занимательная математика. — ТИОН, 2022. — 144с.
4. Еленьский Щ. По следам Пифагора. Сто исторических головоломок. — Качели, 2022. — 128c.
5. Аренс В. Математические игры. Центрполиграф, 2018. — 159с.