В данной научной статье описаны результаты изучения случайных процессов, их видов и свойств, которые составляют важную ветвь теории вероятностей и математической статистики, представляющие интерес не только с научной точки зрения, но и с социальной.

В теории случайных процессов в последние годы исследуется ряд процессов, основанных на результатах суммы случайных величин. Например, геометрический, процесс Паскаля и т. д. [2, 3, 4] Одним из таких случайных процессов является равномерный случайный процесс, т. е.

,

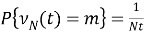
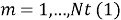
С этого момента мы будем ограничены использованием термина случайного процесса, вместо термина равномерный случайного процесса. Расчеты показывают, что — первый момент случайного процесса или математическое ожидание, дисперсия и корреляционная функция имеют вид [5]

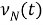
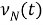
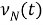
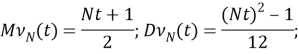
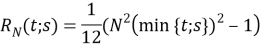
Теперь представим обобщение этого процесса. Если —взаимонезависимые равномерно распределенные случайные величины, для которых математические ожидания равны , а дисперсии , то

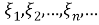
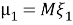
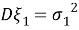
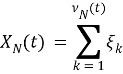
Этот процесс называется обобщенным равномерным случайным процессом. Учитывая характеристики второго порядка процесса , отсюда получаем

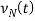
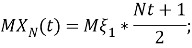
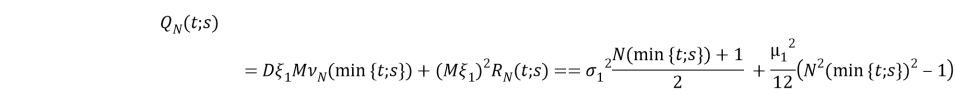
Где

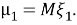
В случае N → ∞ находим последовательность неслучайных вещественных функций и , удовлетворяющих следующим условиям в качестве нормирующих последовательностей для нахождения предельных процессов этих процессов:

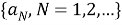
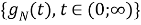
1) Для всех и имеется , , , и такая константа

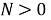
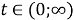
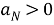
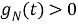
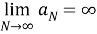
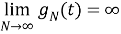
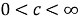
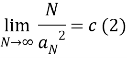
Существует такая ограниченная, положительная, вещественная, случайная функция , для

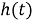
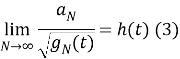
Посмотрим на такие случайные процессы,

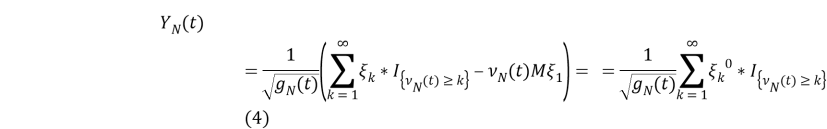
Совместное характеристическое функции этих случайных процессов будут иметь вид

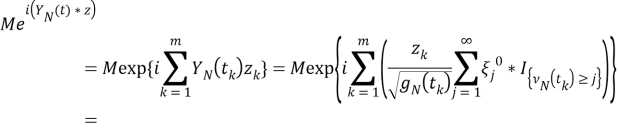
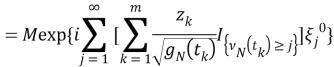
Здесь, используя условное математическое ожидание, а также свойства характеристической функции случайной величины, можно получить следующее,

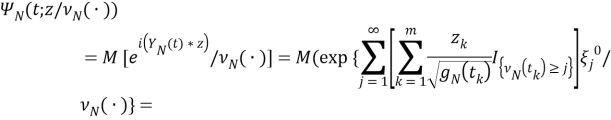
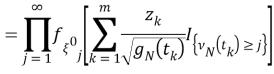
или здесь,

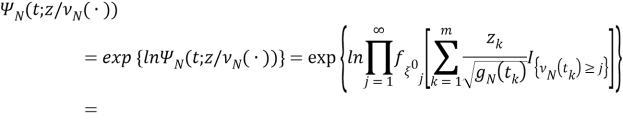
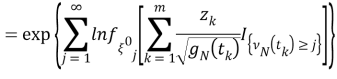
Так как то при z понятно, что приблие справедлив. Получаем, когда

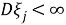
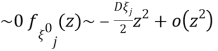
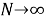
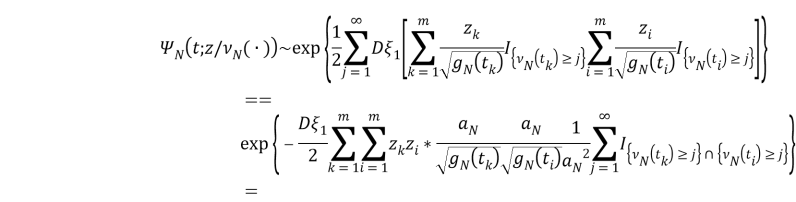
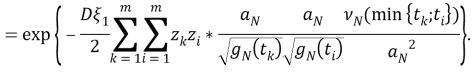
Если здесь использовать уравнения (2) и (3), тогда

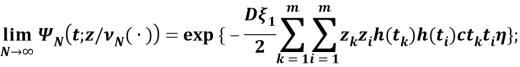
или же

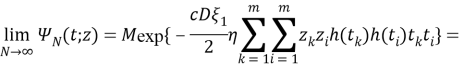
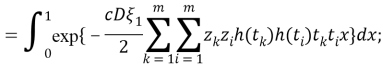
Здесь введем обозначение

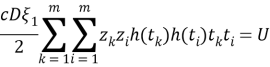
и находим значение интеграла по х,

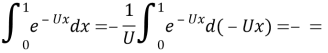
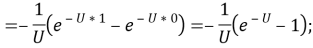
Мы возьмем значение U, подставив его в последнее уравнение

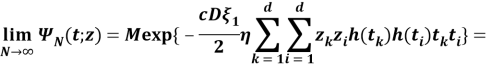
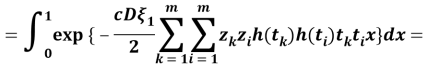
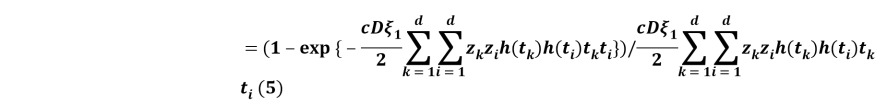
Полученные результаты . Теорема. В конечномерные распределении случайных процессов в случае сходится в конечномерное распределение случайных процессов которое характеристическая функция определяется уравнением (5). Если функция удовлетворяет условию Липшиса, то такая сходимость слабая.

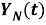
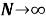
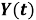
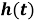
Литература:

1. Гурбангулы Бердымухаммедов. Знание — это счастье, вдохновение, процветание. -А: Туркменское государственное издательство, 2014.

2. Гихман И. И., Скороход А. В., Введение в теорию случайных процессов. М.: «Наука», 1977г.

3. Петров В. В. Суммы независимых случайных величин.–М.: Наука, 2006

4. Петров В. В. Предельные теоремы для сумм независимых случайных величин. —М.: Наука, 2007

5. Мередов Б. Исследования по теории суммирования случайных величин по Абелю. Диссертация на соискания учёной степени кандидата физико-математических наук, — Ашгабат: 1978.