Данная статья направлена на генерирование случайных чисел с равномерным распределением по ординатами звуковой карты.

Ключевые слова: случайные числа, аппаратный генератор чисел, преобразования Джонсона.

В современной информатике широко используются случайные числа в самых разных приложениях — от криптографии до развлечений. При этом от качества используемых аппаратными генераторов случайных чисел (АГСЧ) напрямую зависит качество получаемых результатов. В АГСЧ должен генерировать абсолютно случайную последовательность чисел. Такую последовательность можно получить если использовать шум со звуковой карты.

Проблема, связанная с АГСЧ, — это смещение последовательности выходных битов (когда одних цифр в последовательности больше, чем других, например единиц больше, чем нулей в двоичной системе). Она вызвана особенностями физических процессов, используемых в генераторах шума. Данная проблема может быть решаема с помощью специальных математических моделей, которые позволяют получить последовательность случайных чисел заданным распределением, в частности, равномерным. Для решение данной проблемы было использовано математической модели суть которого заключается в следующем. Аппаратные датчики получают последовательность значений случайной величины с произвольным распределением, по которой находят преобразования Джонсона определенной семьи. Дальше найденным преобразованием Джонсона значение случайной величины с произвольным распределением превращают в значение гауссовской случайной величины, по которым получают случайны числа СЧ с равномерным законом распределения используя обратное преобразование Джонсона из семьи S_b. [1]

Поэтому возникает необходимость в усовершенствованные математической модели, которая позволит получить последовательность СЧ заданным распределением, в частности, равномерным. Цель данной работы заключается в том, чтобы усовершенствовать предложенную модель для формирования ВЧ с равномерным распределением по значениям случайной величины с произвольным распределением для аудио карты Realtek ALC269. В работе была усовершенствована математическая модель, для звуковой карты Realtek ALC269, показало работоспособность данной математической модели [2].

Теоретическое решение. В работе было применено преобразование Джонсона из семьи S_B. Также было получено 4420 значений с звуковой карты.

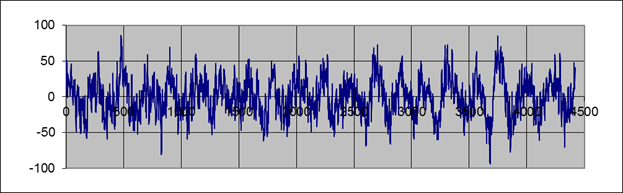
Рис. 1. Значение случайной величины x

В общем случае преобразования Джонсона выглядит

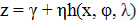, (1)

где z — нормированная нормально распределенная случайная величина с нулевым математическою надеждою и единичной дисперсией: x- случайна величина, нормализуется; "γ", "η", "φ", "λ" — параметры преобразования Джонсона, "η"> 0, -∞ <γ <∞, "λ"> 0, -∞ <"φ" <∞; h — функция с определенной семьи;

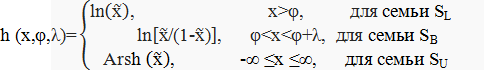
тут 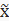 = (х — φ) / 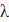; Arsh(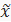) = ln(),

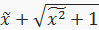Обратное к превращению определяется как

x = 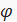+ 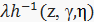, (2)

де 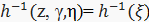; ξ = (z — γ)/η;

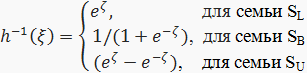
Выбор определенной семьи преобразования Джонсона осуществляют по оценкам асимметрии А в квадрате и эксцесса ε (рис. 2).

Рис. 2. Комбинации А² и ε для выбора определенной семьи

В параметры преобразования предложено находить в результате решения задачи

θ=arg min{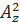+(ε_z — 3)²}, (3)

где θ — вектор неизвестных параметров преобразования,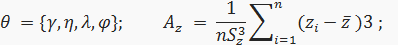

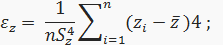
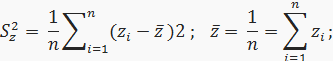
zi — и-то значение нормализованной случайной величины z в выборке длиной n, и ε [1, n], определяется за.

Значение случайной величины u с равномерным законом распределения на интервалов [-1, + 1] получают по значениям гауссовской случайной величины z с нулевым математическим ожиданием и одиночной дисперсией используя обратное преобразование Джонсона из семьи S_B

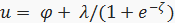, (4)

де ζ = (z — γ)/η;

γ = 0,56228; η = 3,59566; φ = -0,005348; λ = 0,01158.

Значение гауссовской случайной величины z формируют следующим образом. По АД (или иным образом) получают последовательность значений случайной величины x с произвольным распределением по которой находят преобразования Джонсона определенной семьи. Параметры этого преобразования определяют по решению задачи. Дальше найденным преобразованием значение случайной величины x с произвольным распределением превращают в значение гауссовской случайной величины z.

В качестве значений случайной величины x можно взять и ординаты случайного процесса. Например, известно, что ординаты речевого сигнала можно нормализовать с помощью преобразования Джонсона из семьи S_u. Только нужно, чтобы случайный процесс, ординаты которого берутся в якоcти значений случайной величины x, имел малое время корреляции. Практические результаты. Для проверки работоспособности предложенной математической для формирования ВЧ с равномерным распределением по значениям случайной величины с произвольным распределением было выполнено преобразование последовательности значений гауссовской случайной величины z с нулевым математическим ожиданием и единичной дисперсией, которые приведены на рис.3, в значение случайной величины u с равномерным законом распределения на интервале [-1, + 1] используя формулу (4).

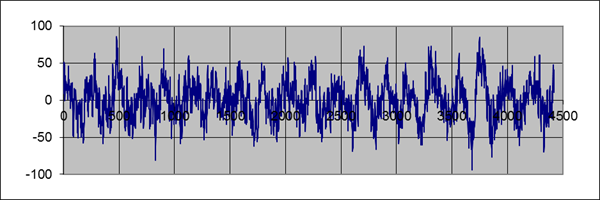
Рис. 3. Значение случайной величины z

Значение случайной величины u с равномерным законом распределения приведены на рис. 4.

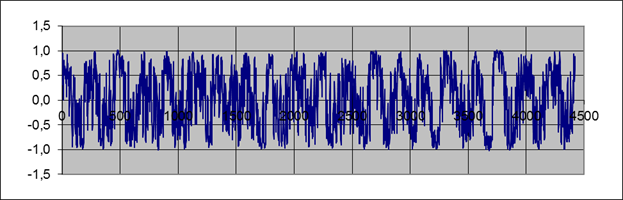
Рис. 4. Значение случайной величины u с равномерным законом распределения

Литература:

1.                  Приходько С. Б. Використання перетворення Джонсона для отримання випадкових чисел з рівномірним розподілом за значеннями випадкової величини з довільним розподілом [Текст] / C. Б. Приходько // Системи обробки інформації. — 2012. — Вип. 4 (102), Т.2. — С.128–130.

2.                  Приходько С. Б., Решетняк В.В Удосконалення математичної моделі для створення послідовних випадкових чисел з рівномірним розподілом. [Тезис] / Приходько С. Б., Решетняк В.В // Сучасні проблеми інформаційної безпеки на транспорті. — 2014. С. 63–64.