В данной статье рассмотрено приложение теории случайных процессов в экономике для регулирования оптимального объема спроса и предложения энергоснабжения.

Ключевые слова: случайный процесс, спрос и предложение, гармоника, энергоснабжение.

Объем спроса электроэнергии представляет от себя некоторый случайный процесс. Реализация этого случайного процесса является детерминированной функцией. Как известно, случайный процесс можно представить в виде спектрального разложения, каждая составляющая которого представляет собой гармоническую функцию (или гармонический процесс) [1].

В работе рассматривается гармоническая составляющая функции спроса объема электроэнергии, которая в общем виде задается по формуле:

F(x) =Asin (x + ) (1)

где A — амплитуда гармоники, - частота гармоники, - начальная фаза.

В реальных процессах характеристики гармоники А, , являются случайными величинами. В работе будем рассматривать их реализации, т. е. случай, когда функция (1) является детерминированной.

Уровень предложения электроэнергии пусть задается некоторой детерминированной функцией — f(x), в частности может быть постоянной.

Для управления процессом регулирования объема спроса и предложения электроэнергии как качественная характеристика рассматривается разность функций F(x)-f(x) в некотором исследуемом интервале.

В простом случае пусть объем предложения электроэнергии постоянен, т. е. f(x)=H, где H — известный уровень объема предложения.

Тогда графически процесс обеспечения электроэнергией при постоянном уровне предложения (H), можно представить в следующем виде (на рисунке представлена функция (1) при A=2, =1, =2.3 и H=1):

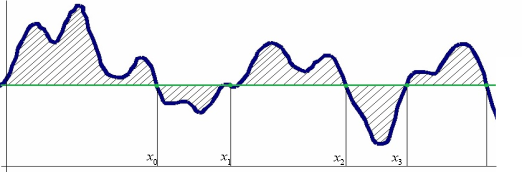
Рис. 1

А когда объем спроса от себя представляет некоторую заданную функцию (в частности, можно рассматривать многочлен некоторой степени), то графически процесс обеспечения электроэнергией имеет следующий вид:

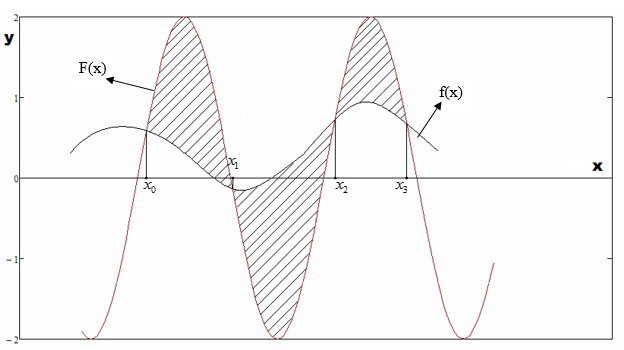
Рис. 2.

Для регулирования объемами спроса и предложения введем следующие определения:

а) площади плоских фигур, сверху ограниченных линией F(x), снизу f(x), когда

, будем называть объемами избыточного предложения;

б) площадь подобной плоской фигуры, сверху ограниченной линией f(x), а снизу F(x), когда , будем называть объемом дефицита спроса.

Постановка задачи.

Для оптимального управления процессом спрос-предложение в заданном промежутке времени в работе предлагается выбрать следующие критерии:

1) чтобы суммарные площади типа (а) накрыли суммарные площади типа (б);

2) а разности этих площадей были минимальны.

Решение задачи.

Данная задача в общем случае сложная. Сложность обусловлена выбором абсцисс точек пересечения — [3]. В работе предлагается решить задачу двумя этапами.

Этап I. Найти оптимальное решение, когда уровень предложения постоянный, т. е. найти оптимальный уровень предложения(H*) для заданного спроса и определить абсциссы точек пересечения (см. рис. 1):

. (2)

Этап II. Для улучшения оптимального распределения спроса и предложения электроэнергии авторами предлагается выбрать уровень предложения для рассматриваемого интервала как многочлен не более чем 3-й степени, проходящий через определенные точки (2).

В работе решение задачи реализовано алгоритмическим путем.

Для решения первого этапа задачи предлагается следующий алгоритм:

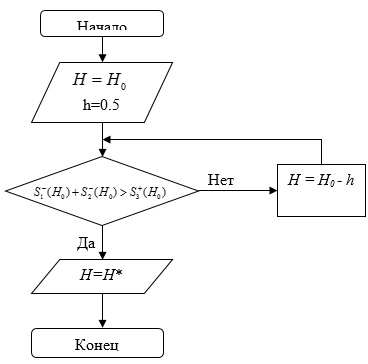
В алгоритме площади типа (а) и (б) вычисляются по формулам:

; ;

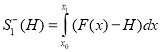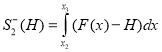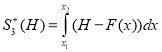
Второй этап. По полученным точкам уровень предложения «поправляем» многочленом Лагранжа не более чем 3-го порядка [2]:

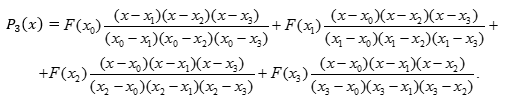
Для сравнения эффективности площади выбросов [3] будем вычислять по формулам:

; ;

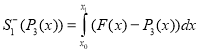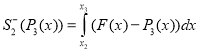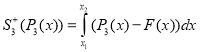
и как критерий улучшения эффективности предлагается следующий функционал:

В общем случае условия выполнения функционала аналитическим образом трудно реализуемы.

В работе алгоритмическим путем реализована поставленная задача, когда уровень спроса представляется как гармоническая функция F(x)= Asin ().

Вывод:

Когда постоянный уровень предложения при заданном спросе заменяется многочленом Лагранжа, то получается более точное распределение спроса и предложения электроэнергии.

Предложенный оптимизационный алгоритм реализации распределения спроса и предложения можно применять для решений разных инженерных задач.

Литература:

1. Вентцель Е. С., Овчаров Л. А. Теория случайных процессов и её инженерные приложения. — Учеб. пособие для вузов. — 2-е изд., стер. — М.: Высш. шк., 2000. — 383с.: ил
2. Пискунов Л. С. Дифференциальное и интегральное исчисления: Учеб. для вузов. В 2-х т. Т. I: — М: Интеграл-Пресс, 2001. — 416 с.
3. Тихонов В. И., Хименко В. И. Выбросы траекторий случайных процессов. М.: Наука, 1987г.
4. Томас Кормен, Чарльз Лейзерсон, Рональд Ривест, Клиффорд Штайн. Алгоритмы. Построение и анализ. — 1-е изд, М.: Вильямс, 2005. — 1296 с.