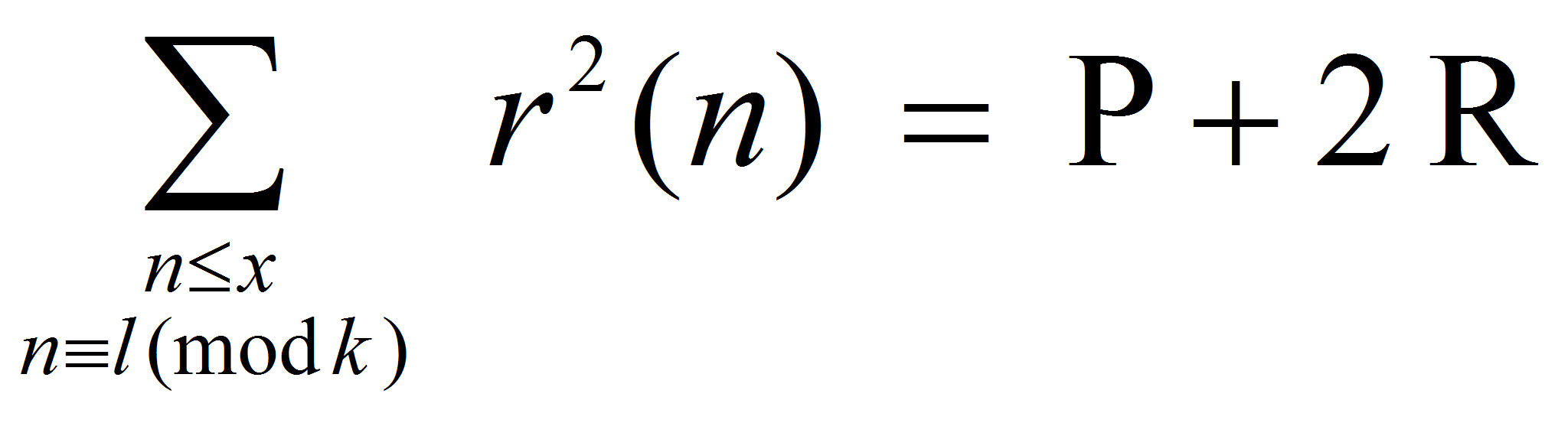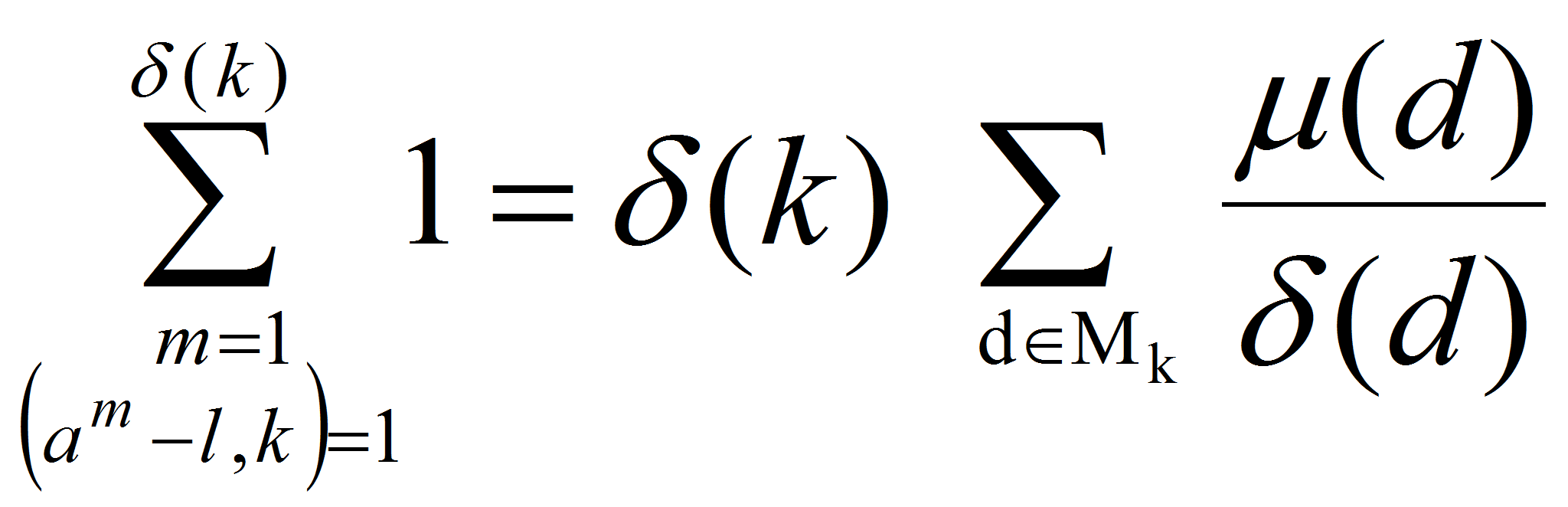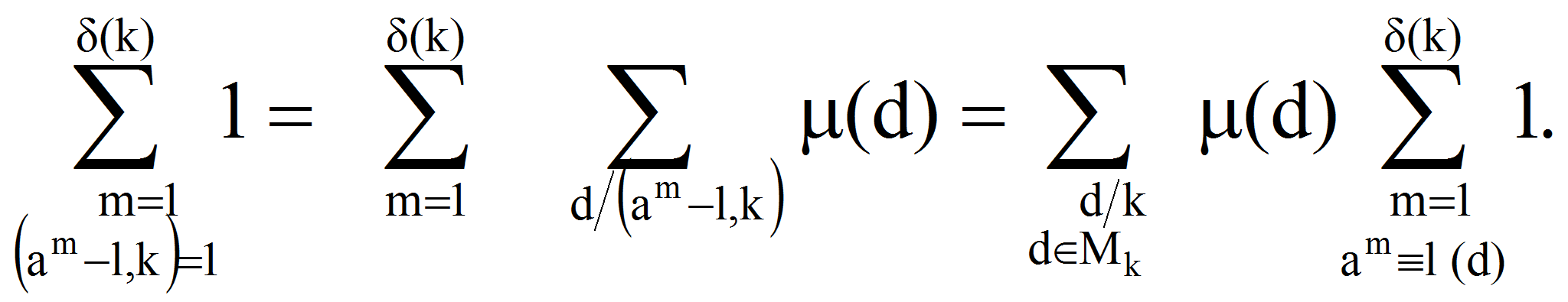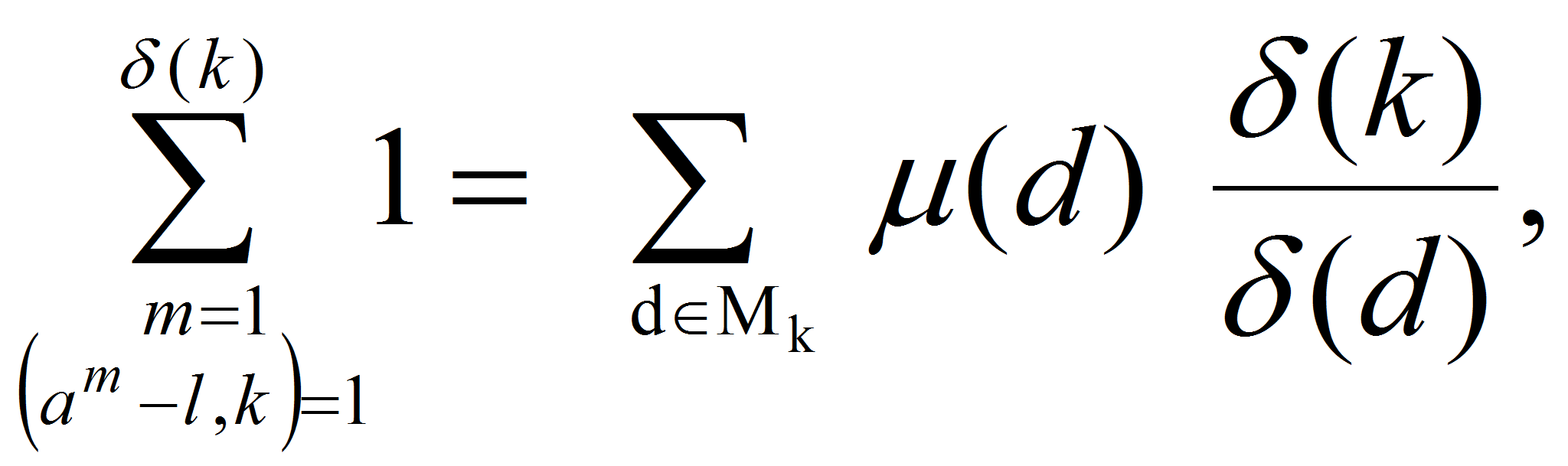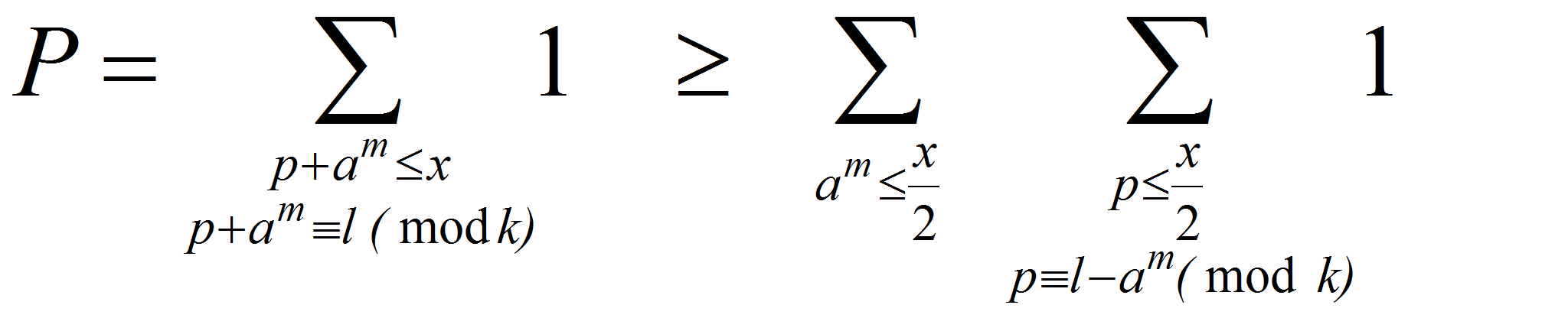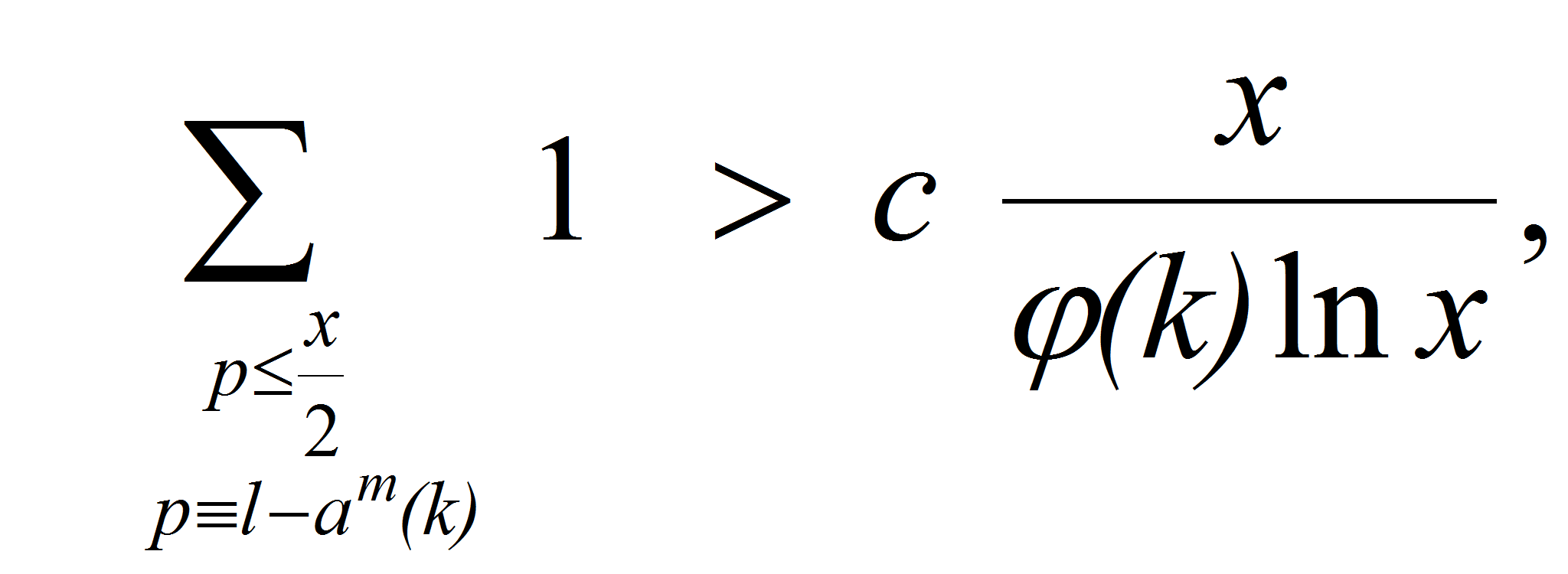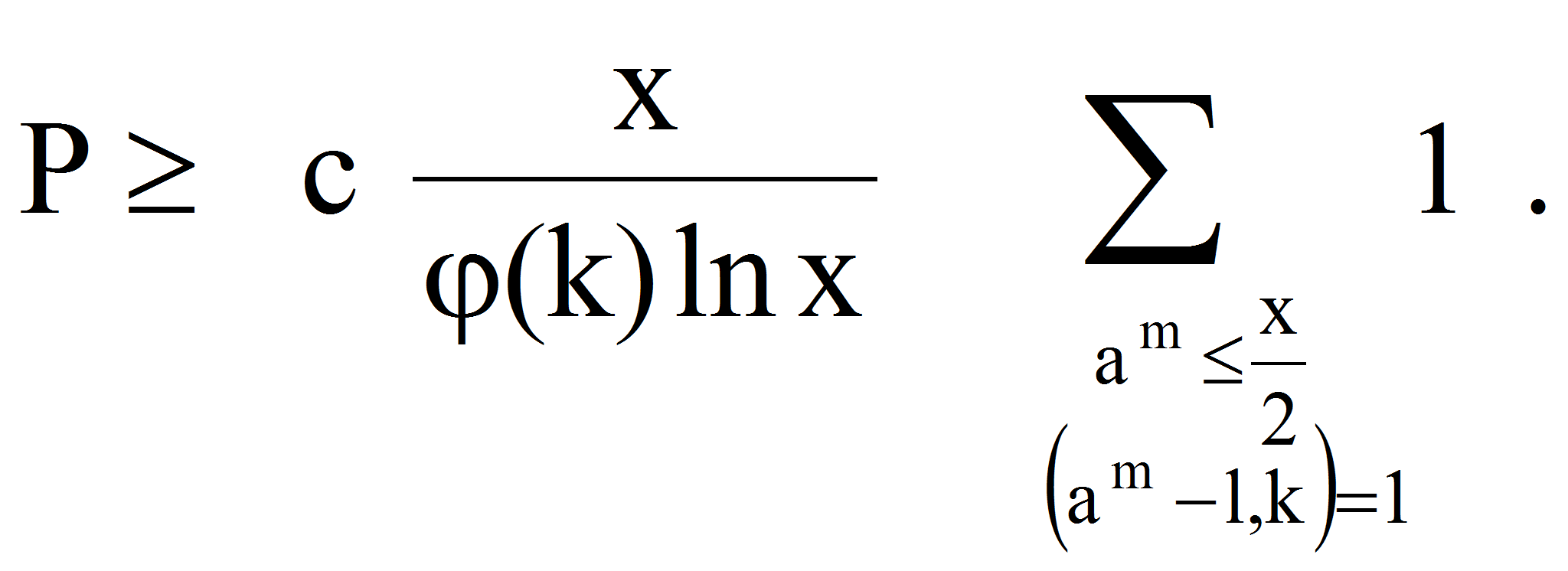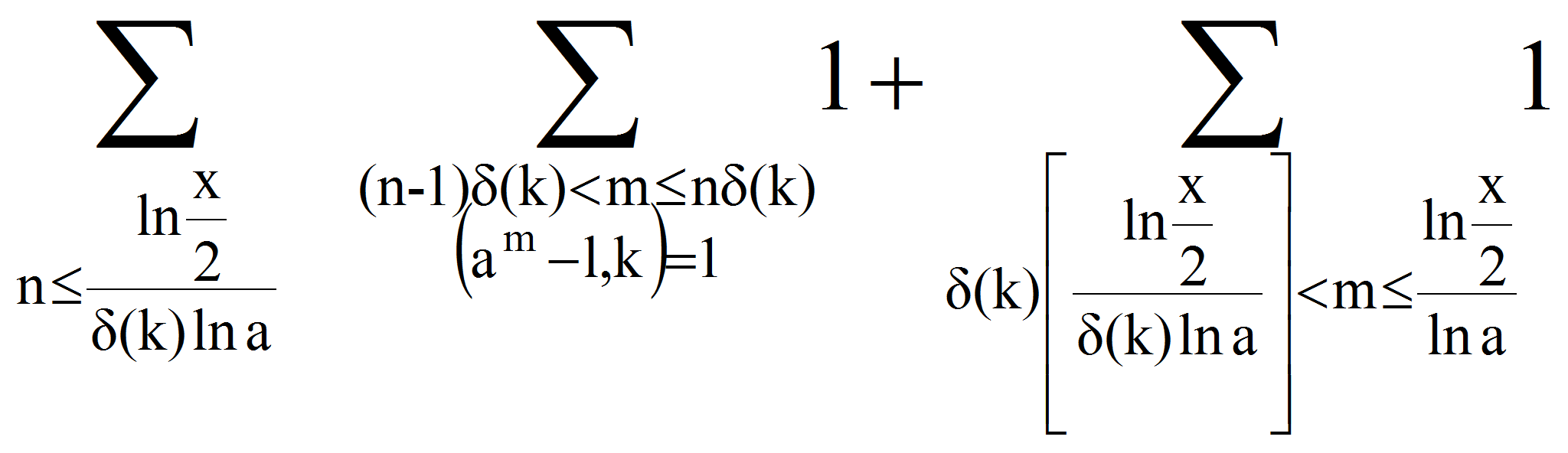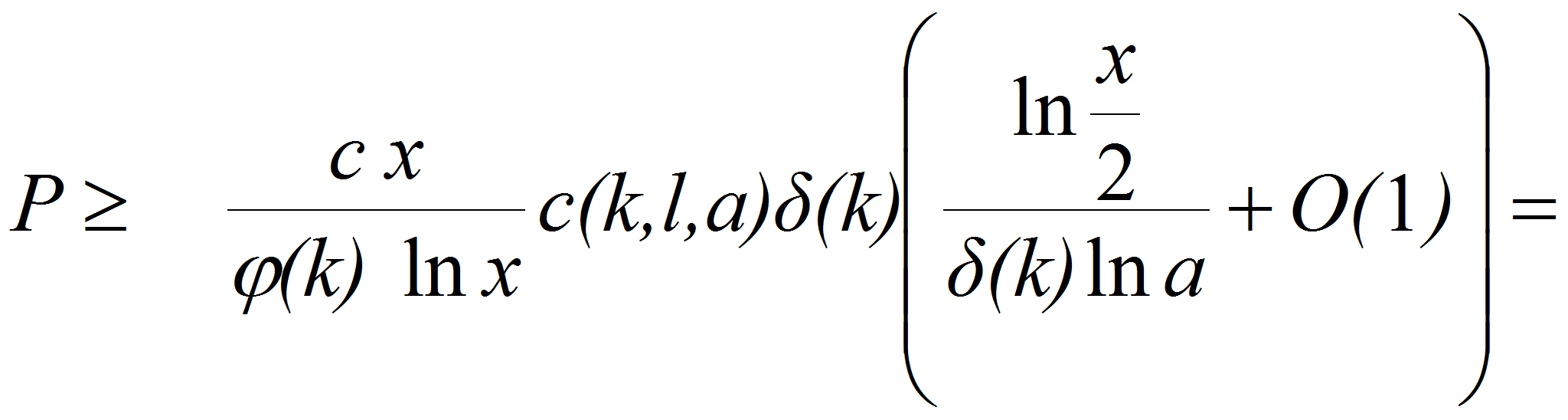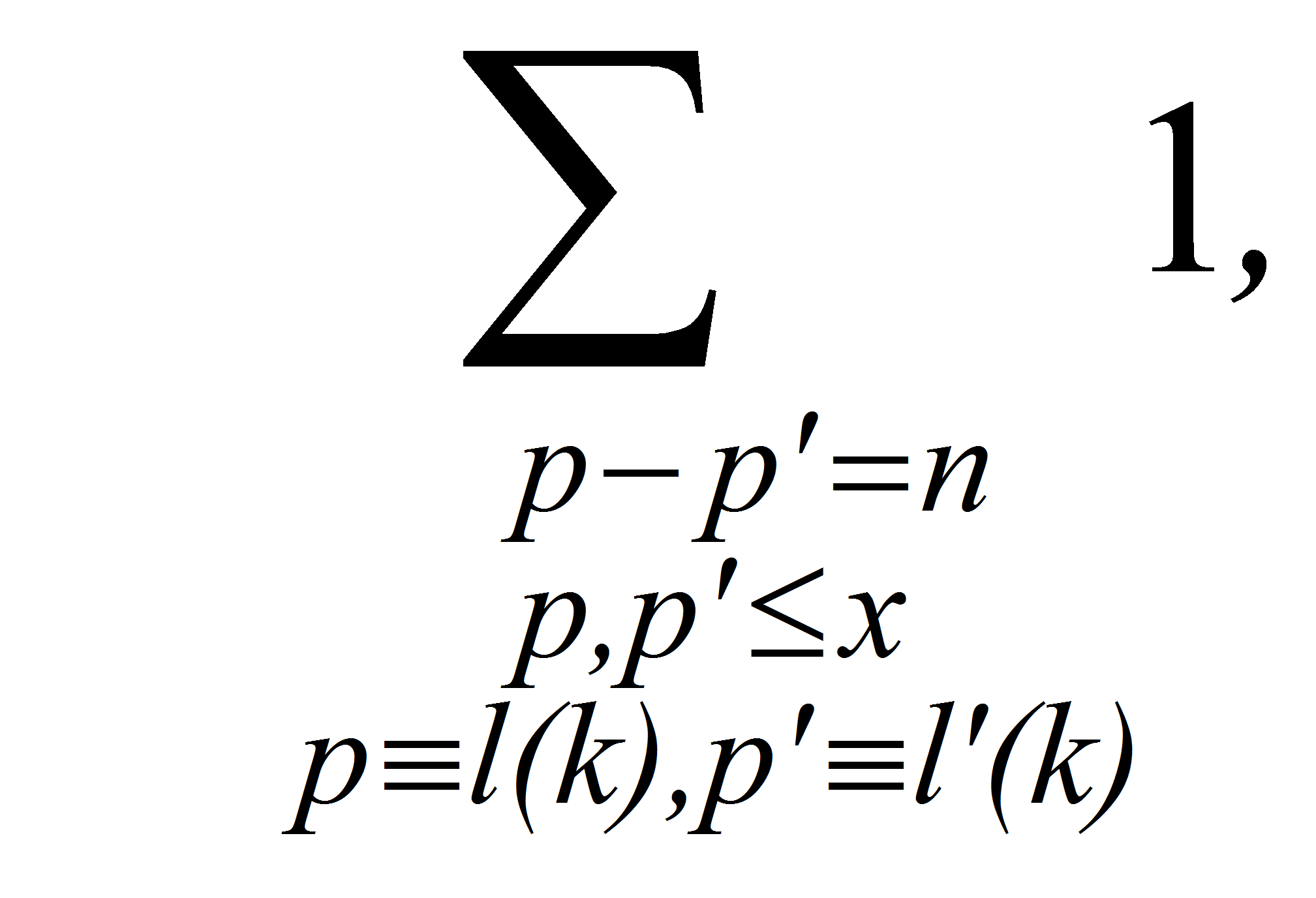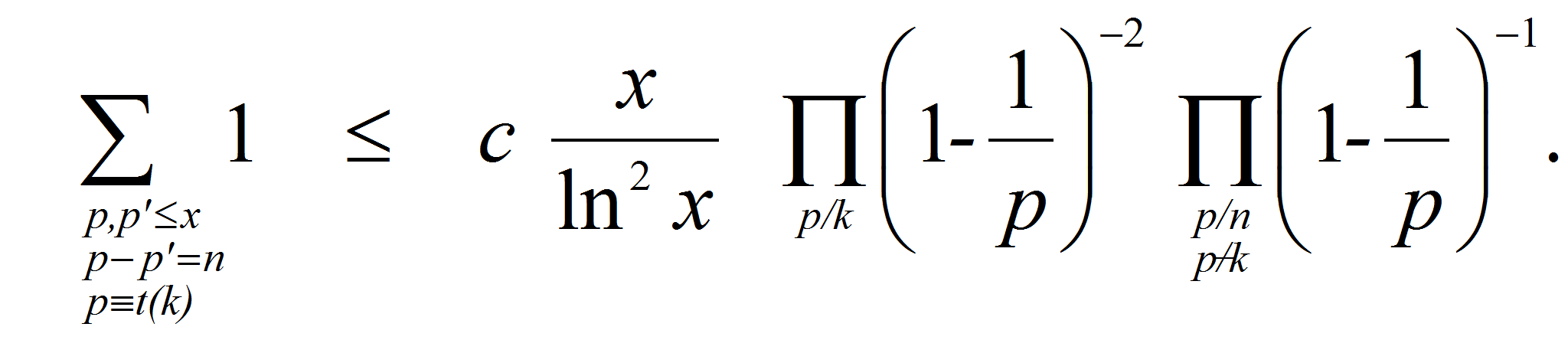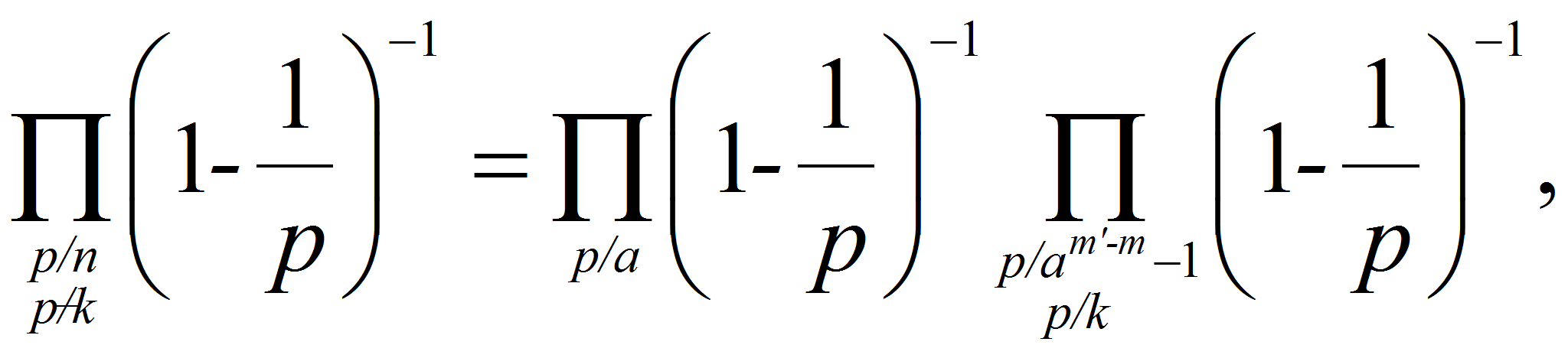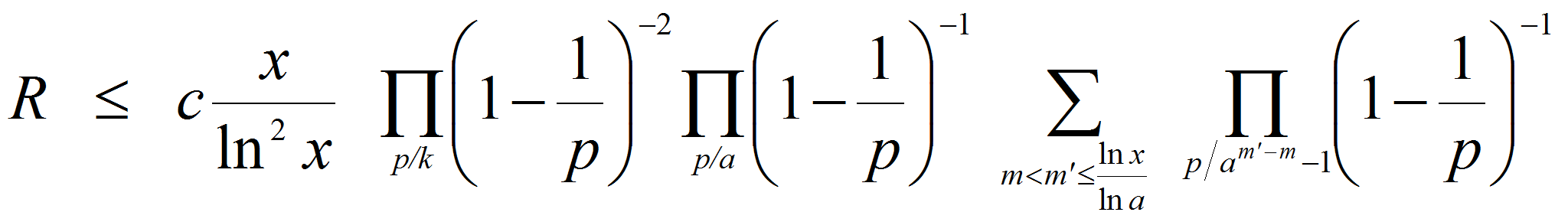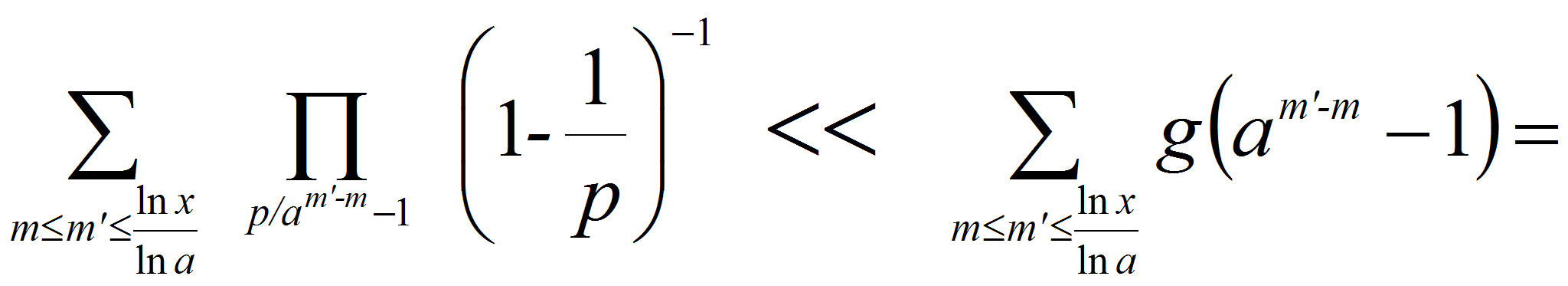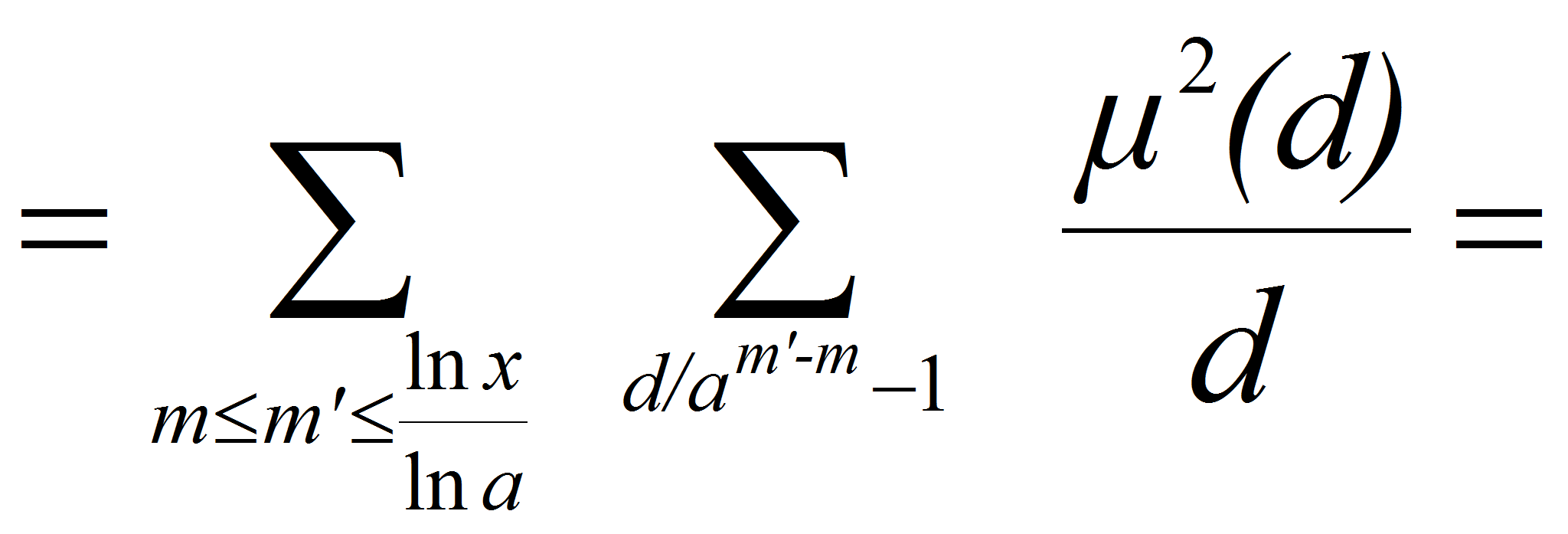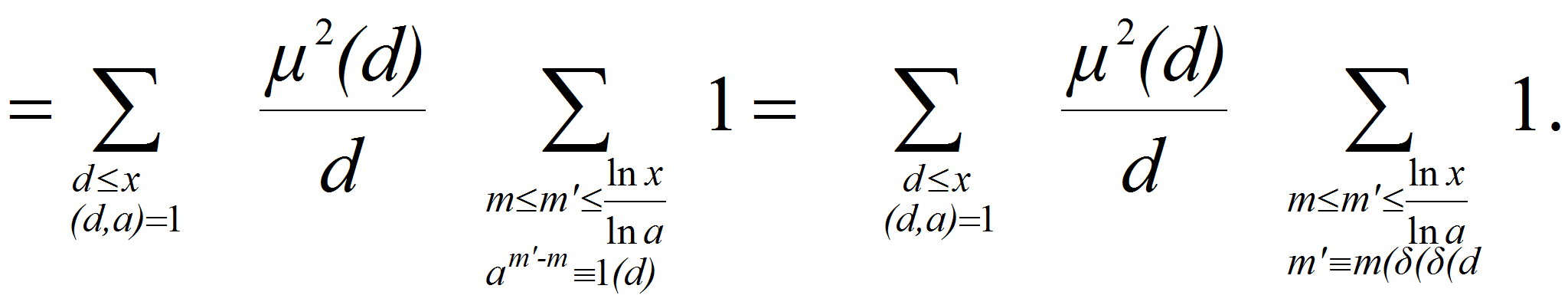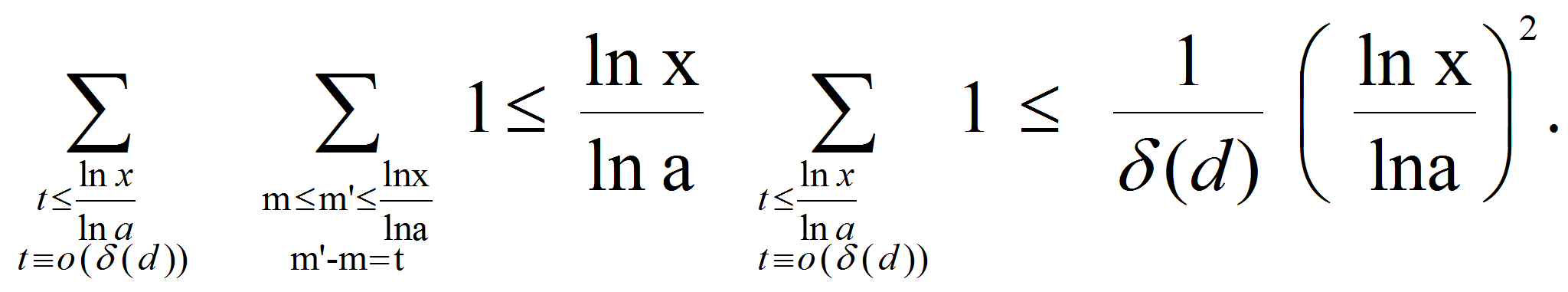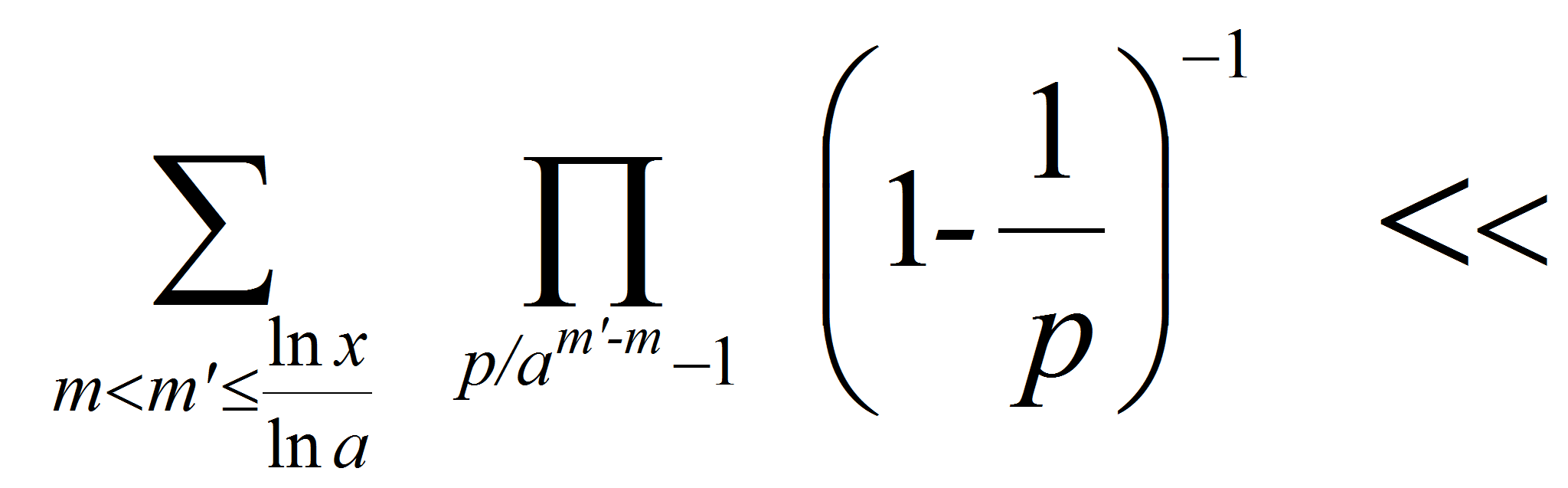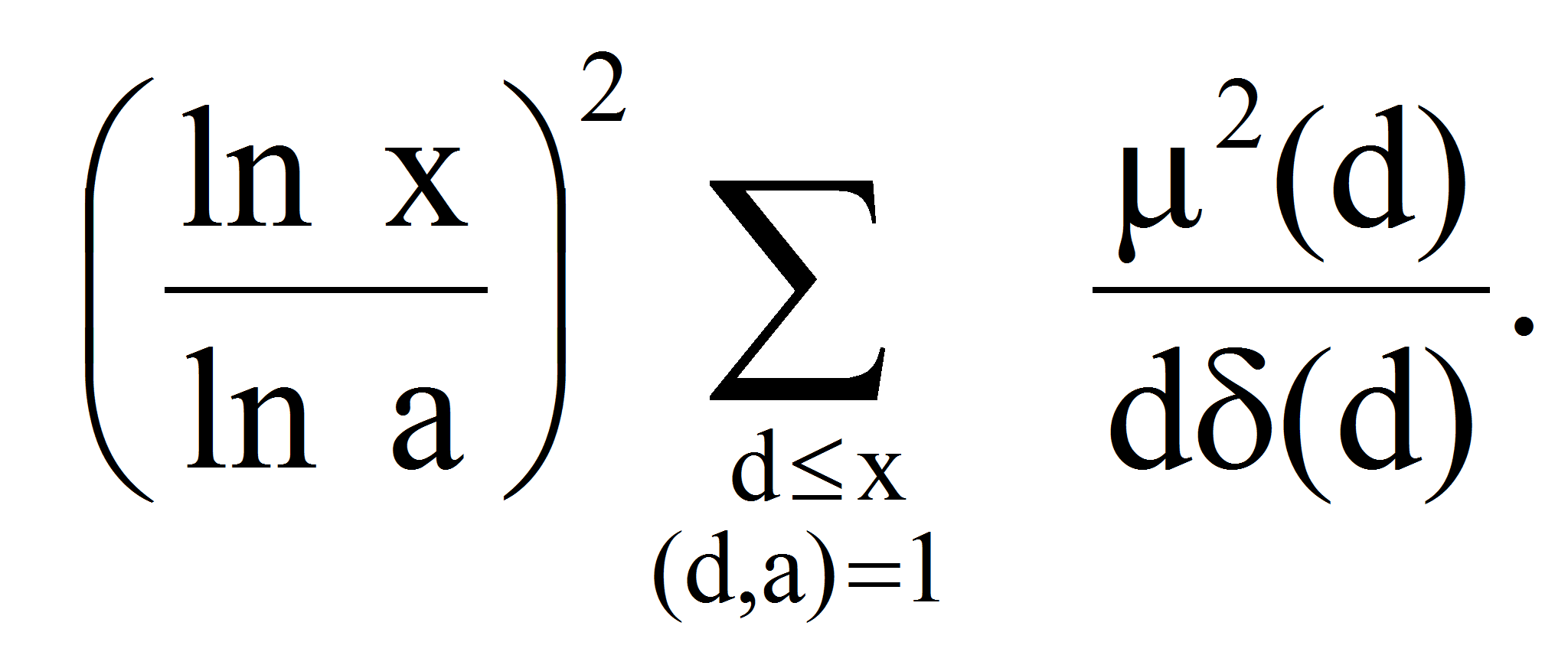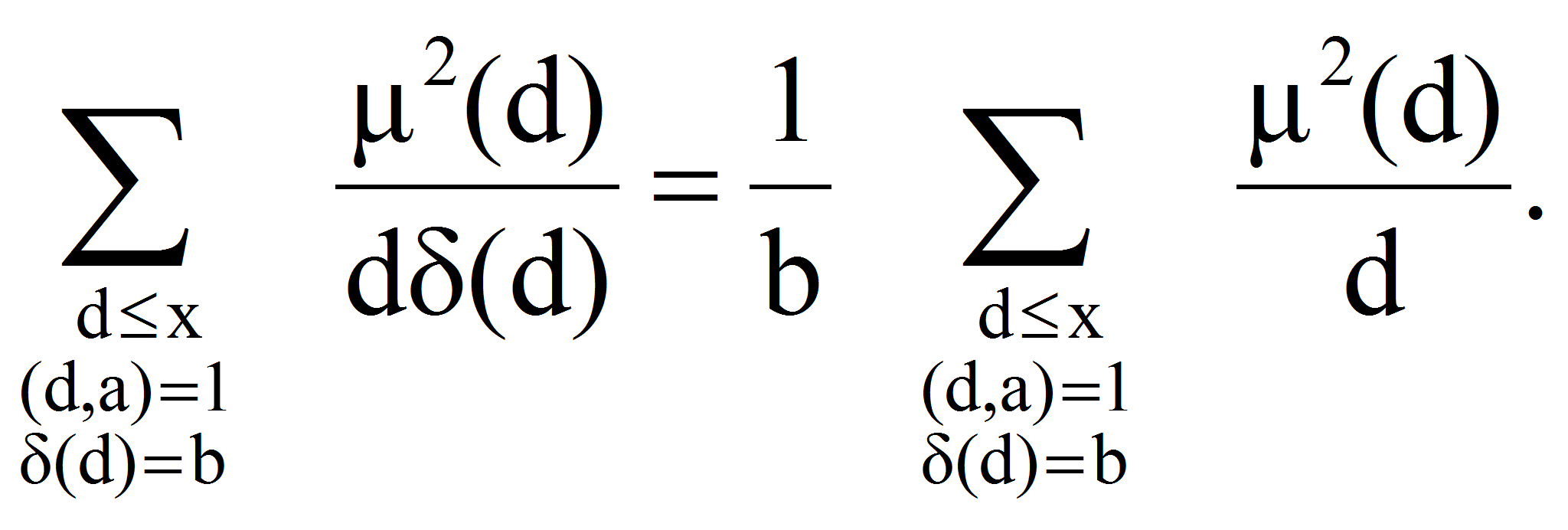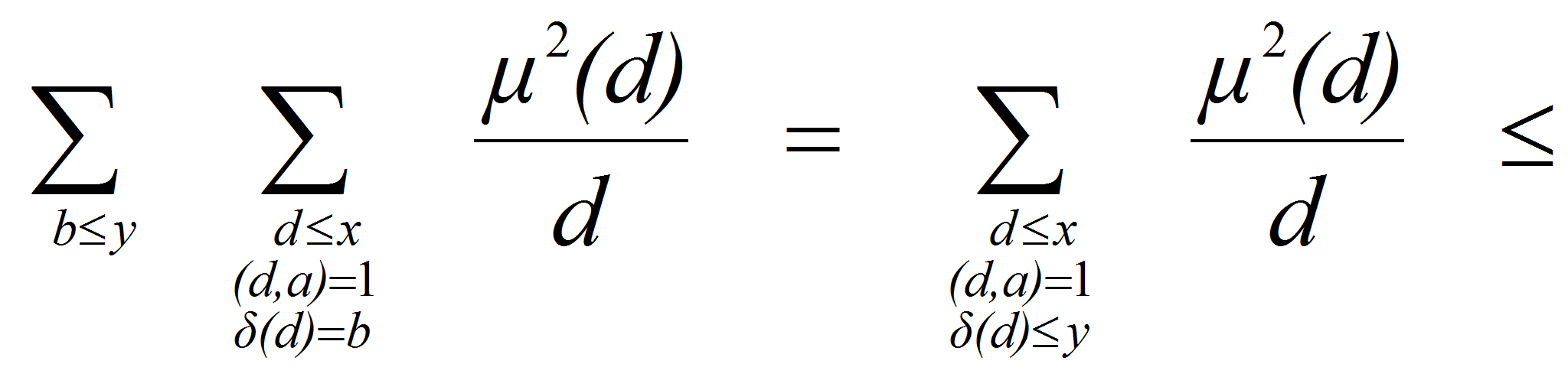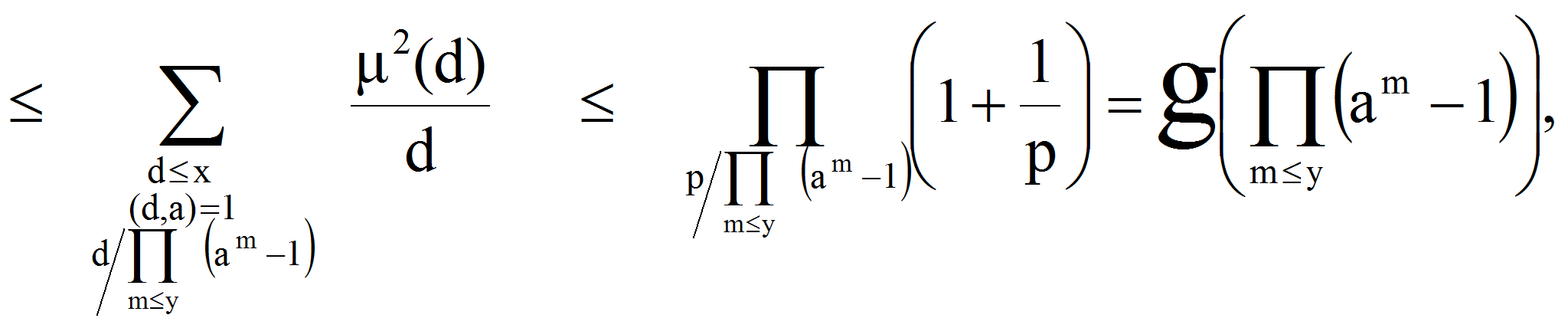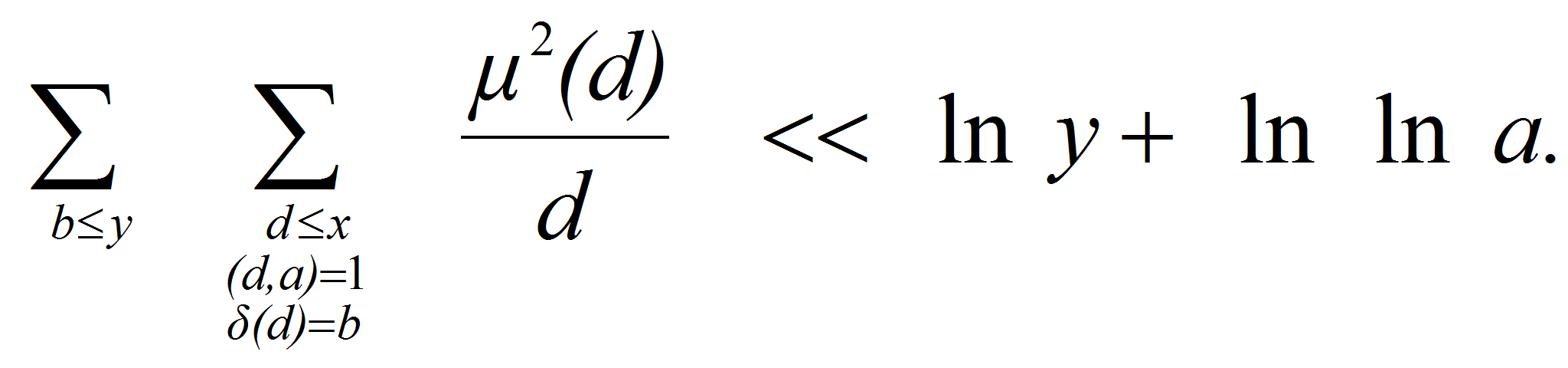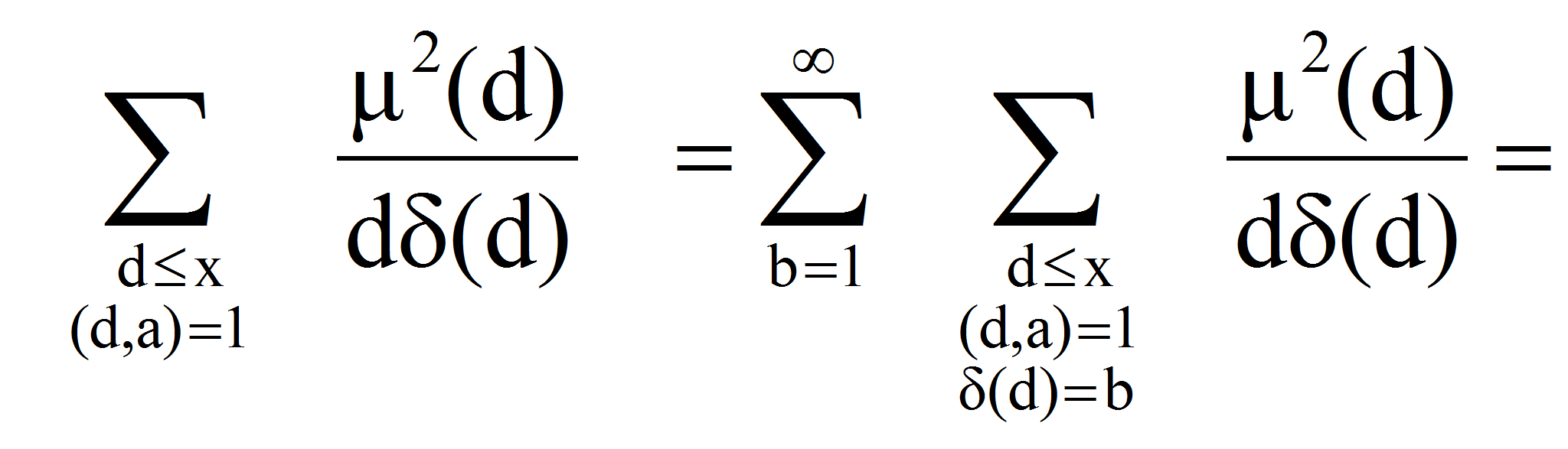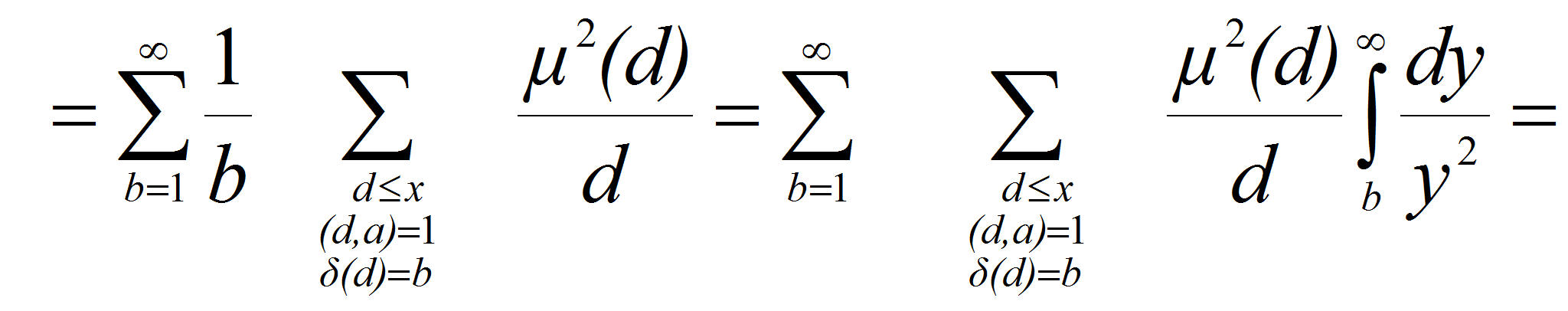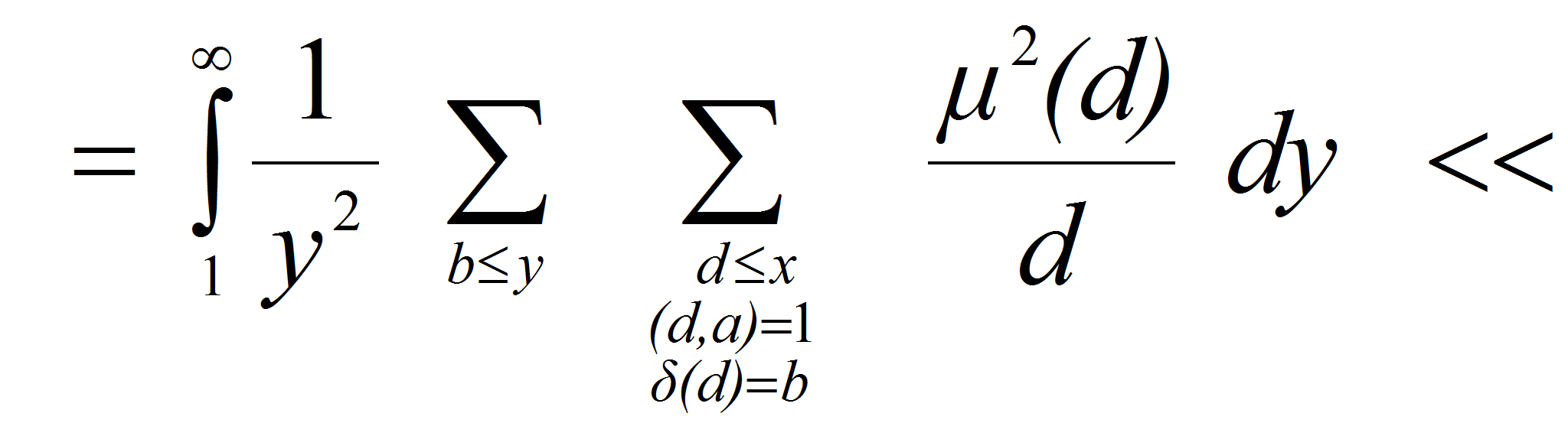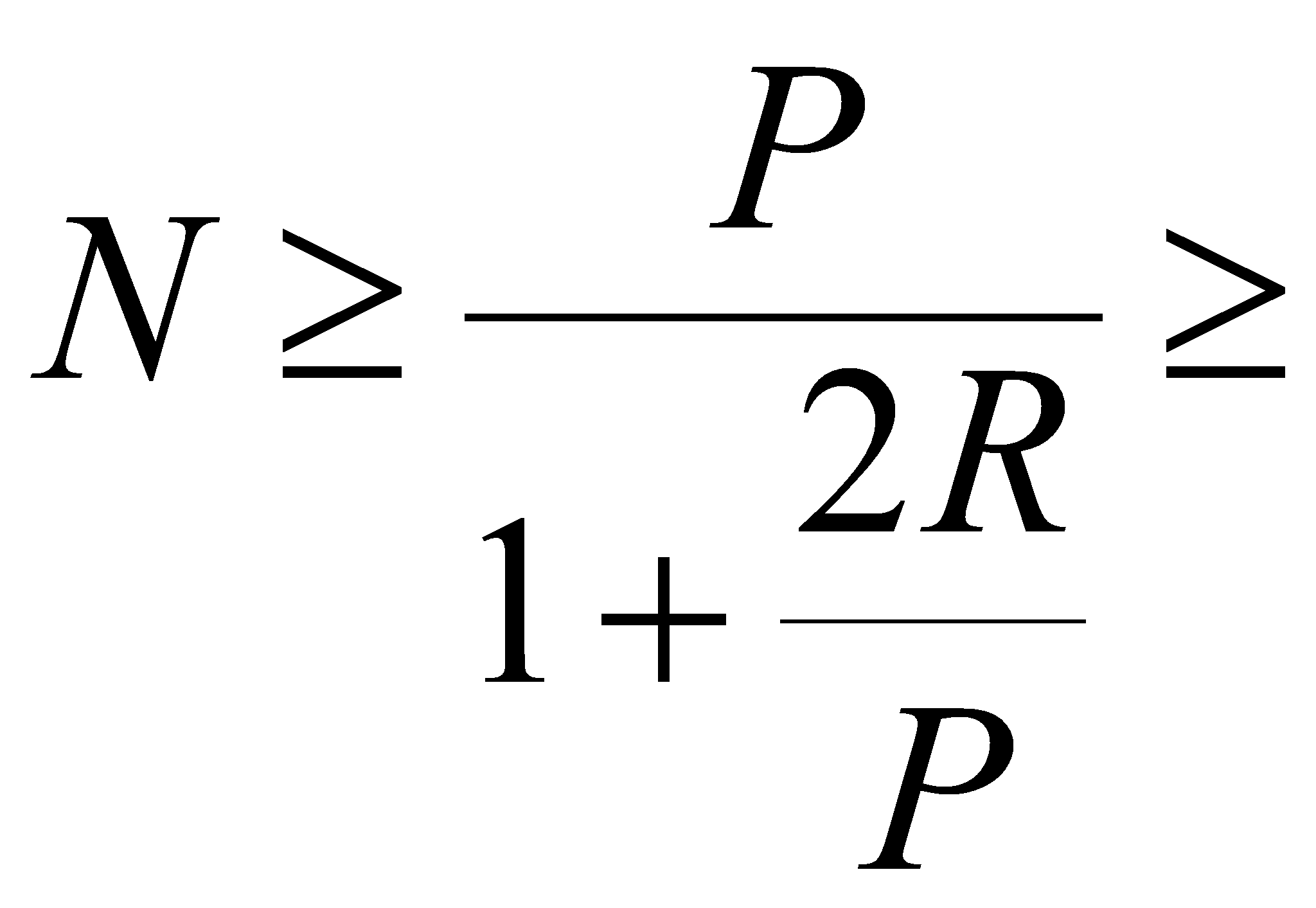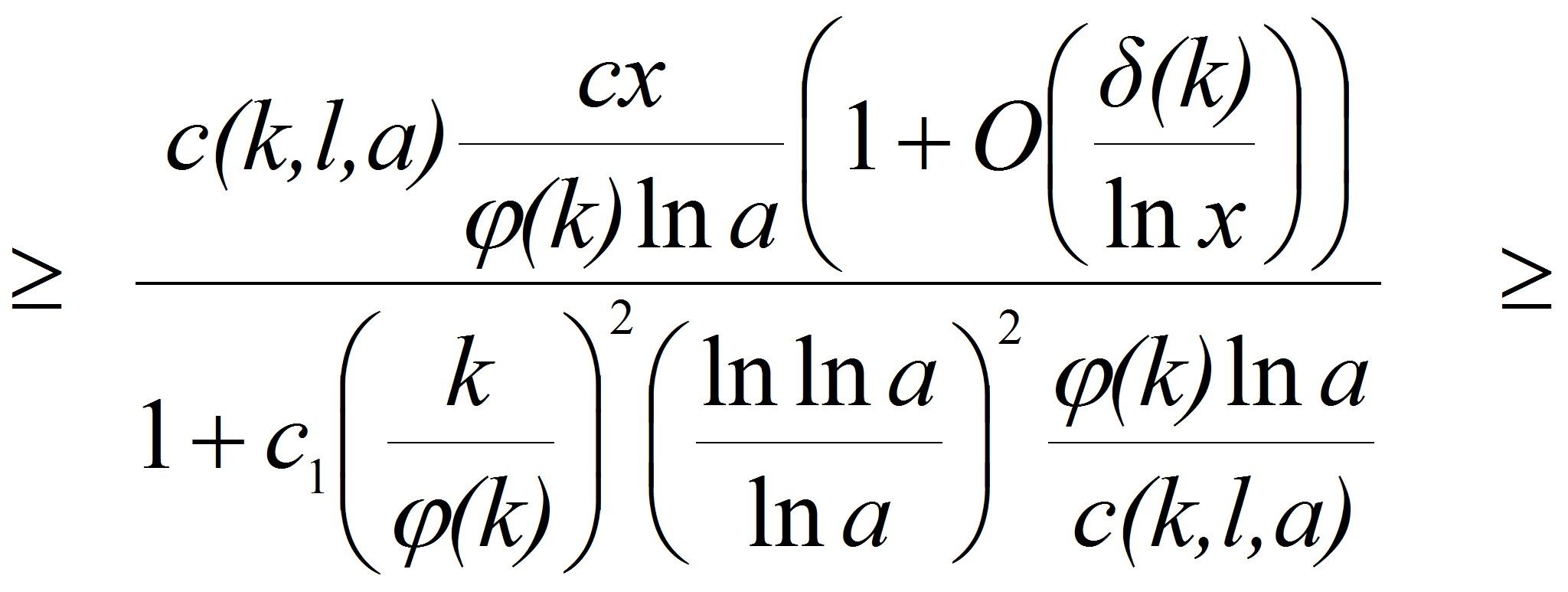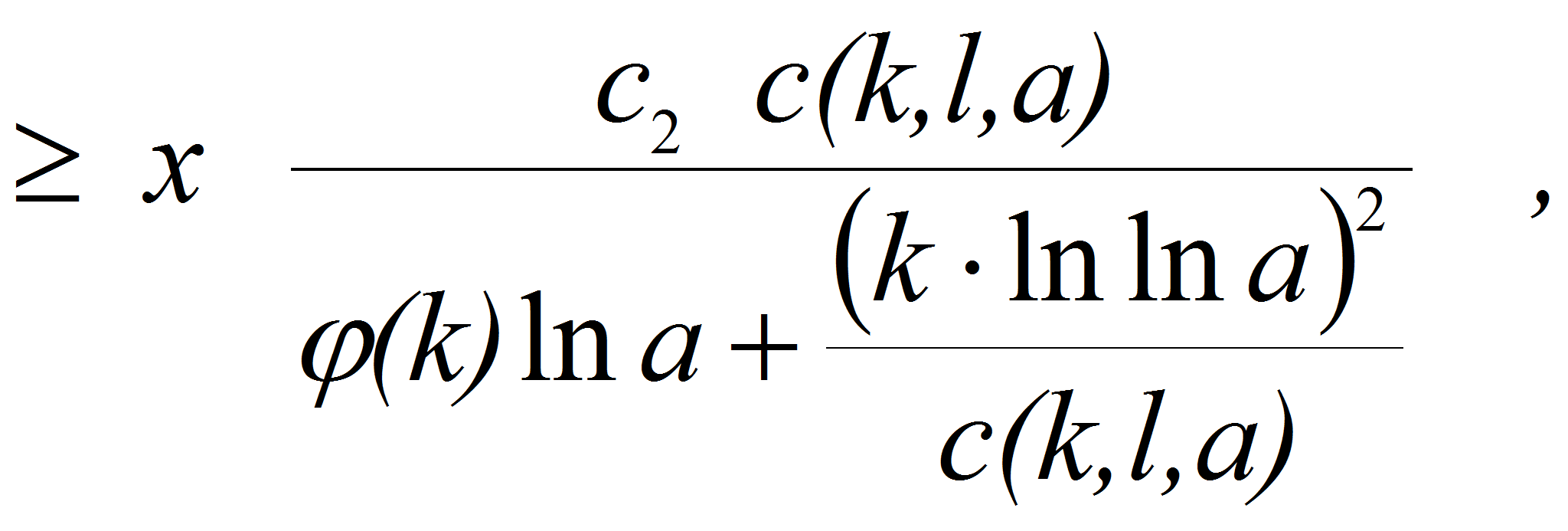В работе рассматривается задача о распределении натуральных чисел, принадлежащих заданному классу вычетов по некоторому модулю и представимых в виде суммы u+v, где u,v- члены двух заданных последовательностей натуральных чисел. Получены достаточные условия, при выполнении которых плотность множеств представимых чисел положительна для всех классов вычетов по данному модулю k. Обобщается известная теорема Н.П. Романова на случай, когда представимые числа принадлежат арифметической прогрессии.
In the work the following problem is considered about distribution of the natural numbers belonging to the set class of deductions on some module and representable in the form of the sum u+v, where u, v are the members of two set sequences of natural numbers. Sufficient conditions are received at performance of which the density of sets of representable numbers is positive for all classes of deductions on the given module k. N.P. Romanov's known theorem for n a case when representable numbers belong to an arithmetic progression is generalised.
Мы рассмотрим здесь вопрос
о распределении натуральных чисел, принадлежащих заданному классу
вычетов по некоторому модулю и представимых в виде суммы
где
и
члены двух заданных последовательностей натуральных чисел. При этом
мы исследуем вопрос о зависимости числа представимых чисел интервала
при условии, когда модуль растет вместе с длиной интервала.
Рассмотрим сначала задачу
Н.П.Романова [1] о числах представимых в форме
где
- пробегает простые числа,
- натуральные числа,
- заданное целое число
обобщив ее на случай, когда представимые числа принадлежат
арифметической прогрессии.
Пусть
- число представлений натурального числа
суммой
и
- заданные целые числа, причем
Согласно тождеству Романова
где
В
дальнейшем целое число
не будет меняться в течение наших рассуждений.
Введем в рассмотрение функцию
означающую
показатель числа
по модулю
,
т.е. наименьшее среди натуральных чисел, таких что
(отсюда видно, что функция
определена для тех
которые взаимно просты с а).
Отметим,
что
однако функция
не является мультипликативной. Например, если
и
- различные простые числа, и число
является первообразным корнем по модулям
и
одновременно, то
из мультипликативности функции
следовало бы, что
,
в то время первообразных корней по модулю
как известно не существует.
Лемма
1.
Если
то
Действительно, т.к.
и
то
Из известных свойств показателя вытекает, что
Лемма
2.
Пусть
Тогда справедливо равенство
Д о к а з а т е л ь с т в о. Пользуясь известным свойством функции Мебиуса, получаем:
Если
и
- наименьшее из тех натуральных для которых
то сравнение
равносильно сравнению
Так как
то
и последнее сравнение означает, что
т.е.
По лемме 1
множество чисел
разбивается на
полных систем вычетов по
в каждой из которых содержится ровно одно число
удовлетворяющее сравнению
Поэтому
откуда следует утверждение леммы.
Мы можем
теперь оценить снизу величину
Если
то по теореме Зигеля-Вальфиша при
(где
- любое фиксированное положительное число&#﴿;
справедливо
неравенство
где
- абсолютная
положительная константа. Поэтому
В силу леммы 2 последняя сумма равна
Положим
Из леммы 2
следует, что
и
Оценим
сверху величину
Применим метод решета к задаче об оценке величины
где
и
- натуральные числа,
и
- целые числа,
и
- простые числа.
Простые
числа
сравнимое с
по модулю
такие что
- простое число сравнимое с
(отсюда следует, что
)
принадлежат множеству целых чисел, остающихся после вычеркивания из
нулевых классов вычетов и классов вычетов, определяемых числом
по простым модулям, а также всех классов вычетов кроме определяемого
числом
по простым делителем
Так как
причем
то речь идет о натуральных числах
таких, что числа
и
- одновременно простые. Воспользуемся следующей леммой.
Лемма
3.
Пусть
- целые числа,
Тогда число натуральных чисел
не превосходящих
таких, что числа
- одновременно простые не превосходят
,
где
- число решений сравнения
Д о
к а з а т е л ь с т в о.
Имеется
в [4].
Применим лемму 3 к случаю
Тогда
- число решений сравнения
Поэтому
при
если
и
При
имеем:
Отсюда следует:
Оценим
последнюю сумму как функцию от
Положим
Так как
то
Внутренняя сумма равна
Поэтому
Пусть
- любое натуральное число, тогда
Так как
и
то ввиду очевидной оценки
имеем:
Отсюда преобразованием Абеля получаем:
Объединяя полученные оценки, имеем:
Откуда
Воспользуемся теперь неравенством Романова–Шнирельмана [4], согласно которому
(в данном
случае
- количество чисел прогрессии
непревосходящих
,
представимых в форме
).
Так как
правая часть неравенства возрастает по
и убывает по
,
то из полученных оценок
и
следует:
при
условии
(заметим,
что так как
последнее условие обеспечивает оценку
&#﴿;</FONT></SPAN>.</P>
<P>Таким
образом справедлива</P>
<P><I><B>Теорема
1.</B></I>
Пусть
<A HREF="images/m1cb1b88b.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/m1cb1b88b.gif" NAME="Объект155" ALIGN=ABSMIDDLE WIDTH=84 HEIGHT=21></A>
- число натуральных чисел
<A HREF="images/71be596.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/71be596.gif" NAME="Объект156" ALIGN=ABSMIDDLE WIDTH=92 HEIGHT=18></A>
представимых в форме<A HREF="images/m131bc90e.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/m131bc90e.gif" NAME="Объект157" ALIGN=ABSMIDDLE WIDTH=51 HEIGHT=20></A>и
не превосходящих
<A HREF="images/m6c768d16.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/m6c768d16.gif" NAME="Объект158" ALIGN=ABSMIDDLE WIDTH=18 HEIGHT=18></A>,
</P>
<P><A HREF="images/m2b64f50.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/m2b64f50.gif" NAME="Объект159" ALIGN=ABSMIDDLE WIDTH=164 HEIGHT=45></A></P>
<P>где
<A HREF="images/m47548578.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/m47548578.gif" NAME="Объект160" ALIGN=ABSMIDDLE WIDTH=95 HEIGHT=21></A>
- показатель числа
<A HREF="images/3b82c5d0.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/3b82c5d0.gif" NAME="Объект161" ALIGN=ABSMIDDLE WIDTH=18 HEIGHT=18></A>
по модулю
<A HREF="images/19cd8087.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/19cd8087.gif" NAME="Объект162" ALIGN=ABSMIDDLE WIDTH=20 HEIGHT=18></A>,
</P>
<P><A HREF="images/6818b31c.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/6818b31c.gif" NAME="Объект163" ALIGN=ABSMIDDLE WIDTH=161 HEIGHT=42></A></P>
<P>Тогда,
если
<A HREF="images/2bd1446e.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/2bd1446e.gif" NAME="Объект164" ALIGN=ABSMIDDLE WIDTH=162 HEIGHT=18></A>
то имеет место неравенство</P>
<P><A HREF="images/5461e10f.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/5461e10f.gif" NAME="Объект165" ALIGN=ABSMIDDLE WIDTH=332 HEIGHT=46></A></P>
<P>где
<A HREF="images/m441a9fef.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/m441a9fef.gif" NAME="Объект166" ALIGN=ABSMIDDLE WIDTH=17 HEIGHT=18></A>
- положительная абсолютная константа.
</P>
<P>Заметим,
что условие
<A HREF="images/386e4c27.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/386e4c27.gif" NAME="Объект167" ALIGN=ABSMIDDLE WIDTH=82 HEIGHT=18></A>
существенно: при нарушении его множество чисел прогрессии
<A HREF="images/2f7fec9.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/2f7fec9.gif" NAME="Объект168" ALIGN=ABSMIDDLE WIDTH=55 HEIGHT=18></A>
представимых в форме
<A HREF="images/m131bc90e.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/m131bc90e.gif" NAME="Объект169" ALIGN=ABSMIDDLE WIDTH=51 HEIGHT=20></A>,
имеет нулевую асимптотическую плотность.</P>
<P>Действительно
<A HREF="images/m46e72a54.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/m46e72a54.gif" NAME="Объект170" ALIGN=ABSMIDDLE WIDTH=202 HEIGHT=21></A></P>
<P><A HREF="images/6ed340f5.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/6ed340f5.gif" NAME="Объект171" ALIGN=ABSMIDDLE WIDTH=102 HEIGHT=74></A></P>
<P><A HREF="images/m4eeebfe.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/m4eeebfe.gif" NAME="Объект172" ALIGN=ABSMIDDLE WIDTH=133 HEIGHT=72></A></P>
<P><A HREF="images/3d7fff9e.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/3d7fff9e.gif" NAME="Объект173" ALIGN=ABSMIDDLE WIDTH=209 HEIGHT=82></A></P>
<P>Так как</P>
<P><A HREF="images/m1327ec01.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/m1327ec01.gif" NAME="Объект174" ALIGN=ABSMIDDLE WIDTH=231 HEIGHT=76></A></P>
<P>то отсюда
следует:</P>
<P><A HREF="images/2cb0bf61.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/2cb0bf61.gif" NAME="Объект175" ALIGN=ABSMIDDLE WIDTH=131 HEIGHT=72></A></P>
<P>Как было
установлено выше,</P>
<P><A HREF="images/m591e5778.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/m591e5778.gif" NAME="Объект176" ALIGN=ABSMIDDLE WIDTH=230 HEIGHT=59></A></P>
<P>Отсюда и
из предыдущей оценки вытекает, что</P>
<P><A HREF="images/m277a8b6a.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/m277a8b6a.gif" NAME="Объект177" ALIGN=ABSMIDDLE WIDTH=272 HEIGHT=22></A></P>
<P>В связи с
этим представляет интерес исследование вопроса о положительности
суммы</P>
<P><A HREF="images/35ffdaa9.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/35ffdaa9.gif" NAME="Объект178" ALIGN=ABSMIDDLE WIDTH=189 HEIGHT=47></A></P>
<P>Так как
при
<A HREF="images/m5f9727a1.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/m5f9727a1.gif" NAME="Объект179" ALIGN=ABSMIDDLE WIDTH=88 HEIGHT=18></A>
числа
<A HREF="images/e338565.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/e338565.gif" NAME="Объект180" ALIGN=ABSMIDDLE WIDTH=46 HEIGHT=20></A>
попарно несравнимы по модулю
<A HREF="images/70ca4404.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/70ca4404.gif" NAME="Объект181" ALIGN=ABSMIDDLE WIDTH=19 HEIGHT=18></A>,
а число непримитивных классов вычетов по модулю
<A HREF="images/70ca4404.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/70ca4404.gif" NAME="Объект182" ALIGN=ABSMIDDLE WIDTH=19 HEIGHT=18></A>
есть
<A HREF="images/20061537.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/20061537.gif" NAME="Объект183" ALIGN=ABSMIDDLE WIDTH=70 HEIGHT=18></A>
то при условии
<A HREF="images/49f56792.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/49f56792.gif" NAME="Объект184" ALIGN=ABSMIDDLE WIDTH=109 HEIGHT=18></A>
по крайней мере одно из чисел
<A HREF="images/e338565.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/e338565.gif" NAME="Объект185" ALIGN=ABSMIDDLE WIDTH=46 HEIGHT=20></A>
попадает в примитивный класс и
<A HREF="images/m2de8bcf2.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/m2de8bcf2.gif" NAME="Объект186" ALIGN=ABSMIDDLE WIDTH=105 HEIGHT=21></A>
Следовательно справедливо
</P>
<P><I><U><B>Теорема</B></U></I><SPAN LANG="tk-TM"><I><U><B>
</B></U></I></SPAN><I><U><B>2.</B></U></I><B>
</B>Пусть
<A HREF="images/m72d587c2.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/m72d587c2.gif" NAME="Объект187" ALIGN=ABSMIDDLE WIDTH=50 HEIGHT=18></A>
- целые числа,
<A HREF="images/m71037755.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/m71037755.gif" NAME="Объект188" ALIGN=ABSMIDDLE WIDTH=95 HEIGHT=18></A>
<A HREF="images/m7a47a674.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/m7a47a674.gif" NAME="Объект189" ALIGN=ABSMIDDLE WIDTH=166 HEIGHT=21></A>
- показатель числа
<A HREF="images/3b82c5d0.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/3b82c5d0.gif" NAME="Объект190" ALIGN=ABSMIDDLE WIDTH=18 HEIGHT=18></A>
по
<A HREF="images/me8620c2.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/me8620c2.gif" NAME="Объект191" ALIGN=ABSMIDDLE WIDTH=56 HEIGHT=18></A>
Если
<A HREF="images/49f56792.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/49f56792.gif" NAME="Объект192" ALIGN=ABSMIDDLE WIDTH=109 HEIGHT=18></A>,
то число чисел любого класса вычетов по
<A HREF="images/3e1998eb.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/3e1998eb.gif" NAME="Объект193" ALIGN=ABSMIDDLE WIDTH=50 HEIGHT=18></A>,
представимых в виде
<A HREF="images/m131bc90e.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/m131bc90e.gif" NAME="Объект194" ALIGN=ABSMIDDLE WIDTH=51 HEIGHT=20></A>
имеет положительную асимптотическую плотность. Это обобщение
известной теоремы Н.П.Романова, которая следует отсюда при
<A HREF="images/m4b7d181b.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/m4b7d181b.gif" NAME="Объект195" ALIGN=ABSMIDDLE WIDTH=45 HEIGHT=18></A></P>
<P>В
частности, если
<A HREF="images/70ca4404.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/70ca4404.gif" NAME="Объект196" ALIGN=ABSMIDDLE WIDTH=19 HEIGHT=18></A>
- простое число, то
<A HREF="images/6959be75.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/6959be75.gif" NAME="Объект197" ALIGN=ABSMIDDLE WIDTH=85 HEIGHT=18></A>
и поскольку
<A HREF="images/m4b70f1d6.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/m4b70f1d6.gif" NAME="Объект198" ALIGN=ABSMIDDLE WIDTH=157 HEIGHT=38></A>
при
<A HREF="images/m4e702e12.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/m4e702e12.gif" NAME="Объект199" ALIGN=ABSMIDDLE WIDTH=48 HEIGHT=18></A>
получаем такое
</P>
<P><I><U><B>Следствие
1.</B></U></I>
Если
<A HREF="images/m14202b41.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/m14202b41.gif" NAME="Объект200" ALIGN=ABSMIDDLE WIDTH=40 HEIGHT=18></A>
- целое число, то в каждом классе вычетов по простому модулю
<A HREF="images/m55b22fa1.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/m55b22fa1.gif" NAME="Объект201" ALIGN=ABSMIDDLE WIDTH=41 HEIGHT=18></A>
число чисел представимых в форме
<A HREF="images/m131bc90e.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/m131bc90e.gif" NAME="Объект202" ALIGN=ABSMIDDLE WIDTH=51 HEIGHT=20></A>
имеет положительную асимптотическую плотность.</P>
<P>Рассмотрим
другой частный случай, когда число
<A HREF="images/3b82c5d0.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/3b82c5d0.gif" NAME="Объект203" ALIGN=ABSMIDDLE WIDTH=18 HEIGHT=18></A>
является первообразным корнем по
<A HREF="images/m4756ca21.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/m4756ca21.gif" NAME="Объект204" ALIGN=ABSMIDDLE WIDTH=50 HEIGHT=18></A>,
т.е.
<A HREF="images/6b3bcf71.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/6b3bcf71.gif" NAME="Объект205" ALIGN=ABSMIDDLE WIDTH=98 HEIGHT=21></A></P>
<P>В этом
случае, наше условие означает, что
<A HREF="images/m3c88b9cd.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/m3c88b9cd.gif" NAME="Объект206" ALIGN=ABSMIDDLE WIDTH=82 HEIGHT=57></A>
Если
<A HREF="images/71882d00.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/71882d00.gif" NAME="Объект207" ALIGN=ABSMIDDLE WIDTH=47 HEIGHT=20></A>,
где
<A HREF="images/m55ed7f30.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/m55ed7f30.gif" NAME="Объект208" ALIGN=ABSMIDDLE WIDTH=40 HEIGHT=18></A>
- простое число, то
<A HREF="images/m5cd0d70d.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/m5cd0d70d.gif" NAME="Объект209" ALIGN=ABSMIDDLE WIDTH=160 HEIGHT=38></A>
Поэтому из теоремы 2. вытекает также</P>
<P><I><U><B>Следствие
2</B></U></I><U><B>.
</B></U>
Если
<A HREF="images/m39cde112.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/m39cde112.gif" NAME="Объект210" ALIGN=ABSMIDDLE WIDTH=18 HEIGHT=18></A>
- нечетное простое число,
<A HREF="images/m6f100910.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/m6f100910.gif" NAME="Объект211" ALIGN=ABSMIDDLE WIDTH=18 HEIGHT=18></A>
и
<A HREF="images/3b82c5d0.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/3b82c5d0.gif" NAME="Объект212" ALIGN=ABSMIDDLE WIDTH=18 HEIGHT=18></A>
- целые числа,
<A HREF="images/m7bdf3a6a.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/m7bdf3a6a.gif" NAME="Объект213" ALIGN=ABSMIDDLE WIDTH=44 HEIGHT=18></A>
причем
<A HREF="images/3b82c5d0.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/3b82c5d0.gif" NAME="Объект214" ALIGN=ABSMIDDLE WIDTH=18 HEIGHT=18></A>
- есть первообразный корень по
<A HREF="images/m45f91701.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/m45f91701.gif" NAME="Объект215" ALIGN=ABSMIDDLE WIDTH=56 HEIGHT=20></A>,
то множество чисел любого класса вычетов по
<A HREF="images/6c0f50a9.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/6c0f50a9.gif" NAME="Объект216" ALIGN=ABSMIDDLE WIDTH=56 HEIGHT=20></A>,
представимых в форме
<A HREF="images/m131bc90e.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/m131bc90e.gif" NAME="Объект217" ALIGN=ABSMIDDLE WIDTH=51 HEIGHT=20></A>
имеет положительную асимптотическую плотность.</P>
<P>Литература:</P>
<OL>
<LI VALUE=1><P><SPAN LANG="tk-TM">Romano</SPAN><SPAN LANG="en-US">v</SPAN><SPAN LANG="tk-TM">
N.P. Uber einige Sartze der additi</SPAN><SPAN LANG="en-US">v</SPAN><SPAN LANG="tk-TM">en
Zahlentheorie, Math. Ann.109 (1934).668-678.</SPAN><LI><P>
<SPAN LANG="tk-TM">Selberg
S. A </SPAN><SPAN LANG="tk-TM">generalization
of a theorem of Romanoff, Kong. Norse </SPAN><SPAN LANG="en-US">vid.Selsc.For
handl.35,17 (1962),91-95</SPAN><LI><P>
Ф<SPAN LANG="tk-TM">a</SPAN>йнлейб
А.С., Оразов М. Бинарные аддитивные задачи с показательной функцией.
Литовский математический сборник. 1978. №4.с.187-198.<LI><P>
Оразов М. Аддитивные
задачи с редкими последовательностями, канд. диссертация,
Чарджоу,1982.</OL>
