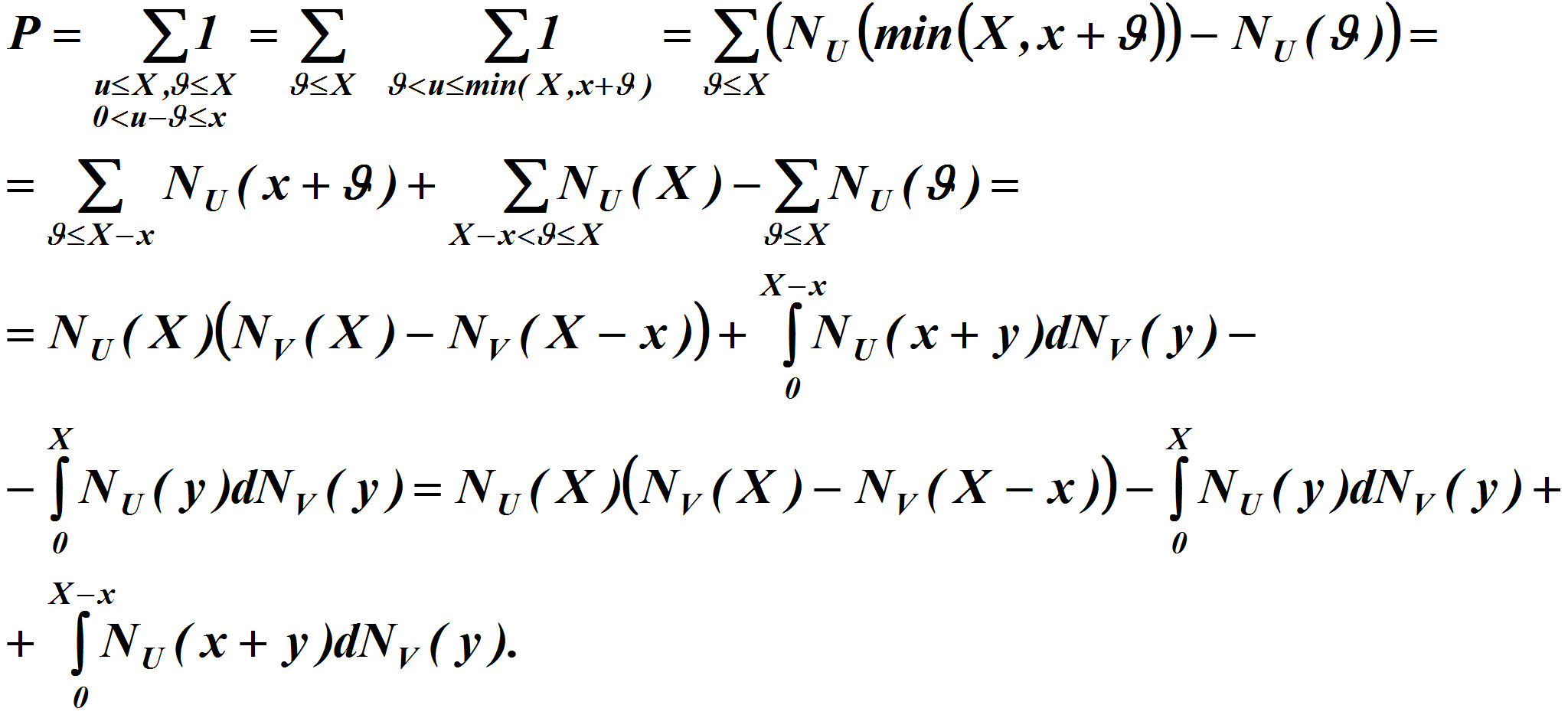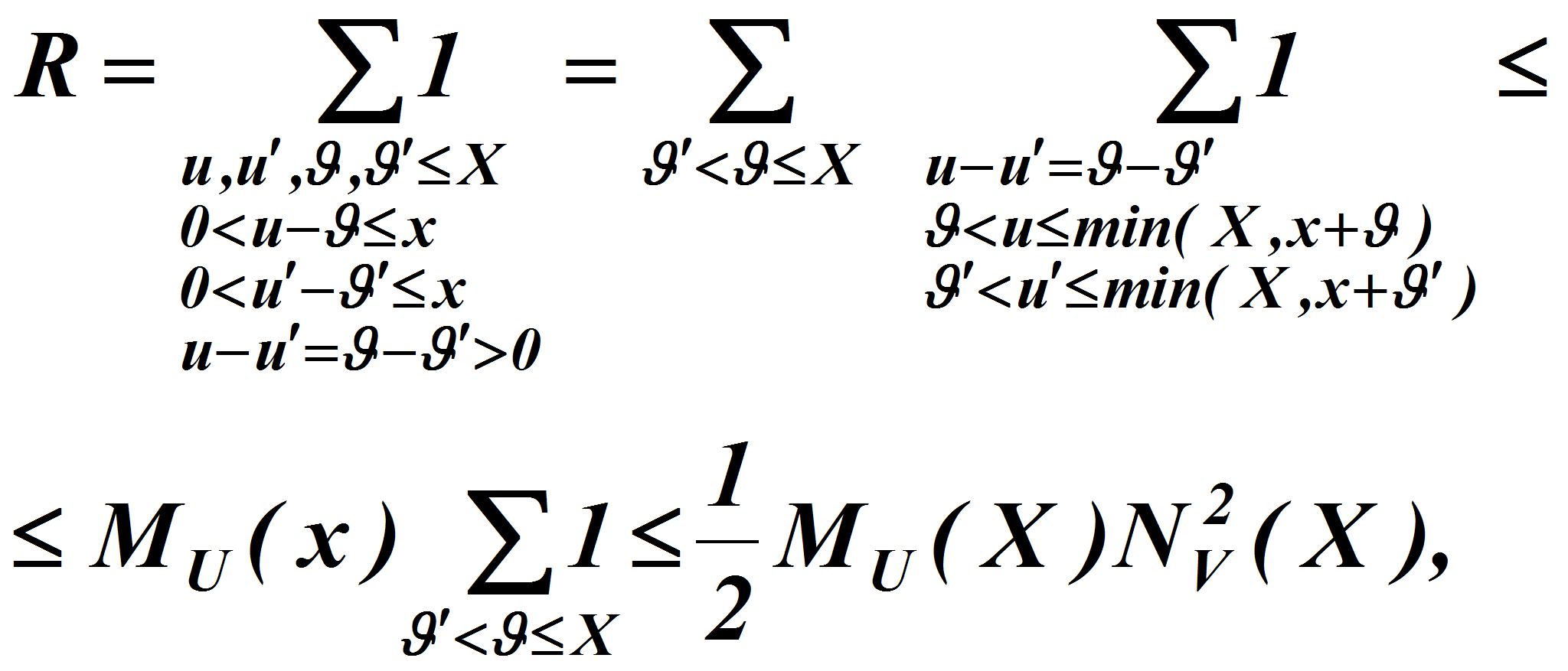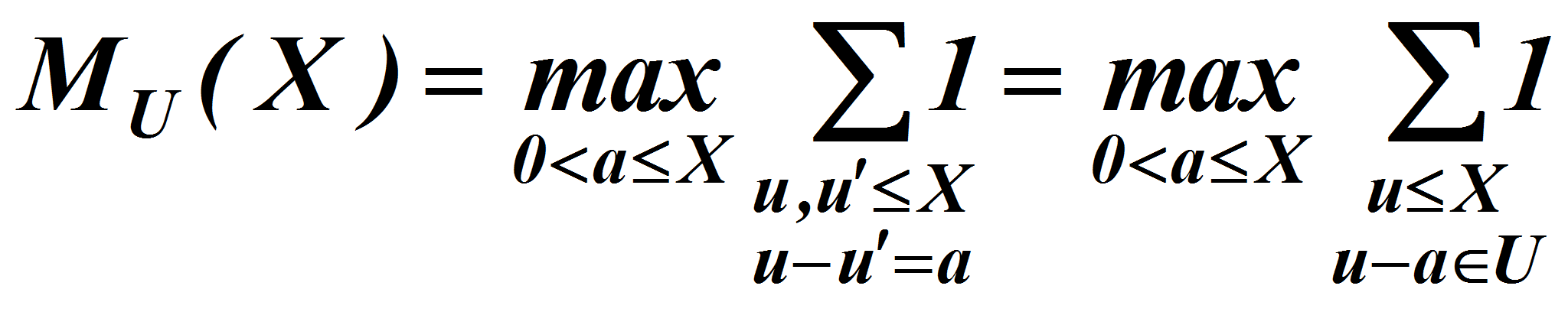The present work
researches the density of sequence of natural numbers, belonging
within a specified interval and presentable as a difference between
members of two specified sequences of natural numbers U
and V.
Using the identical equation of N. P. Romanoff and the Romanoff-Erdцs
inequality asymptotic formulae, characterising the quantity of
natural numbers presentable as a difference of ak
– bl,
where a and
b
– natural numbers, k
≥ 2, l ≥ 2 – whole
numbers, have been obtained. Asymptotic formulae for the quantity of
natural numbers, not exceeding a specified limit and presentable as a
difference u
- ∂, (u
U and ∂
V) in one
way only, have been obtained.
В данной работе изучается плотность
последовательности натуральных чисел, принадлежащих заданному
интервалу и представимых в виде разности членов двух заданных
последовательностей натуральных чисел
и
.
С помощью тождества Н.П.Романова и
неравенства Романова−Эрдоша получены асимптотические формулы,
характеризующие количество натуральных чисел, представимых в виде
разности
,
где
и
− натуральные числа,
,
−
целые числа. Получены также асимптотические формулы для числа
натуральных чисел, непревосходящих заданной границы и представимых в
виде разности
,
(
и
)
единственным образом.
Пусть
и
две последовательности натуральных чисел. Мы рассматриваем
натуральные числа
представимые в виде
,
где
,
(в
дальнейшем включения
и
подразумевается
если явно не оговорено противное).
Применим тождество Романова к множеству
,
образованному парами (
),
где
,
,
и
.
Обозначим через
и
соответственно
подсчитывающие функции последовательностей
а через
&#;
число пар из
.
В этих обозначениях
Обозначим через
число представлений натурального
в виде разности
,
где
,
.
Согласно тождеству Романова [1]
,
где
где
.
Пусть
&#;</FONT>
число натуральных чисел
<A HREF="images/m60791d63.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/m60791d63.gif" NAME="Объект40" ALIGN=ABSMIDDLE WIDTH=40 HEIGHT=18></A>,
представимых в виде разности
<A HREF="images/3d8fc92c.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/3d8fc92c.gif" NAME="Объект41" ALIGN=ABSMIDDLE WIDTH=41 HEIGHT=18></A>,
где
<A HREF="images/m1f9be600.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/m1f9be600.gif" NAME="Объект42" ALIGN=ABSMIDDLE WIDTH=63 HEIGHT=18></A>,
а
<A HREF="images/m21f7063f.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/m21f7063f.gif" NAME="Объект43" ALIGN=ABSMIDDLE WIDTH=196 HEIGHT=21></A><FONT FACE="Symbol">&#;</FONT>
число натуральных чисел
<A HREF="images/m60791d63.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/m60791d63.gif" NAME="Объект44" ALIGN=ABSMIDDLE WIDTH=40 HEIGHT=18></A>,
представимых в указанном виде единственным образом. В силу
неравенства Романова<FONT FACE="Symbol">&#;</FONT>Эрдоша
[1]<P>
<A HREF="images/m3f7dbd33.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/m3f7dbd33.gif" NAME="Объект45" ALIGN=ABSMIDDLE WIDTH=365 HEIGHT=118></A><P>
С другой стороны<P>
<A HREF="images/56c6fa8c.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/56c6fa8c.gif" NAME="Объект46" ALIGN=ABSMIDDLE WIDTH=168 HEIGHT=34></A><P>
Так как<P>
<A HREF="images/bd89b8.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/bd89b8.gif" NAME="Объект47" ALIGN=ABSMIDDLE WIDTH=389 HEIGHT=141></A><P>
то<P>
<A HREF="images/m2075087e.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/m2075087e.gif" NAME="Объект48" ALIGN=ABSMIDDLE WIDTH=464 HEIGHT=48></A><P>
Таким образом справедлива<P>
<I><B>Теорема 1</B></I>. Имеют место
соотношения<P>
<A HREF="images/m34aecca2.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/m34aecca2.gif" NAME="Объект49" ALIGN=ABSMIDDLE WIDTH=382 HEIGHT=72></A><P>
<A HREF="images/68e37c4e.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/68e37c4e.gif" NAME="Объект50" ALIGN=ABSMIDDLE WIDTH=387 HEIGHT=72></A><P>
где
<A HREF="images/5fbe1c4f.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/5fbe1c4f.gif" NAME="Объект51" ALIGN=ABSMIDDLE WIDTH=89 HEIGHT=21></A>.<P>
Пусть
<A HREF="images/me3c3a34.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/me3c3a34.gif" NAME="Объект52" ALIGN=ABSMIDDLE WIDTH=52 HEIGHT=18></A>
означает число натуральных чисел, представимых в виде разности
<A HREF="images/3d8fc92c.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/3d8fc92c.gif" NAME="Объект53" ALIGN=ABSMIDDLE WIDTH=41 HEIGHT=18></A>,
где
<A HREF="images/m1f9be600.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/m1f9be600.gif" NAME="Объект54" ALIGN=ABSMIDDLE WIDTH=63 HEIGHT=18></A>,
а
<A HREF="images/m3df7f4e5.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/m3df7f4e5.gif" NAME="Объект55" ALIGN=ABSMIDDLE WIDTH=57 HEIGHT=21></A><FONT FACE="Symbol">&#;</FONT>
число натуральных чисел, представимых в указанном виде единственным
образом. Очевидно,
<A HREF="images/m2551c170.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/m2551c170.gif" NAME="Объект56" ALIGN=ABSMIDDLE WIDTH=137 HEIGHT=18></A>
<A HREF="images/m19bfc22e.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/m19bfc22e.gif" NAME="Объект57" ALIGN=ABSMIDDLE WIDTH=142 HEIGHT=21></A>.
Поэтому при
<A HREF="images/4a4d357e.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/4a4d357e.gif" NAME="Объект58" ALIGN=ABSMIDDLE WIDTH=46 HEIGHT=18></A>
из теоремы 1 следует<P>
<I><B>Теорема 2.</B></I> В условиях
теоремы 1<P>
<A HREF="images/585106bd.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/585106bd.gif" NAME="Объект59" ALIGN=ABSMIDDLE WIDTH=304 HEIGHT=48></A><P>
и<P>
<A HREF="images/6045049c.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/6045049c.gif" NAME="Объект60" ALIGN=ABSMIDDLE WIDTH=319 HEIGHT=48></A>,
<A HREF="images/5fbe1c4f.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/5fbe1c4f.gif" NAME="Объект61" ALIGN=ABSMIDDLE WIDTH=89 HEIGHT=21></A>.<P>
Ясно, что последний интеграл
<A HREF="images/mc86999e.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/mc86999e.gif" NAME="Объект62" ALIGN=ABSMIDDLE WIDTH=112 HEIGHT=21></A>.
С другой стороны, если
<A HREF="images/3fe56eaf.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/3fe56eaf.gif" NAME="Объект63" ALIGN=ABSMIDDLE WIDTH=70 HEIGHT=18></A>,
то<P>
<A HREF="images/m56b6f214.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/m56b6f214.gif" NAME="Объект64" ALIGN=ABSMIDDLE WIDTH=450 HEIGHT=48></A><P>
Если существует функция
<A HREF="images/5d547e2b.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/5d547e2b.gif" NAME="Объект65" ALIGN=ABSMIDDLE WIDTH=103 HEIGHT=18></A>
при
<A HREF="images/m54915701.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/m54915701.gif" NAME="Объект66" ALIGN=ABSMIDDLE WIDTH=53 HEIGHT=18></A>,
такая, что<P>
<A HREF="images/m303d79d6.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/m303d79d6.gif" NAME="Объект67" ALIGN=ABSMIDDLE WIDTH=137 HEIGHT=23></A>
и
<A HREF="images/m56879b9e.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/m56879b9e.gif" NAME="Объект68" ALIGN=ABSMIDDLE WIDTH=121 HEIGHT=21></A>,<P>
то при
<A HREF="images/m5165fd26.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/m5165fd26.gif" NAME="Объект69" ALIGN=ABSMIDDLE WIDTH=74 HEIGHT=18></A>
имеем<P>
<A HREF="images/6741f234.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/6741f234.gif" NAME="Объект70" ALIGN=ABSMIDDLE WIDTH=301 HEIGHT=23></A><P>
и следовательно<P>
<A HREF="images/m1d695ade.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/m1d695ade.gif" NAME="Объект71" ALIGN=ABSMIDDLE WIDTH=251 HEIGHT=48></A><P>
Если при этом
<A HREF="images/67ef63a6.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/67ef63a6.gif" NAME="Объект72" ALIGN=ABSMIDDLE WIDTH=149 HEIGHT=23></A>
и
<A HREF="images/m7f2350a2.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/m7f2350a2.gif" NAME="Объект73" ALIGN=ABSMIDDLE WIDTH=155 HEIGHT=49></A>,<P>
то<P>
<A HREF="images/4043ce71.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/4043ce71.gif" NAME="Объект74" ALIGN=ABSMIDDLE WIDTH=255 HEIGHT=25></A>.<P>
Таким образом, имеет место<P>
<I><B>Теорема 3</B></I>. Пусть
<A HREF="images/m4c138a78.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/m4c138a78.gif" NAME="Объект75" ALIGN=ABSMIDDLE WIDTH=23 HEIGHT=18></A>
и
<A HREF="images/2c16c634.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/2c16c634.gif" NAME="Объект76" ALIGN=ABSMIDDLE WIDTH=22 HEIGHT=18></A>
<FONT FACE="Symbol">&#;</FONT>
последовательности натуральных чисел такие, что<P>
<A HREF="images/25e3212b.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/25e3212b.gif" NAME="Объект77" ALIGN=ABSMIDDLE WIDTH=156 HEIGHT=23></A>
<A HREF="images/m7f2350a2.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/m7f2350a2.gif" NAME="Объект78" ALIGN=ABSMIDDLE WIDTH=155 HEIGHT=49></A><P>
и существует функция
<A HREF="images/5d547e2b.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/5d547e2b.gif" NAME="Объект79" ALIGN=ABSMIDDLE WIDTH=103 HEIGHT=18></A>
(при
<A HREF="images/m54915701.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/m54915701.gif" NAME="Объект80" ALIGN=ABSMIDDLE WIDTH=53 HEIGHT=18></A>),
такая, что
<P>
<A HREF="images/m453f4970.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/m453f4970.gif" NAME="Объект81" ALIGN=ABSMIDDLE WIDTH=144 HEIGHT=23></A>
и
<A HREF="images/m56879b9e.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/m56879b9e.gif" NAME="Объект82" ALIGN=ABSMIDDLE WIDTH=121 HEIGHT=21></A>.<P>
Тогда при
<A HREF="images/m54915701.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/m54915701.gif" NAME="Объект83" ALIGN=ABSMIDDLE WIDTH=53 HEIGHT=18></A><P>
<A HREF="images/7b031324.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/7b031324.gif" NAME="Объект84" ALIGN=ABSMIDDLE WIDTH=170 HEIGHT=21></A><P>
и<P>
<A HREF="images/dfdd6af.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/dfdd6af.gif" NAME="Объект85" ALIGN=ABSMIDDLE WIDTH=175 HEIGHT=21></A>.<P>
<I><B>Замечание</B></I>. Как видно
из определения величины
<A HREF="images/5f60cf10.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/5f60cf10.gif" NAME="Объект86" ALIGN=ABSMIDDLE WIDTH=21 HEIGHT=18></A>,<P>
<SUP>
<A HREF="images/m1041773b.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/m1041773b.gif" NAME="Объект87" ALIGN=BOTTOM WIDTH=81 HEIGHT=69></A></SUP>.<P>
Последняя сумма симметрична относительно
<A HREF="images/m4c138a78.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/m4c138a78.gif" NAME="Объект88" ALIGN=ABSMIDDLE WIDTH=23 HEIGHT=18></A>
и
<A HREF="images/2c16c634.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/2c16c634.gif" NAME="Объект89" ALIGN=ABSMIDDLE WIDTH=22 HEIGHT=18></A>.
Поэтому наряду с оценкой<P>
<A HREF="images/2d6811e0.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/2d6811e0.gif" NAME="Объект90" ALIGN=ABSMIDDLE WIDTH=155 HEIGHT=38></A>,<P>
полученной выше, справедливо также неравенство<P>
<A HREF="images/m18dd27.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/m18dd27.gif" NAME="Объект91" ALIGN=ABSMIDDLE WIDTH=155 HEIGHT=38></A>.<P>
Отсюда следует, что утверждение теоремы 2 остается
справедливым, если в вычитаемых членах заменить
<A HREF="images/5fff6862.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/5fff6862.gif" NAME="Объект92" ALIGN=ABSMIDDLE WIDTH=117 HEIGHT=24></A>
на
<A HREF="images/m391d548c.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/m391d548c.gif" NAME="Объект93" ALIGN=ABSMIDDLE WIDTH=117 HEIGHT=24></A>.<P>
Ввиду асимметрии исходной задачи относительно
<A HREF="images/m4c138a78.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/m4c138a78.gif" NAME="Объект94" ALIGN=ABSMIDDLE WIDTH=23 HEIGHT=18></A>
и
<A HREF="images/2c16c634.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/2c16c634.gif" NAME="Объект95" ALIGN=ABSMIDDLE WIDTH=22 HEIGHT=18></A>,
такая замена позволяет в ряде случаев получать новые результаты.<P>
Применим теорему 2 к последовательностям степеней
<A HREF="images/5043eb8f.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/5043eb8f.gif" NAME="Объект96" ALIGN=ABSMIDDLE WIDTH=65 HEIGHT=22></A>,
<A HREF="images/m5241f5de.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/m5241f5de.gif" NAME="Объект97" ALIGN=ABSMIDDLE WIDTH=61 HEIGHT=22></A>,
где
<A HREF="images/496b3a1e.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/496b3a1e.gif" NAME="Объект98" ALIGN=ABSMIDDLE WIDTH=19 HEIGHT=18></A>
и
<A HREF="images/2f7bd377.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/2f7bd377.gif" NAME="Объект99" ALIGN=ABSMIDDLE WIDTH=15 HEIGHT=18></A>заданные
целые числа <FONT FACE="Symbol">&#;</FONT>2.<P>
Тогда<P>
<A HREF="images/m2442ec25.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/m2442ec25.gif" NAME="Объект100" ALIGN=ABSMIDDLE WIDTH=193 HEIGHT=39></A>,<P>
<A HREF="images/m7653c3ba.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/m7653c3ba.gif" NAME="Объект101" ALIGN=ABSMIDDLE WIDTH=191 HEIGHT=39></A>.<P>
Как было доказано в работе [1], в этом случае
<A HREF="images/419ccca9.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/419ccca9.gif" NAME="Объект102" ALIGN=ABSMIDDLE WIDTH=123 HEIGHT=24></A>,
<A HREF="images/43ea2ced.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/43ea2ced.gif" NAME="Объект103" ALIGN=ABSMIDDLE WIDTH=122 HEIGHT=24></A>,
для любого фиксированного
<A HREF="images/m358502df.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/m358502df.gif" NAME="Объект104" ALIGN=ABSMIDDLE WIDTH=39 HEIGHT=18></A>.<P>
По теореме 2<P>
<A HREF="images/724ce6d0.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/724ce6d0.gif" NAME="Объект105" ALIGN=ABSMIDDLE WIDTH=245 HEIGHT=269></A><P>
Если
<A HREF="images/75bf8e65.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/75bf8e65.gif" NAME="Объект106" ALIGN=ABSMIDDLE WIDTH=71 HEIGHT=38></A>,
то есть
<A HREF="images/3976db94.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/3976db94.gif" NAME="Объект107" ALIGN=ABSMIDDLE WIDTH=38 HEIGHT=18></A>,
то главный член не поглощается остатком, ввиду<SPAN LANG="sq-AL">
</SPAN>произвольной малости
<A HREF="images/38326d0f.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/38326d0f.gif" NAME="Объект108" ALIGN=ABSMIDDLE WIDTH=44 HEIGHT=18></A><P>
В силу предыдущих замечаний второй остаточный член можно
заменить на
<A HREF="images/m1022ca5c.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/m1022ca5c.gif" NAME="Объект109" ALIGN=ABSMIDDLE WIDTH=72 HEIGHT=37></A>.
Это соответствует оценке
<A HREF="images/m391d548c.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/m391d548c.gif" NAME="Объект110" ALIGN=ABSMIDDLE WIDTH=117 HEIGHT=24></A>.
<P>Согласно теореме 2, точно также
получается и оценка
<A HREF="images/m3df7f4e5.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/m3df7f4e5.gif" NAME="Объект111" ALIGN=ABSMIDDLE WIDTH=57 HEIGHT=21></A>.
Поэтому справедлива следующая<P>
<I><B>Теорема 4.</B></I> Пусть
<A HREF="images/496b3a1e.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/496b3a1e.gif" NAME="Объект112" ALIGN=ABSMIDDLE WIDTH=19 HEIGHT=18></A>
и
<A HREF="images/2f7bd377.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/2f7bd377.gif" NAME="Объект113" ALIGN=ABSMIDDLE WIDTH=15 HEIGHT=18></A>
неравные друг другу целые числа <FONT FACE="Symbol">&#;</FONT>2.
Тогда число натуральных чисел, непревосходящих
<A HREF="images/m36a401fc.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/m36a401fc.gif" NAME="Объект114" ALIGN=ABSMIDDLE WIDTH=24 HEIGHT=18></A>
и представимых в виде разности
<A HREF="images/48196b71.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/48196b71.gif" NAME="Объект115" ALIGN=ABSMIDDLE WIDTH=50 HEIGHT=20></A>,
в котором уменьшаемое и вычитаемое также не превосходит
<A HREF="images/m36a401fc.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/m36a401fc.gif" NAME="Объект116" ALIGN=ABSMIDDLE WIDTH=24 HEIGHT=18></A>,
а также число натуральных чисел, непревосходящих
<A HREF="images/m36a401fc.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/m36a401fc.gif" NAME="Объект117" ALIGN=ABSMIDDLE WIDTH=24 HEIGHT=18></A>
и представимых в указанном виде единственным образом асимптотически
равно<P>
<A HREF="images/m7a14b958.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/m7a14b958.gif" NAME="Объект118" ALIGN=ABSMIDDLE WIDTH=259 HEIGHT=46></A>,<P>
где
<A HREF="images/m2071f23a.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/m2071f23a.gif" NAME="Объект119" ALIGN=ABSMIDDLE WIDTH=17 HEIGHT=18></A><FONT FACE="Symbol">&#;</FONT>
произвольно малое фиксированное положительное число.<P>
Теоремы 2<FONT FACE="Symbol">&#;</FONT>4
относятся к случаю
<A HREF="images/4a4d357e.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/4a4d357e.gif" NAME="Объект120" ALIGN=ABSMIDDLE WIDTH=46 HEIGHT=18></A>.<P>
Рассмотрим теперь задачу о натуральных числах
<A HREF="images/2b4aa810.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/2b4aa810.gif" NAME="Объект121" ALIGN=ABSMIDDLE WIDTH=27 HEIGHT=18></A>,
представимых в форме
<A HREF="images/48196b71.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/48196b71.gif" NAME="Объект122" ALIGN=ABSMIDDLE WIDTH=50 HEIGHT=20></A>,
где
<A HREF="images/496b3a1e.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/496b3a1e.gif" NAME="Объект123" ALIGN=ABSMIDDLE WIDTH=19 HEIGHT=18></A>
и
<A HREF="images/2f7bd377.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/2f7bd377.gif" NAME="Объект124" ALIGN=ABSMIDDLE WIDTH=15 HEIGHT=18></A>
заданные целые числа,
<A HREF="images/m2ef8856b.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/m2ef8856b.gif" NAME="Объект125" ALIGN=ABSMIDDLE WIDTH=18 HEIGHT=18></A>
и
<A HREF="images/32be125.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/32be125.gif" NAME="Объект126" ALIGN=ABSMIDDLE WIDTH=18 HEIGHT=18></A>
натуральные числа
<A HREF="images/3a311a09.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/3a311a09.gif" NAME="Объект127" ALIGN=ABSMIDDLE WIDTH=33 HEIGHT=18></A>,
причем
<A HREF="images/47bbe40a.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/47bbe40a.gif" NAME="Объект128" ALIGN=ABSMIDDLE WIDTH=46 HEIGHT=18></A>.
Применим теорему 1. Главный член в этой теореме равен<P>
<A HREF="images/6e470fc5.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/6e470fc5.gif" NAME="Объект129" ALIGN=ABSMIDDLE WIDTH=396 HEIGHT=130></A><P>
<BR />
<P> Если
<A HREF="images/5043eb8f.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/5043eb8f.gif" NAME="Объект130" ALIGN=ABSMIDDLE WIDTH=65 HEIGHT=22></A>,
<A HREF="images/m5241f5de.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/m5241f5de.gif" NAME="Объект131" ALIGN=ABSMIDDLE WIDTH=61 HEIGHT=22></A>,
то последнее выражение равно<P>
<A HREF="images/m761ac491.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/m761ac491.gif" NAME="Объект132" ALIGN=ABSMIDDLE WIDTH=362 HEIGHT=363></A><P>
Отсюда также, как при доказательстве предыдущей
теоремы, имеем<P>
<A HREF="images/m27c5b601.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/m27c5b601.gif" NAME="Объект133" ALIGN=ABSMIDDLE WIDTH=385 HEIGHT=98></A><P>
Аналогичные равенства справедливы для
<A HREF="images/m2a8de6e2.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/m2a8de6e2.gif" NAME="Объект134" ALIGN=ABSMIDDLE WIDTH=75 HEIGHT=21></A>.<DL>
<DT>
<BR />
<DT>Литература:</DL>
<OL>
<LI><P>
Оразов М. Некоторые приложения неравенства
Романова-Эрдоша.<FONT FACE="Symbol">&#;</FONT>
Изв.АН Туркм.ССР, сер. физ.<FONT FACE="Symbol">&#;</FONT>техн.,
хим. и геолог. Наук 1 (1978), 3<FONT FACE="Symbol">&#;</FONT>9.<LI><P>
<SPAN LANG="sq-AL">Wirzing E. Eine Erweiter und der
esten Romanow schen sotzes.</SPAN><SPAN LANG="sq-AL"><FONT FACE="Symbol">&#;</FONT></SPAN><SPAN LANG="sq-AL">
Math., 9(1958), 407</SPAN><SPAN LANG="sq-AL"><FONT FACE="Symbol">&#;</FONT></SPAN><SPAN LANG="sq-AL">409.</SPAN><LI><P>
Бредихин Б.М. Остаточный член в асимптотической формуле
для
<A HREF="images/m73454fe4.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/m73454fe4.gif" NAME="Объект135" ALIGN=ABSMIDDLE WIDTH=55 HEIGHT=20></A>.<FONT FACE="Symbol">&#;</FONT>
Изв. Высших учебных заведений СССР, Математика, 6(19), 1960, 40<FONT FACE="Symbol">&#;</FONT>49.</OL>
<DIV TYPE=FOOTER>
<P><BR />
</DIV>
