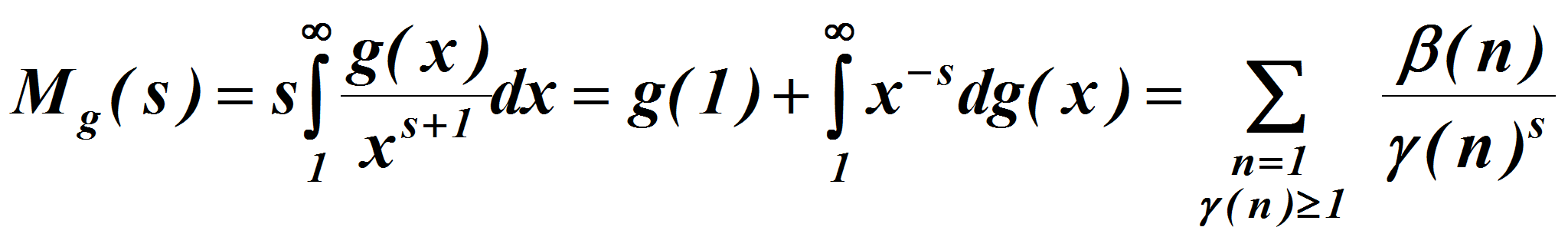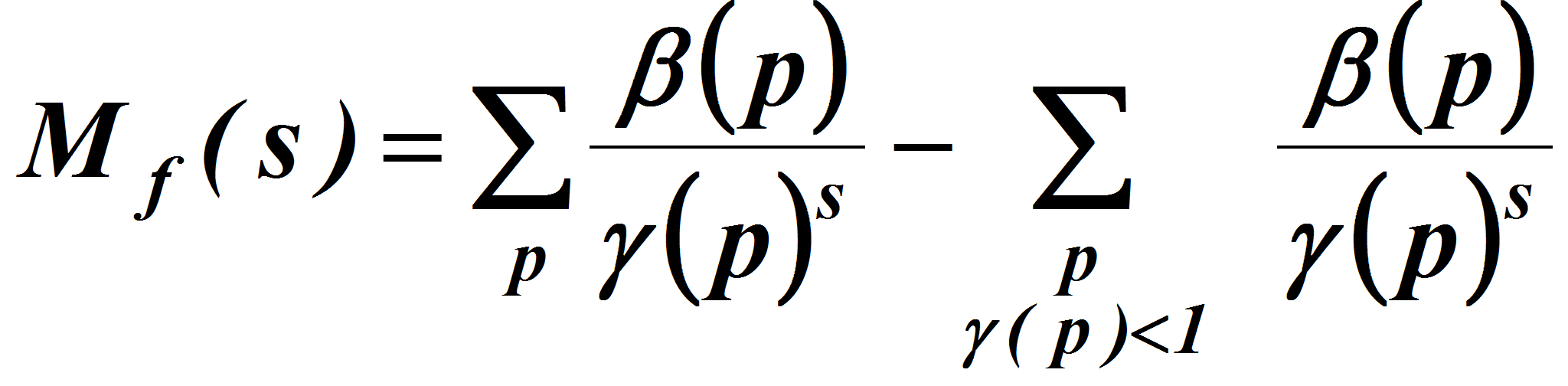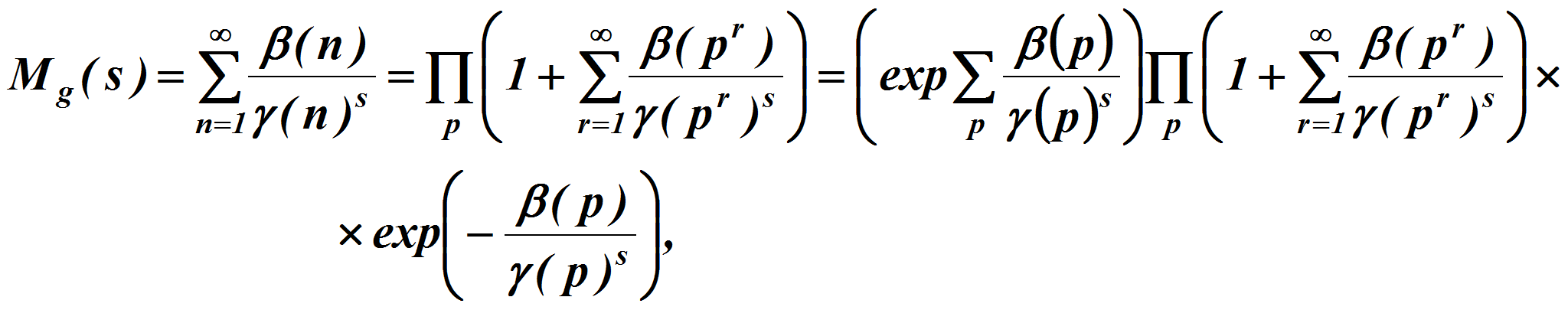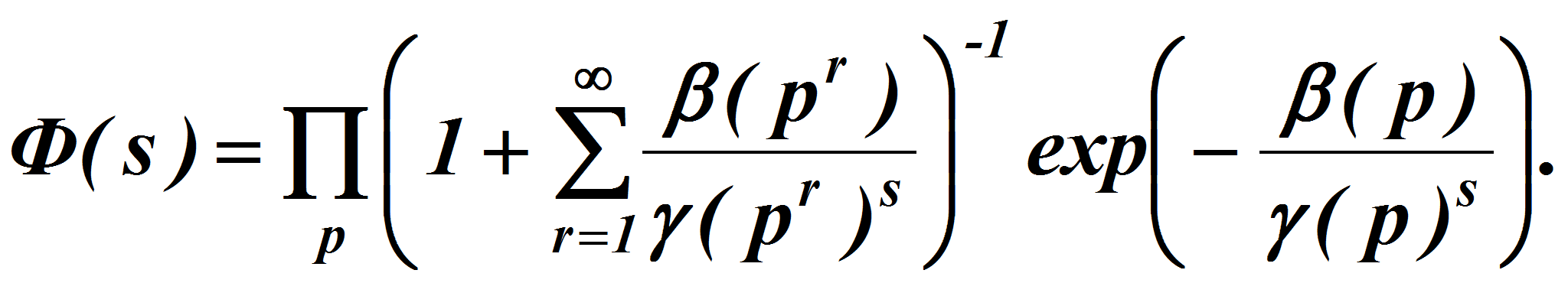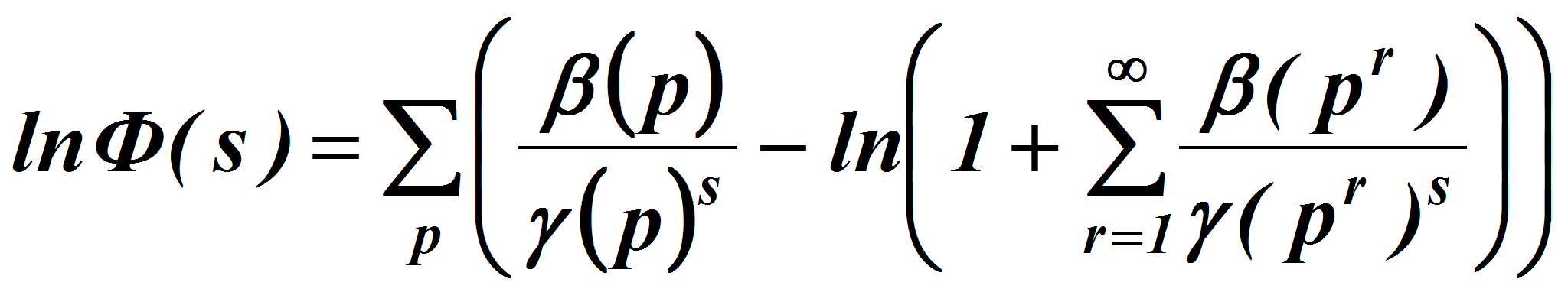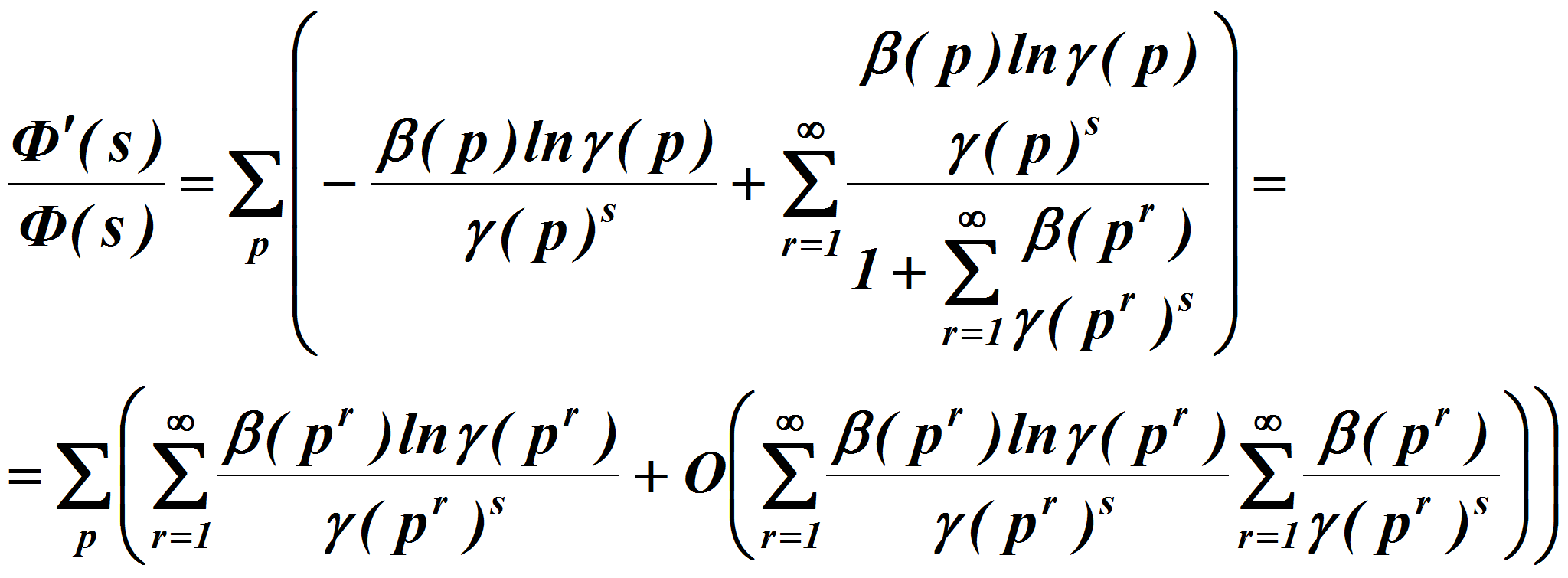The work is devoted to the issue surrounding the symptotic behaviour of sum of values of multiplicative functions. A connection is identified between such sums for prime numbers and natural numbers.
The results obtained during the work process are based on research of analytical properties of specified sums and can be applied to the theory of free normative semi-groups.
Работа посвящена задачам, где изучается асимптотическое поведение суммы значений мультипликативных функций. Устанавливается связь между такими суммами по простым числам и натуральным числам.
Результаты, полученные в работе, основаны на исследовании аналитических свойств указанных сумм и имеют приложения в теории свободных нормированных полугрупп.
Пусть
и
− неотрицательные мультипликативные функции. Определим функции
и
следующим образом:
,
(
− простые числа,
−
натуральные числа).
Введем обозначения
;
.
Учитывая определения функции
и
имеем
;
.
Откуда
;
.
Предположим, что ряд
сходится в полуплоскости
.
Начиная с этого момента, мы предполагаем также, что
для всех натуральных
.
Так как все члены ряда
неотрицательные числа, то отсюда следует, что ряд для
(а
следовательно и ряд для
)
при
сходится абсолютно.
Так как для любого фиксированного
функция
мультипликативна по
,
то в силу тождества Эйлера для мультипликативных функций имеем:
откуда
- где
-
Чтобы получить намеченный результат мы должны обеспечить
равномерную продолжимость производной
на прямую
.
Для этого во всяком случае необходимо чтобы каждый из рядов
сходился и чтобы при
было справедливо неравенство
.
Это условие будет выполнено, если мы потребуем, чтобы
для всех простых
выполнялось неравенство
.
(1)
Действительно, в этом случае
.
Далее
,
откуда
(2)
Отсюда видно, что если наряду с условием (2) потребовать сходимость рядов
и
,
то это обеспечит равномерную продолжимость функции
(а значит функции
)
на прямую
.
Теорема 1. Пусть
и
−
неотрицательные мультипликативные функции, причем
для всех
.
,
,
,
Тогда если ряды
и
сходятся и
для всех
,
то
.
(доказательство теоремы из-за громоздких вычислений не приводится).
Рассмотрим несколько следствий теоремы 1.
Следствие 1. Пусть
&#;
неотрицательная мультипликативная функция
,
,
.
Если ряды
и
сходятся и
для всех простых
,
то
.
В частности, этим условиям удовлетворяет функция
.
Поэтому отсюда следует закон простых чисел.
Следствие 2. Пусть
&#;</FONT>
мультипликативная функция,
<A HREF="images/41792d49.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/41792d49.gif" NAME="Объект70" ALIGN=ABSMIDDLE WIDTH=57 HEIGHT=20></A>
для всех неотрицательных
<A HREF="images/mf0fa213.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/mf0fa213.gif" NAME="Объект71" ALIGN=ABSMIDDLE WIDTH=18 HEIGHT=18></A>.<P>
<A HREF="images/m229802b9.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/m229802b9.gif" NAME="Объект72" ALIGN=ABSMIDDLE WIDTH=181 HEIGHT=47></A>,
<A HREF="images/6f67ba9f.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/6f67ba9f.gif" NAME="Объект73" ALIGN=ABSMIDDLE WIDTH=39 HEIGHT=18></A>,
<A HREF="images/m358502df.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/m358502df.gif" NAME="Объект74" ALIGN=ABSMIDDLE WIDTH=39 HEIGHT=18></A>.<P>
Тогда если ряды
<P>
<A HREF="images/m24a70a01.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/m24a70a01.gif" NAME="Объект75" ALIGN=ABSMIDDLE WIDTH=109 HEIGHT=45></A>
и
<A HREF="images/38552012.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/38552012.gif" NAME="Объект76" ALIGN=ABSMIDDLE WIDTH=81 HEIGHT=41></A>
<P>сходятся и
<P>
<A HREF="images/m5a3de862.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/m5a3de862.gif" NAME="Объект77" ALIGN=ABSMIDDLE WIDTH=94 HEIGHT=45></A>
для всех простых
<A HREF="images/m66aee3d2.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/m66aee3d2.gif" NAME="Объект78" ALIGN=ABSMIDDLE WIDTH=20 HEIGHT=18></A>,
<P>то<P>
<A HREF="images/731bd49c.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/731bd49c.gif" NAME="Объект79" ALIGN=ABSMIDDLE WIDTH=98 HEIGHT=41></A>.<P>
<I><B>Замечания.</B></I>
<OL><LI><P>
В формулировке теоремы 1 и ее следствий условие</OL>
<P>
<A HREF="images/m6ab1b35e.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/m6ab1b35e.gif" NAME="Объект80" ALIGN=ABSMIDDLE WIDTH=203 HEIGHT=47></A>,
<A HREF="images/6f67ba9f.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/6f67ba9f.gif" NAME="Объект81" ALIGN=ABSMIDDLE WIDTH=39 HEIGHT=18></A>,
<A HREF="images/m358502df.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/m358502df.gif" NAME="Объект82" ALIGN=ABSMIDDLE WIDTH=39 HEIGHT=18></A>
(3)<P>
можно заменить более слабым ограничением<P>
<A HREF="images/70af085c.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/70af085c.gif" NAME="Объект83" ALIGN=ABSMIDDLE WIDTH=154 HEIGHT=34></A>,
<A HREF="images/6f67ba9f.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/6f67ba9f.gif" NAME="Объект84" ALIGN=ABSMIDDLE WIDTH=39 HEIGHT=18></A>,
<P>
<A HREF="images/2dd707c8.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/2dd707c8.gif" NAME="Объект85" ALIGN=ABSMIDDLE WIDTH=138 HEIGHT=48></A>.<P>
Так, например, в условии (3) достаточно иметь остаточный
член<P>
<A HREF="images/1d10a908.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/1d10a908.gif" NAME="Объект86" ALIGN=ABSMIDDLE WIDTH=136 HEIGHT=47></A>,
<A HREF="images/m358502df.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/m358502df.gif" NAME="Объект87" ALIGN=ABSMIDDLE WIDTH=39 HEIGHT=18></A>.<P>
2. Вместо неравенства<P>
<A HREF="images/m665bd15d.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/m665bd15d.gif" NAME="Объект88" ALIGN=ABSMIDDLE WIDTH=97 HEIGHT=45></A><P>
достаточно потребовать, чтобы при
<A HREF="images/4e7e5d87.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/4e7e5d87.gif" NAME="Объект89" ALIGN=ABSMIDDLE WIDTH=40 HEIGHT=18></A>
при любых простых
<A HREF="images/m66aee3d2.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/m66aee3d2.gif" NAME="Объект90" ALIGN=ABSMIDDLE WIDTH=20 HEIGHT=18></A>
выполнялось условие<P>
<A HREF="images/7ea8c6f.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/7ea8c6f.gif" NAME="Объект91" ALIGN=ABSMIDDLE WIDTH=109 HEIGHT=45></A>.
(4)<P>
Последнее замечание играет роль в некоторых важных
частных случаях. Пусть, например, в условиях теоремы 1 функции
<A HREF="images/612ec380.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/612ec380.gif" NAME="Объект92" ALIGN=ABSMIDDLE WIDTH=39 HEIGHT=20></A>
и
<A HREF="images/m7812c6e0.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/m7812c6e0.gif" NAME="Объект93" ALIGN=ABSMIDDLE WIDTH=36 HEIGHT=20></A>
вполне мультипликативны. Тогда условие (4) означает, что<P>
<A HREF="images/m596a1dbb.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/m596a1dbb.gif" NAME="Объект94" ALIGN=ABSMIDDLE WIDTH=220 HEIGHT=48></A>,<P>
что выполняется автоматически, поскольку
<A HREF="images/55c43501.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/55c43501.gif" NAME="Объект95" ALIGN=ABSMIDDLE WIDTH=65 HEIGHT=23></A>,
если только
<A HREF="images/5be8c66a.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/5be8c66a.gif" NAME="Объект96" ALIGN=ABSMIDDLE WIDTH=84 HEIGHT=20></A>
для всех простых
<A HREF="images/m66aee3d2.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/m66aee3d2.gif" NAME="Объект97" ALIGN=ABSMIDDLE WIDTH=20 HEIGHT=18></A>.<P>
Кроме того, в этом случае<P>
<A HREF="images/6755b98e.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/6755b98e.gif" NAME="Объект98" ALIGN=ABSMIDDLE WIDTH=340 HEIGHT=97></A><P>
Таким образом справедлива следующая<P>
<I><B>Теорема 2.</B></I> Пусть
<A HREF="images/28709dc2.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/28709dc2.gif" NAME="Объект99" ALIGN=ABSMIDDLE WIDTH=39 HEIGHT=20></A>
и
<A HREF="images/5232127.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/5232127.gif" NAME="Объект100" ALIGN=ABSMIDDLE WIDTH=39 HEIGHT=18></A>−
неотрицательные, вполне мультипликативные функции,
<A HREF="images/1007a8cb.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/1007a8cb.gif" NAME="Объект101" ALIGN=ABSMIDDLE WIDTH=147 HEIGHT=18></A>
при всех простых
<A HREF="images/m66aee3d2.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/m66aee3d2.gif" NAME="Объект102" ALIGN=ABSMIDDLE WIDTH=20 HEIGHT=18></A>.<P>
<A HREF="images/28020ad6.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/28020ad6.gif" NAME="Объект103" ALIGN=ABSMIDDLE WIDTH=201 HEIGHT=47></A>,
<A HREF="images/6f67ba9f.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/6f67ba9f.gif" NAME="Объект104" ALIGN=ABSMIDDLE WIDTH=39 HEIGHT=18></A>,
<A HREF="images/m358502df.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/m358502df.gif" NAME="Объект105" ALIGN=ABSMIDDLE WIDTH=39 HEIGHT=18></A>,
(5)<P>
Тогда если ряд<P>
<A HREF="images/m65f79e67.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/m65f79e67.gif" NAME="Объект106" ALIGN=ABSMIDDLE WIDTH=124 HEIGHT=44></A>
<P>сходится, то<P>
<A HREF="images/m5764b518.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/m5764b518.gif" NAME="Объект107" ALIGN=ABSMIDDLE WIDTH=120 HEIGHT=42></A>.<P>
Пусть
<A HREF="images/7fcd3607.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/7fcd3607.gif" NAME="Объект108" ALIGN=ABSMIDDLE WIDTH=22 HEIGHT=18></A><FONT FACE="Symbol">&#;</FONT>
любое фиксированное натуральное число, тогда из условия (5) следует<P>
<A HREF="images/m2683b1f1.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/m2683b1f1.gif" NAME="Объект109" ALIGN=ABSMIDDLE WIDTH=320 HEIGHT=51></A>,
<P>откуда<P>
<A HREF="images/m850cabf.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/m850cabf.gif" NAME="Объект110" ALIGN=ABSMIDDLE WIDTH=161 HEIGHT=51></A>
<P>для любого натурального
<A HREF="images/7fcd3607.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/7fcd3607.gif" NAME="Объект111" ALIGN=ABSMIDDLE WIDTH=22 HEIGHT=18></A>.<P>
Поэтому<P>
<A HREF="images/m11fa9bb4.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/m11fa9bb4.gif" NAME="Объект112" ALIGN=ABSMIDDLE WIDTH=369 HEIGHT=191></A><P>
Отсюда следует, что ряд<P>
<A HREF="images/51834253.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/51834253.gif" NAME="Объект113" ALIGN=ABSMIDDLE WIDTH=122 HEIGHT=45></A><P>
сходится и тем более сходится ряд по простым числам.<P>
Поэтому из теоремы 2 вытекает<P>
<BR />
<P><I><B>Теорема 3.</B></I>
Пусть
<A HREF="images/28709dc2.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/28709dc2.gif" NAME="Объект114" ALIGN=ABSMIDDLE WIDTH=39 HEIGHT=20></A>
и
<A HREF="images/5232127.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/5232127.gif" NAME="Объект115" ALIGN=ABSMIDDLE WIDTH=39 HEIGHT=18></A>−
неотрицательные мультипликативные функции,
<A HREF="images/1007a8cb.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/1007a8cb.gif" NAME="Объект116" ALIGN=ABSMIDDLE WIDTH=147 HEIGHT=18></A>
для всех простых
<A HREF="images/m66aee3d2.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/m66aee3d2.gif" NAME="Объект117" ALIGN=ABSMIDDLE WIDTH=20 HEIGHT=18></A>
и выполнено условие (5).<P>
Тогда
<P>
<A HREF="images/m5764b518.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/m5764b518.gif" NAME="Объект118" ALIGN=ABSMIDDLE WIDTH=120 HEIGHT=42></A>.<DL>
<DT>
Литература:</DL>
<OL>
<LI><P>
Файнлейб А.С. Некоторые асимптотические формулы для
сумм мультипликативных функций и их приложения.<FONT FACE="Symbol">&#;</FONT>
Литовский матем. сборник, 7, №13, 1967, 535-545.<LI><P>
Ингам А.Е. Распределение простых чисел.<FONT FACE="Symbol">&#;</FONT>
ОНТИ, 1936.<LI><P>
Титчмарш Е.К. Теория дзета-функции Римана.<FONT FACE="Symbol">&#;</FONT>
ИЛ, 1953.</OL>
