В работах [1, 2] для управления движением механической системы в качестве исполнительного элемента была выбрана бесколлекторная электрическая машина (ЭМ) постоянного тока и динамику последних описывали уравнениями работ Львовича А. Ю. [3; 4], Лурье А. И. и Ходжаева Ш. С. [5], Борцова Ю. А. [6]. Однако, в промышленности широкое применение находят и коллекторные электрические машины ЭМ. Например, как утверждают Кенио Т. и Нагамори С. [7], их используют в электроприводах тонвалов проигрывателей, магнитофонов и видеомагнитофонов, объективов камер с переменным фокусным расстоянием и т. д. Коллекторная электрическая машина (ЭМ) может быть рассмотрена как объемные проводники со скользящими контактами. При вращении якоря электрической машины ЭМ в системе осуществляются неголономные связи, и уравнения движения таких систем могут быть описаны уравнениями Гапонова А. В., приведенные в работах Гапонова А. В. [8], Неймарка Ю. И. и Фуфаева Н. А. [9]. Преимуществом этих уравнений является то, что уравнения неголономных связей в уравнения электрической машины ЭМ не входят. Уравнения Гапонова А. В. для электрической машины ЭМ постоянного тока с независимым возбуждением и управляемым якорным напряжением, могут быть записаны в виде:

,

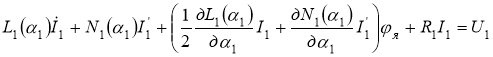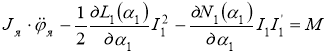(1)

Где N₁(₁) — коэффициент взаимоиндукции; _{1 —} угол между магнитной осью и линией коллекторных щеток и знак штрих относится к соответствующим параметрам статора.

Если для управления движением механической системы вместо бесколлекторных электрических машин использовать коллекторные, математическую модель которых описывали уравнениями (1), то уравнения (2)-(3) будут иметь вид:

,

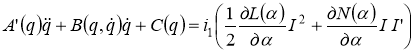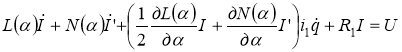,(2)

Где I, I’ – матрицы столбцы токов; , L, N, R – диагональные матрицы.

В системе (2) можно принять:, так как, подавая на обмотку возбуждения постоянный ток и постоянное напряжение, мы регулируем угловую скорость якоря путем регулирования напряжения, подаваемого на обмотку якоря.

Если принять: _y=0, _э=(L/R)=0, то придем к той же упрощенной модели электромеханической системы, которую рассматривали в работе.

Если же учесть индуктивность якоря, т. е. _’=0, то придем к некоторому изменению закона формирования управляющих напряжений. Из второго уравнения (2) определив I, т. е.

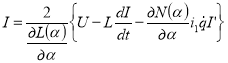
и подставив последнее выражение в первое уравнение названной системы уравнений (2), получим:

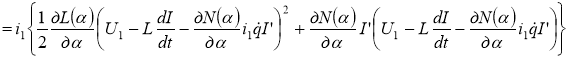
или

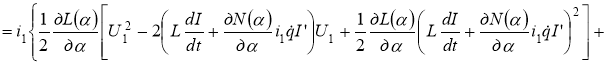
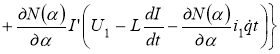
Если, как и в § 1.2, на задающем устройстве управляющие напряжения формировать по закону:

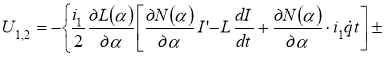
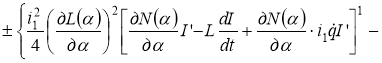
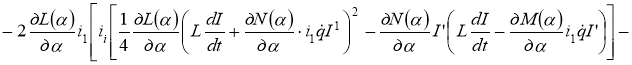
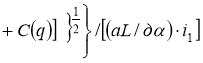,(3)

тогда переходный процесс будет характеризоваться уравнением:

, и, следовательно, условия устойчивого осуществления заранее заданного движения q^o(t) имеют вид

h_je>0,(j=1,…,n;e=0,…,1)

Но здесь возникают некоторые неудобства в случае, когда выражение, стоящее под корнем закона изменения напряжения (3), станет отрицательной. В этом случае получим комплексные напряжения, которые для электрических машин постоянного тока не имеют места.

Вообще, во избежание ошибок и громоздких вычислений, целесообразно использовать упрощенную модель, которая, как уже видели, вполне применима.

Литература:

1. Тешаев М. Х. Об осуществлении сервосвязей электромеханической следящей системой/Изв. Вузов. Математика. 2010, № 12. – С. 44–51, Англоязычная версия:RussianMathematics (IzvestiyaVUZ. Matematika), 2010, 54:12, 38–44.
2. Тешаев М. Х. О реализации геометрических сервосвязей электромеханическими силами/ ДАН РУз, С. матем., техн. науки, естесвозн. № 11, 2000. – С. 28–30.
3. Львович А. Ю., Поляхов Н. Н. Основы теории электромеханических систем, — Л.: изд-во ЛГУ, 1973. — 204 с.
4. Львович А. Ю. Электромеханические системы. Учебное пособие. — Л.: изд-во ЛГУ, 1989. — 296 с.
5. Лурье А. И., Ходжаев Ш. С. Уравнение Лагранжа — Максвелла в курсе теоретической механики // Сборник научно-методических статей по теоретической механике. Изд-во АН СССР, 1975. – С. 61–68.
6. Борцов Ю. А. и др. Электромеханические системы с адаптивным и модальным управлением. — Л.: Энергоатомиздат, 1984. – 216 с.
7. Кенио Т., Нагамори С. Двигатели постоянного тока с постоянными магнитами. М.: Энергия, 1990. – 184 с.
8. Гапонов А. П. Электромеханические системы со скользящими контактами и динамическая теория электрических систем // Сб. памяти А. А. Андронова // Изв. АН СССР. 1955. – С. 103–107.
9. Неймарк Ю. И., Фуфаев Н. А. Динамика неголономных систем. — М.: Наука, 1967. – 520 с.