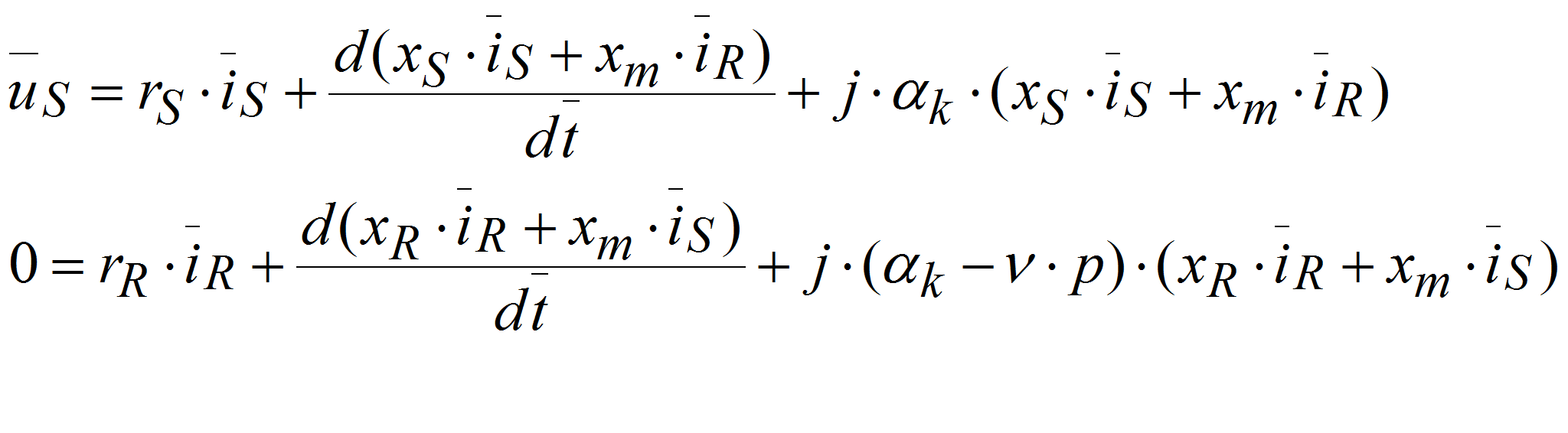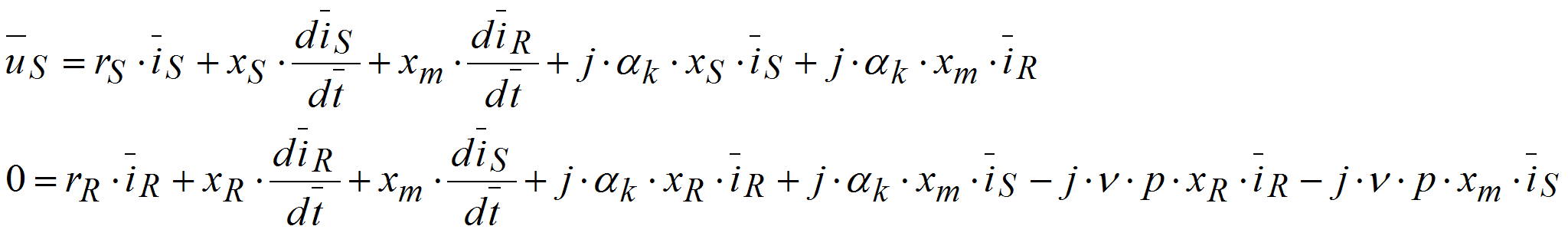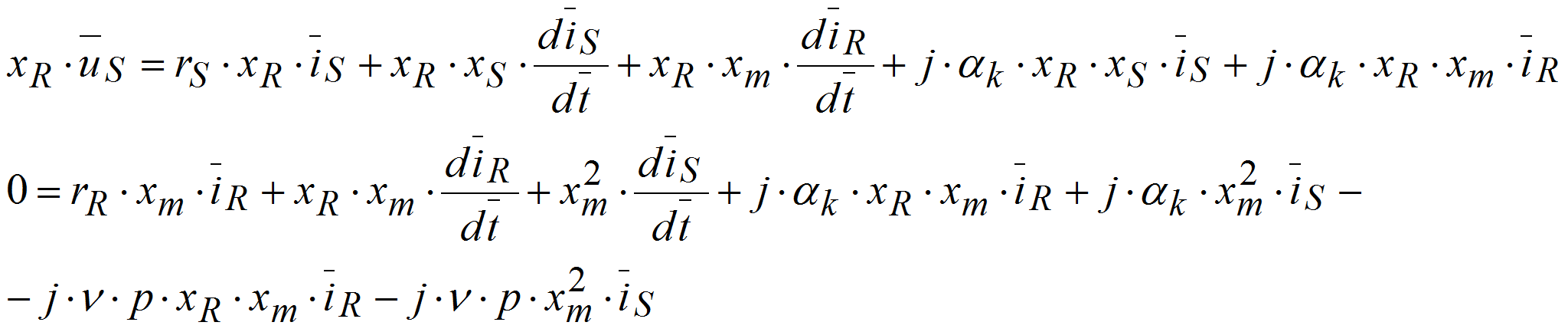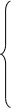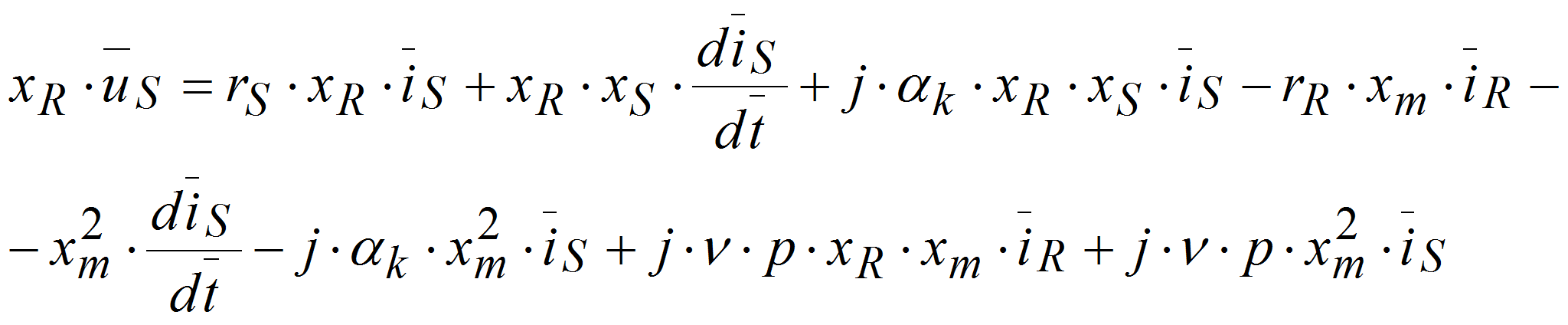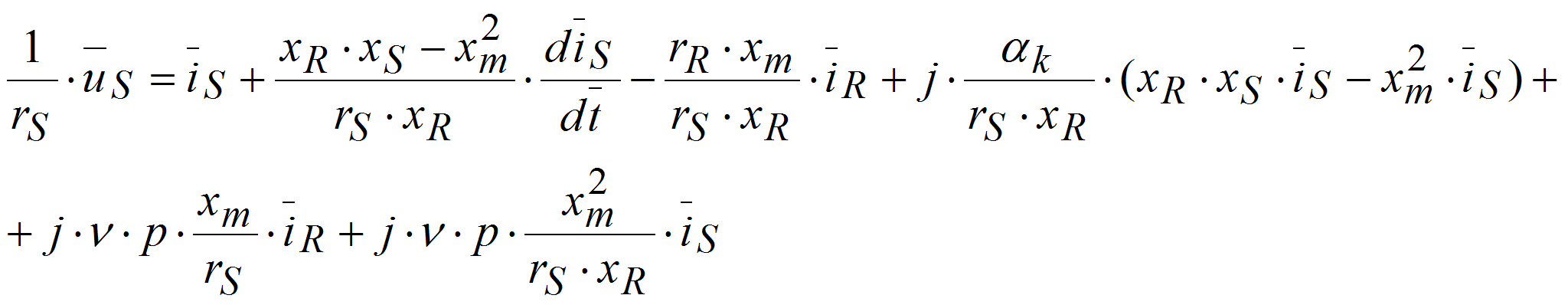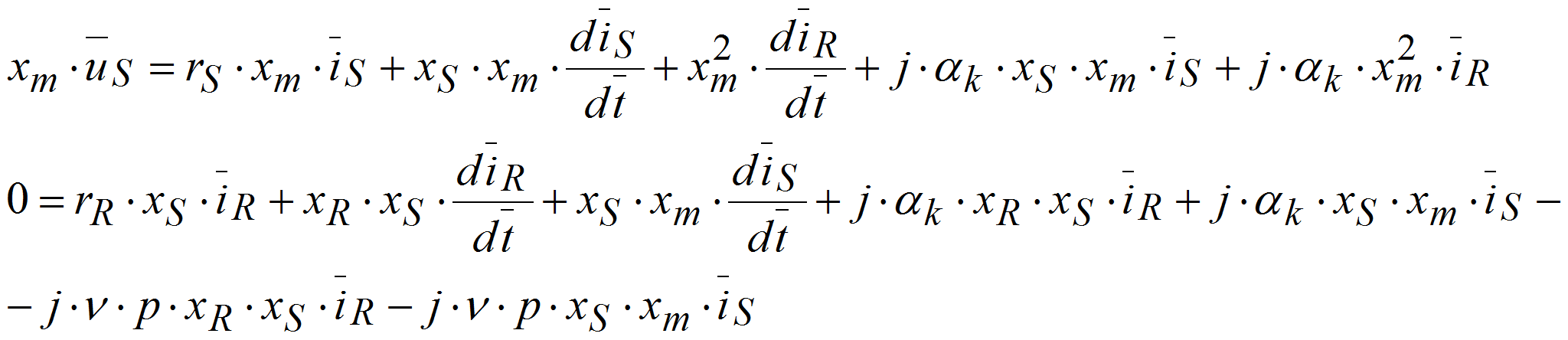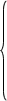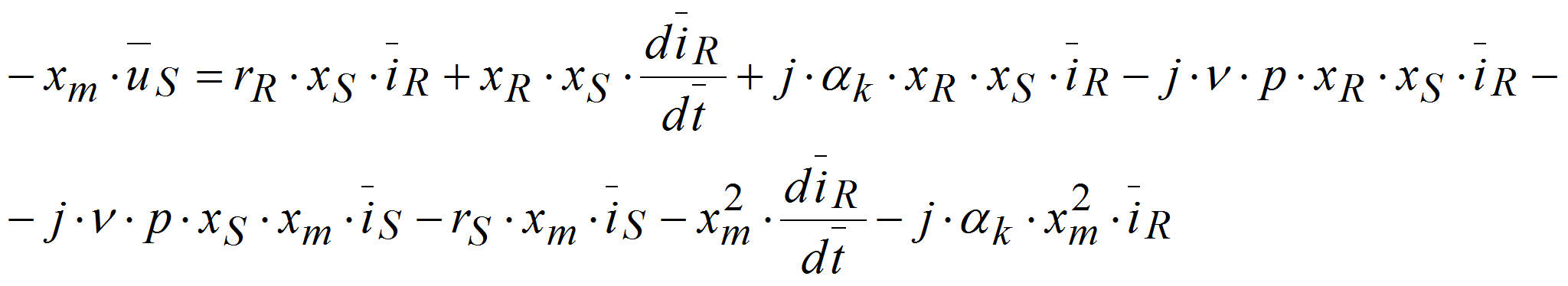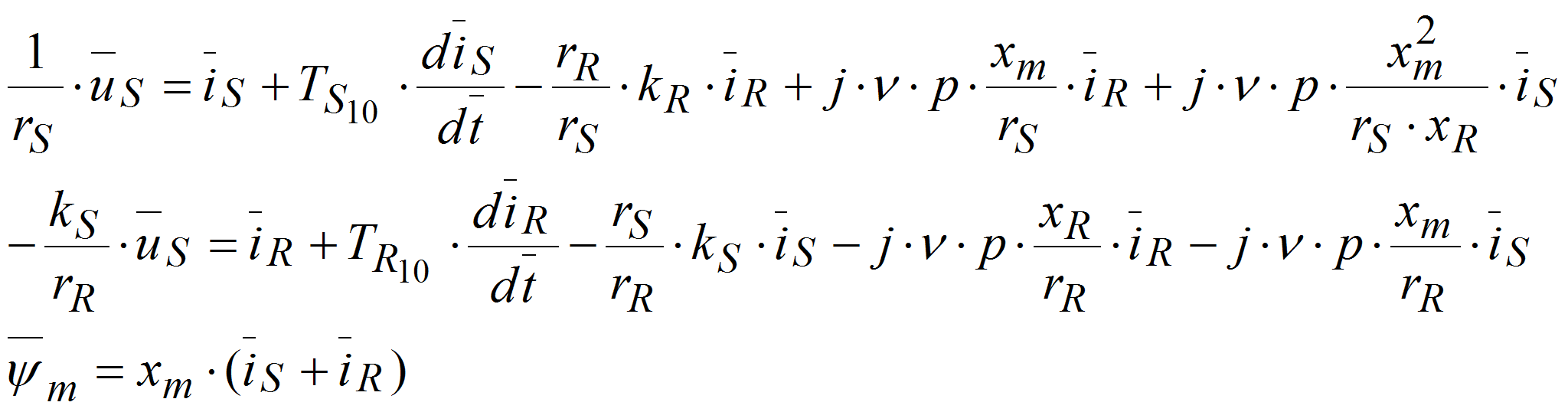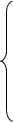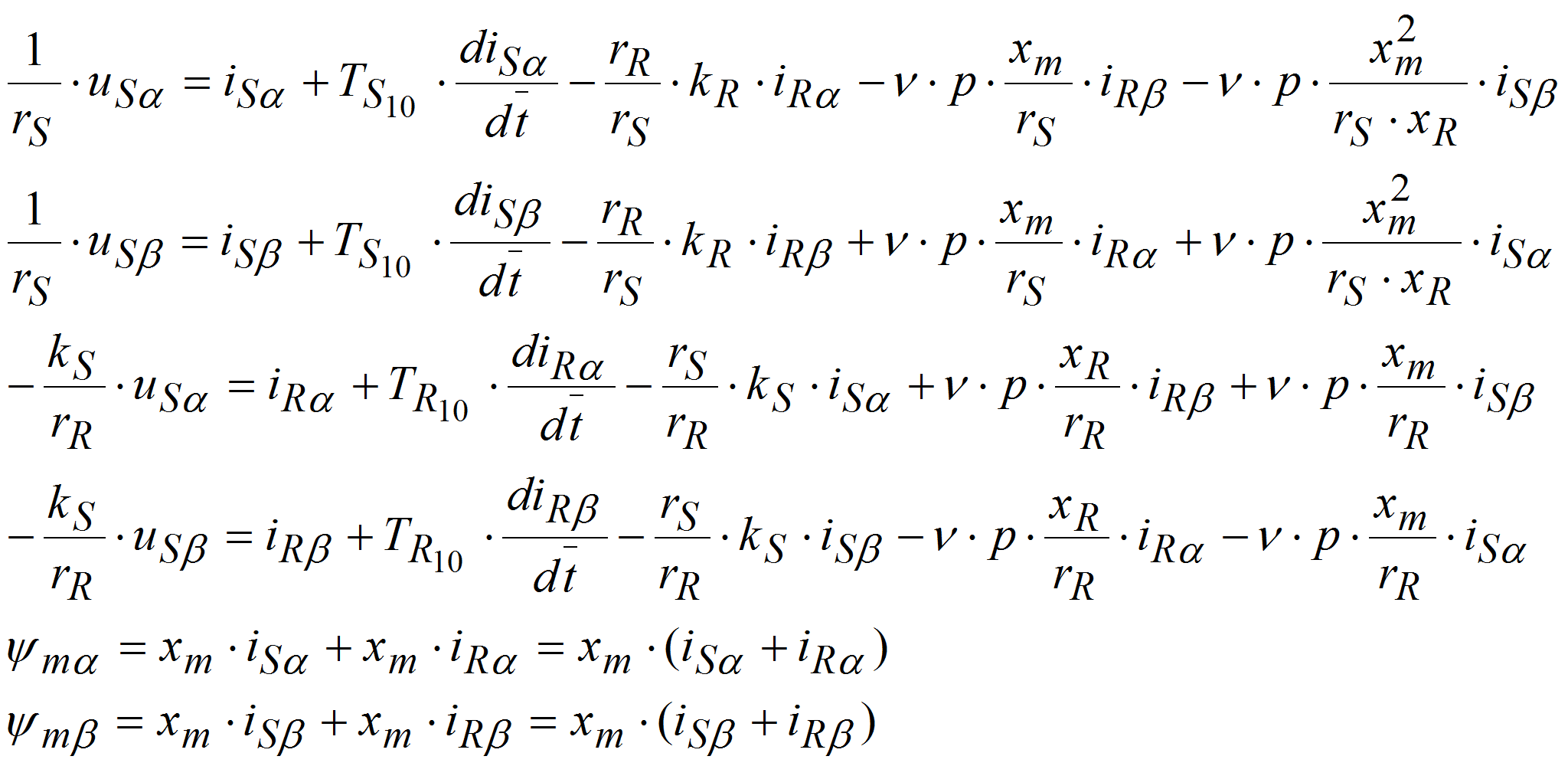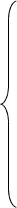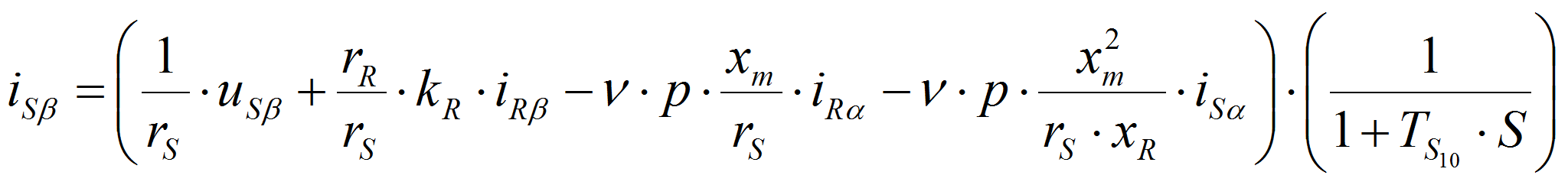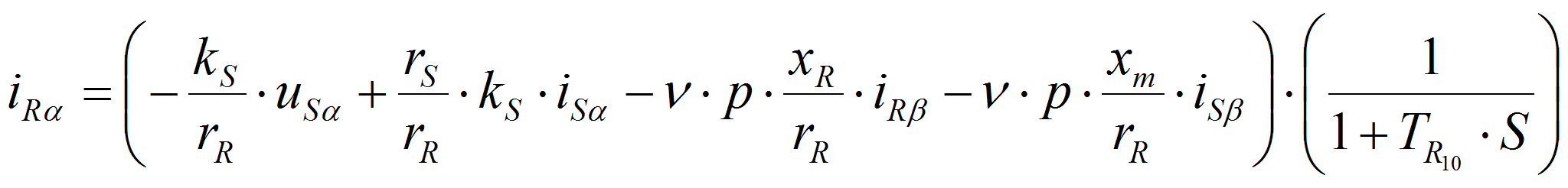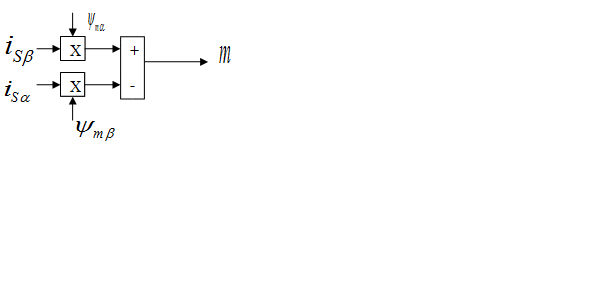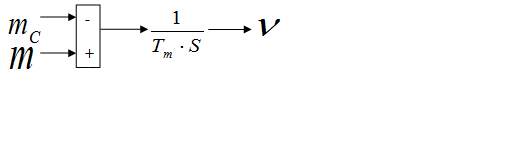При выполнении студентами дипломных и курсовых работ, связанных с моделированием асинхронного двигателя, возникает необходимость увеличения вариантов их модификаций. Одним из способов решения этой задачи является возможность выразить электромагнитный момент через различную комбинацию переменных токов и потокосцеплений двигателя [1, c.238] и [2]. Данная статья позволяет сформировать у студентов представление об одном из множества вариантов моделирования АД в «Matlab-Simulink» и «MathCAD». Вывод уравнений даем без сокращений, т. к. важен не только конечный результат, но и путь, ведущий к цели.
Основные уравнения математической модели АД, записаны в векторной форме в относительных единицах, имеют следующий вид [3]:
- Рассмотрим асинхронный двигатель с К.З. ротором (
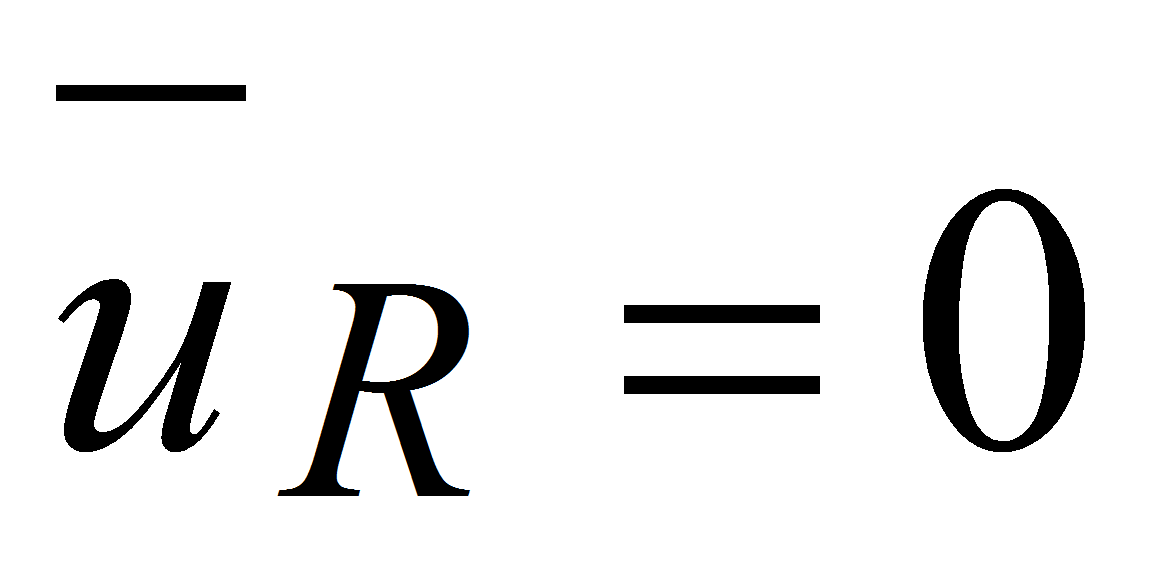 ).
).
- Определим электромагнитный момент по следующей формуле [1, с.238]
-
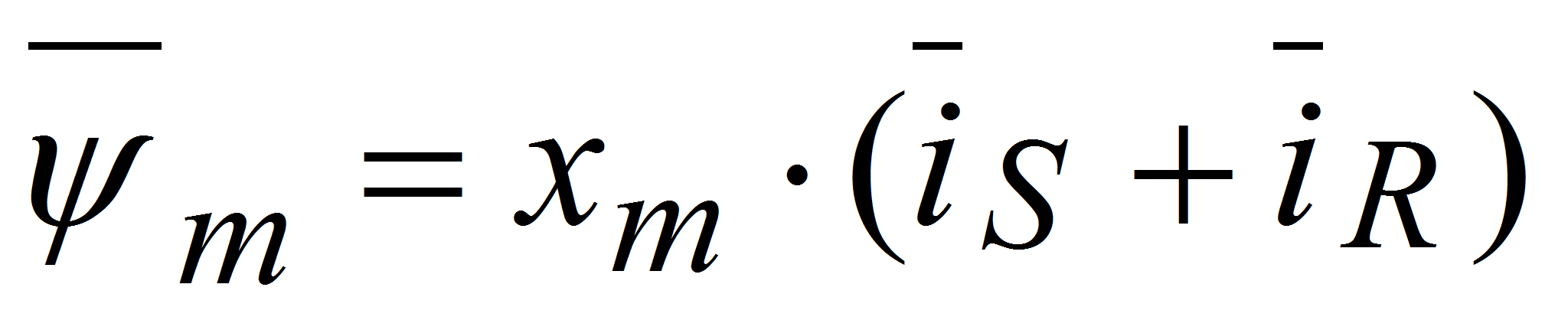
Исключим из системы уравнений
![]() и
и
![]() :
:
- Вычтем второе уравнение из первого:
Разделим обе части уравнения на
![]() :
:
- Тогда уравнение примет вид:
Исключим из системы уравнений
![]() :
:
- Вычтем первое уравнение из второго:
Рассмотрим процессы в неподвижной системе координат,
![]() ,
,
![]() :
:
Вещественную ось обозначим , а мнимую через . Пространственные вектора в этом случае раскладываются по осям:
Подставим эти значения в уравнения и, приравняв отдельно вещественные и мнимые части, получим:
- С учетом электромагнитных моментов система уравнений в
операторной форме
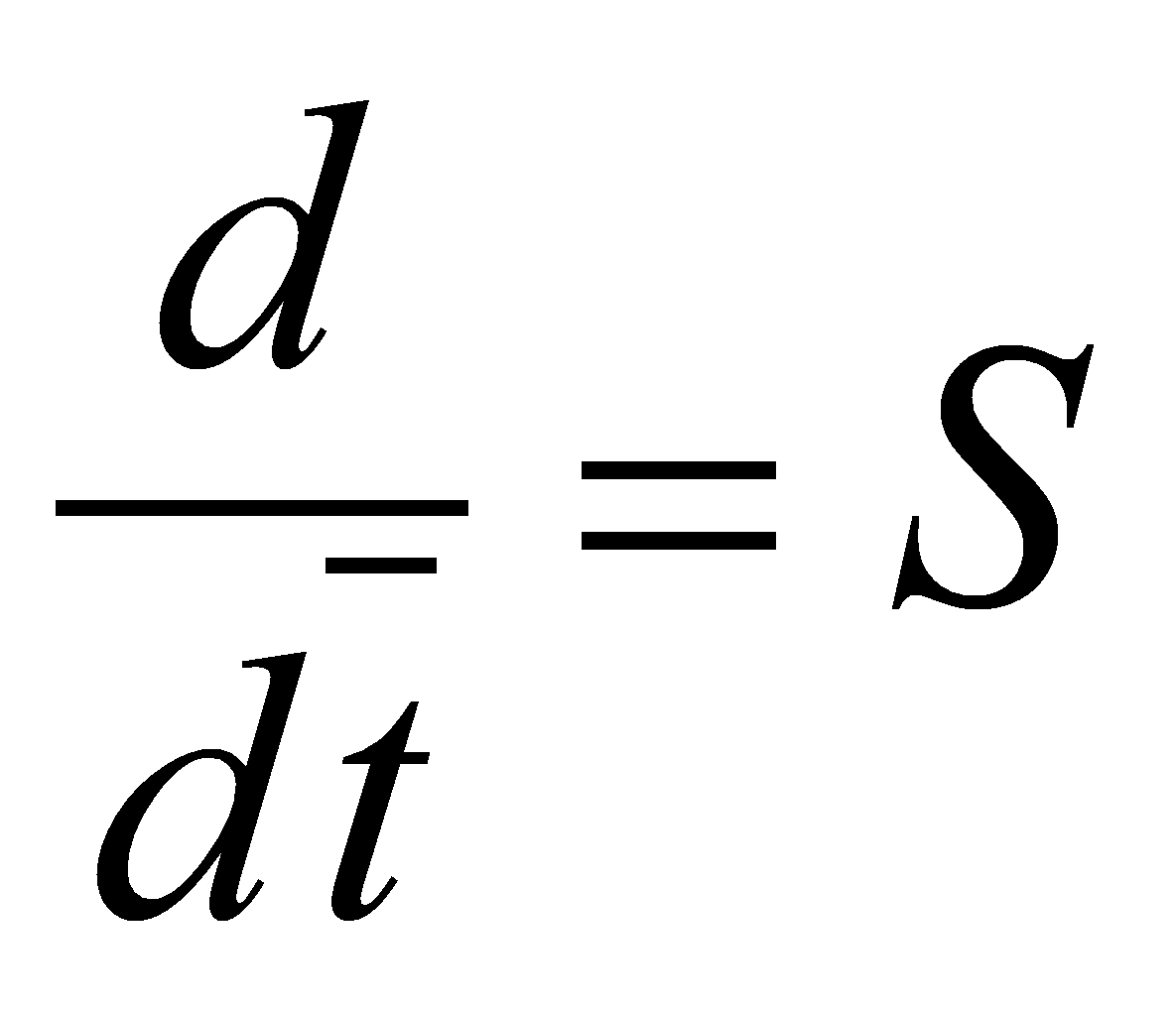 примет вид:
примет вид: -
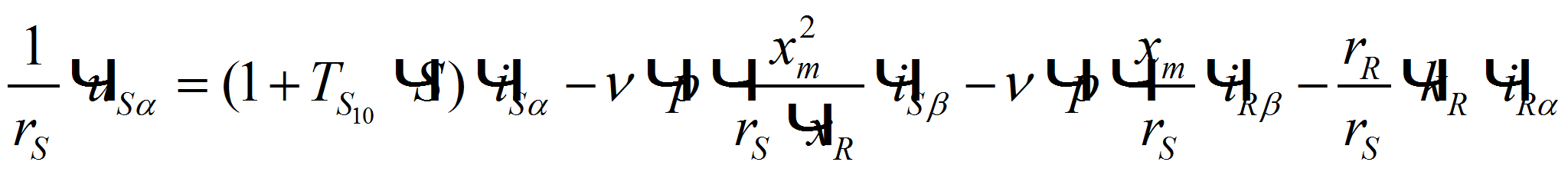
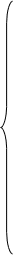 (1)
(1) -
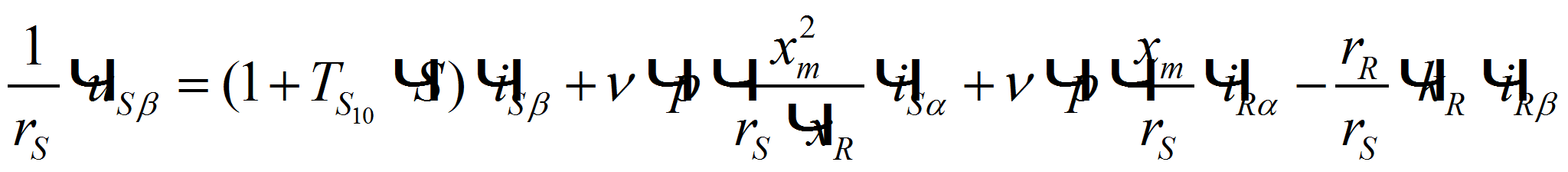 (2)
(2) -
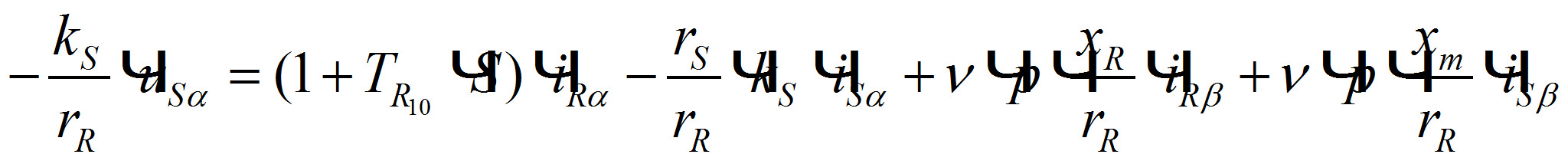 (3)
(3) -
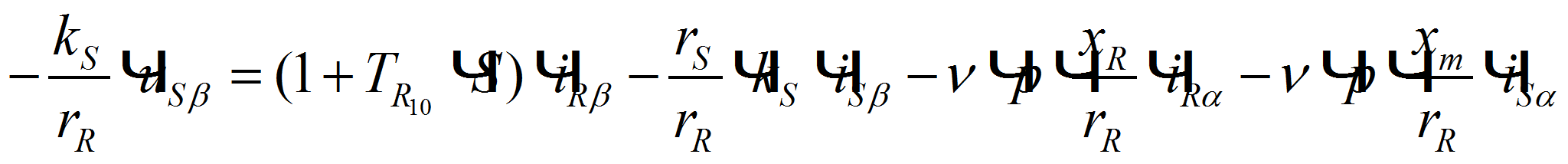 (4)
(4) -
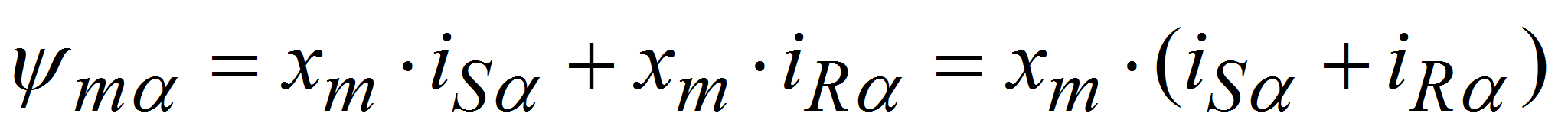 (5)
(5) -
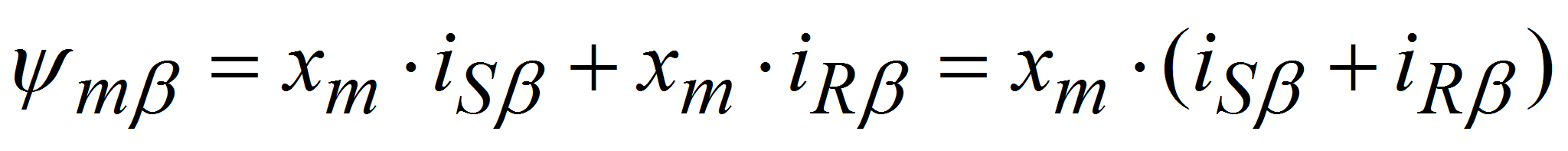 (6)
(6) -
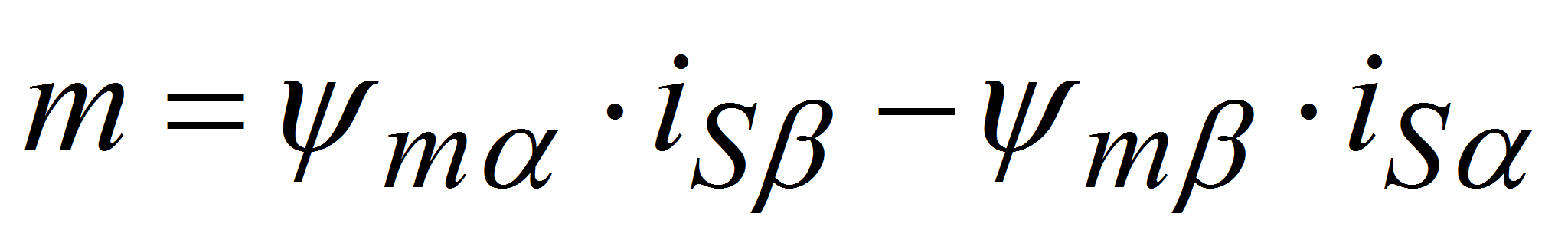 (7)
(7) -
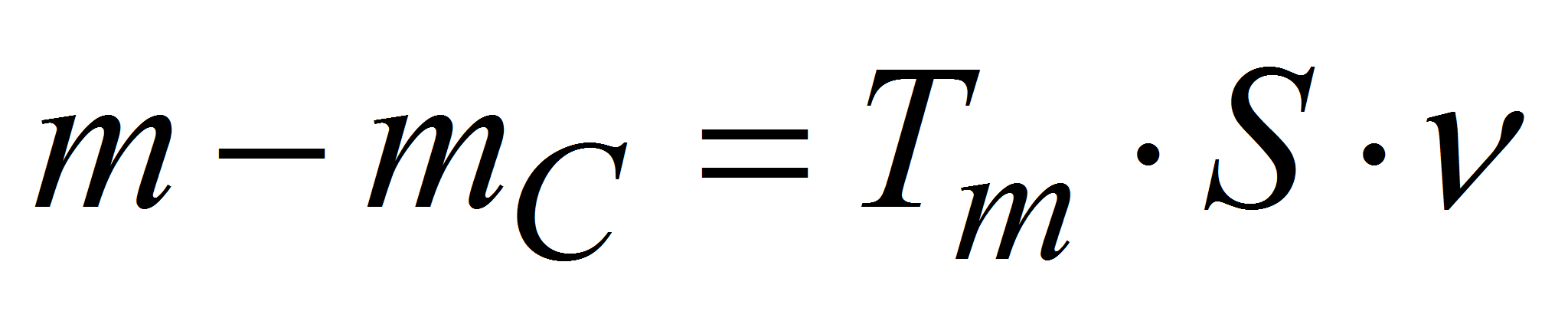 (8)
(8)
Для моделирования выберем АКЗ со следующими паспортными данными и
параметрами:
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
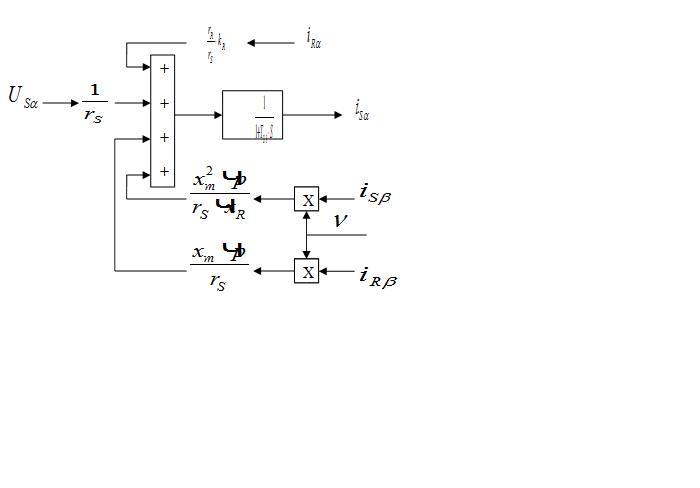
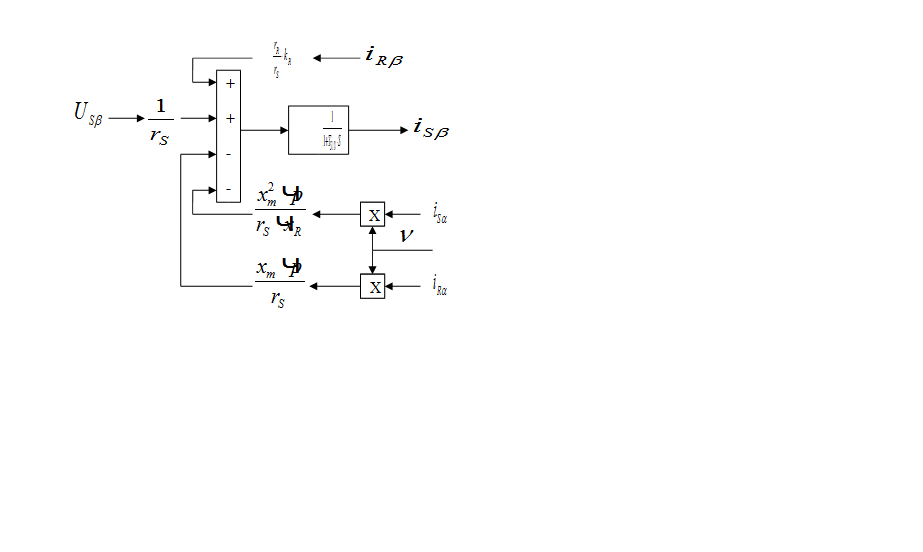
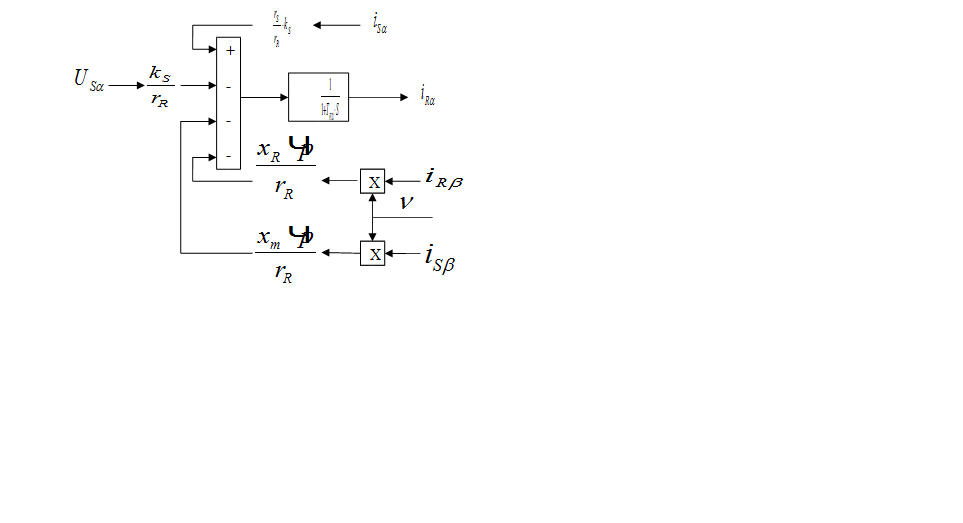
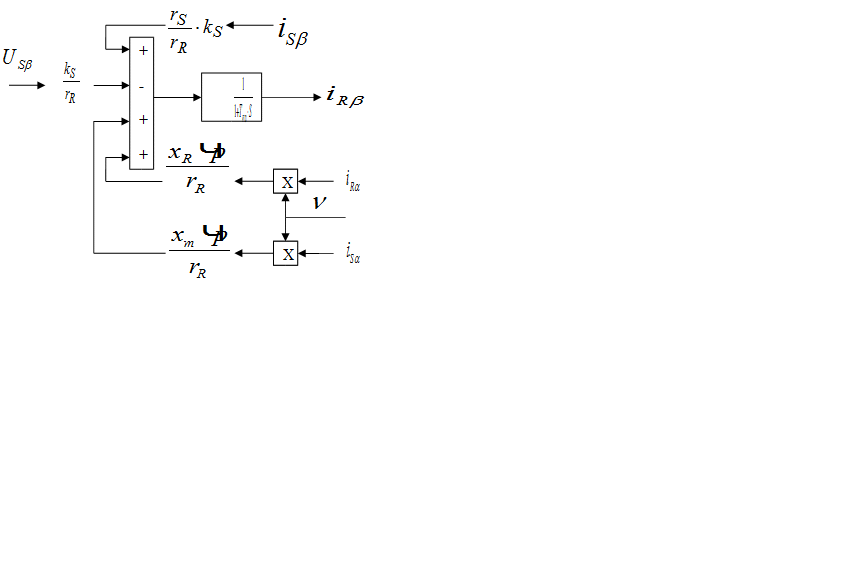
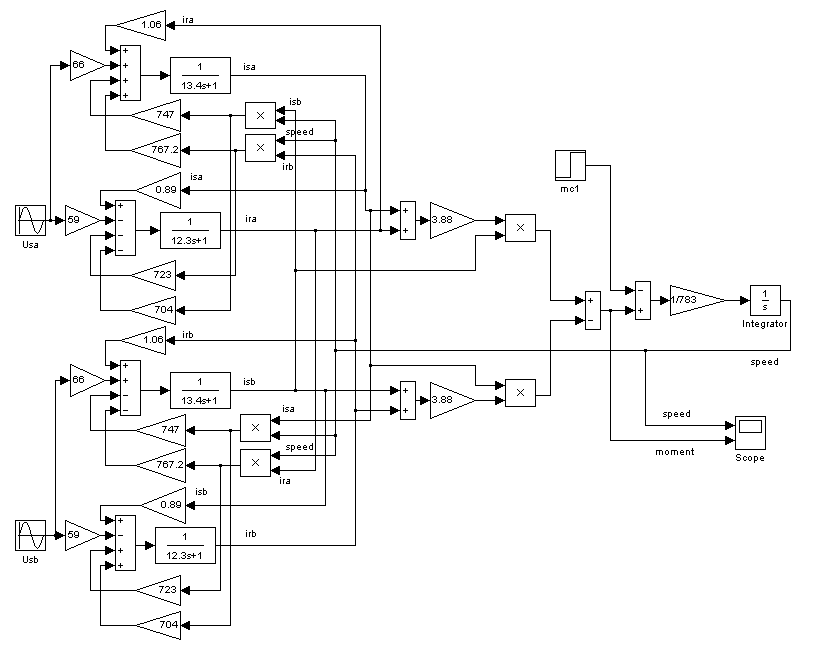
Модель АКЗ, построенная по уравнениям (1) – (6), представлена на рис. 1.
На вход модели в момент времени
![]() подаются напряжения
подаются напряжения
![]() ,
,
![]() ,
(
,
(![]() ),
тем самым реализуя прямой пуск.
),
тем самым реализуя прямой пуск.
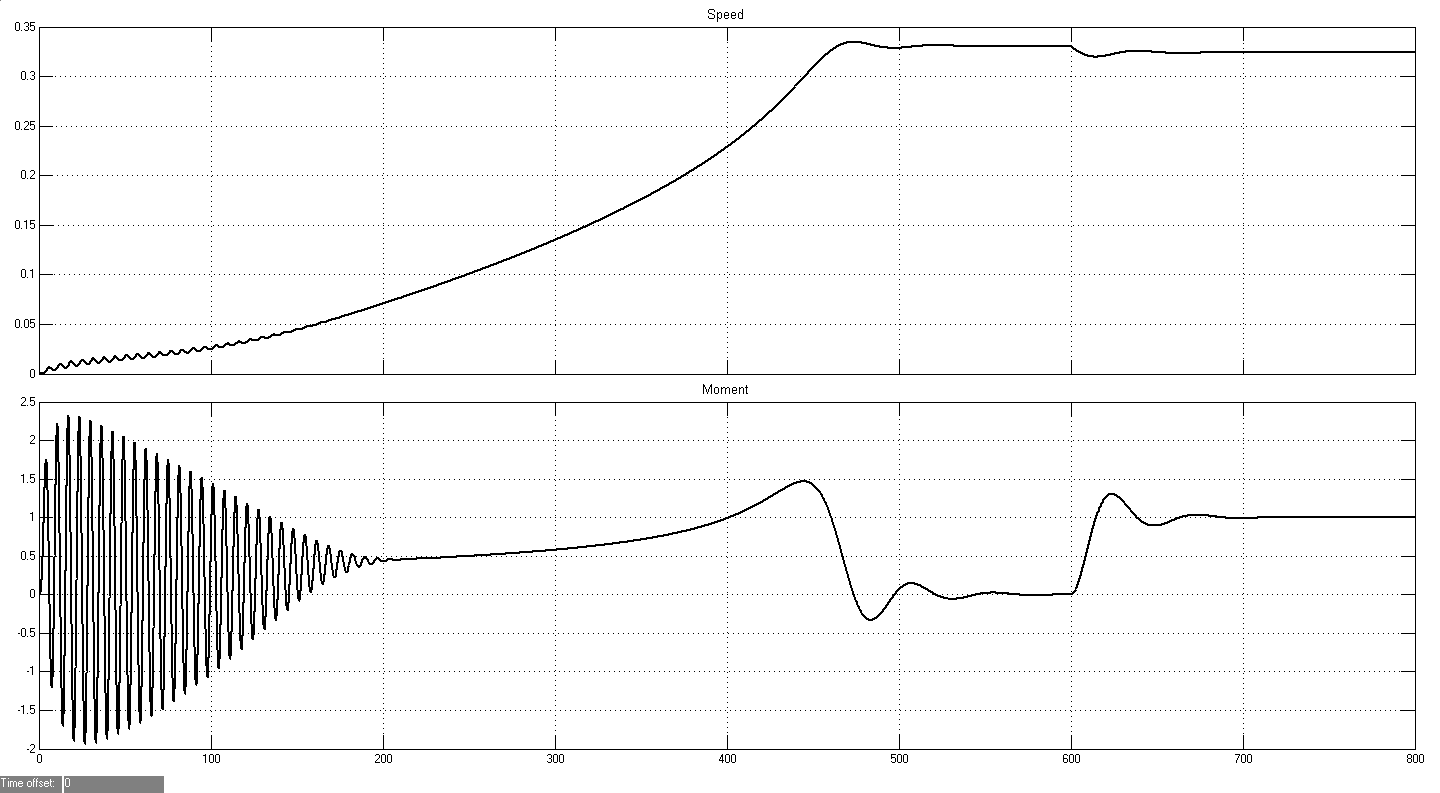
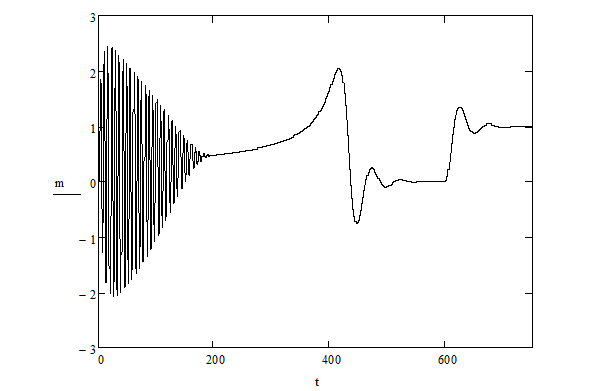
Осциллоскопы измеряют относительные значения электромагнитного момента и скорости. Результаты моделирования представлены на рис. 2.
Рис. 1. Модель АКЗ в неподвижной системе координат с переменными
![]()
Рис. 2. Результаты моделирования, относительные значения электромагнитного момента и скорости
- Проверку решения произведем в программном пакете «MathCAD 14».
-
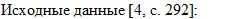
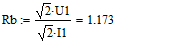
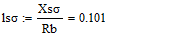
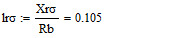
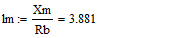
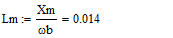
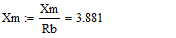
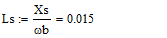
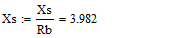
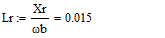
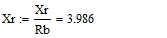




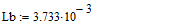







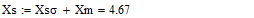
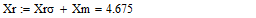
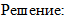
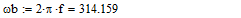
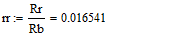
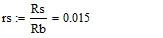
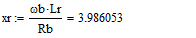
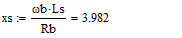
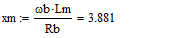
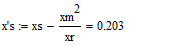
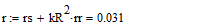
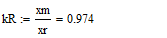
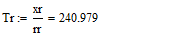
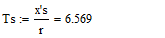
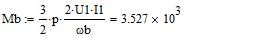
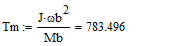
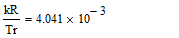



- Систему уравнений (**) преобразуем в систему однородных дифференциальных уравнений (ОДУ):
-
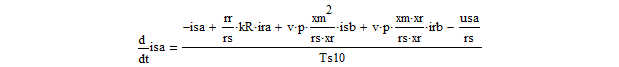

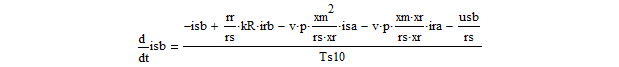
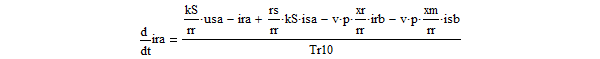
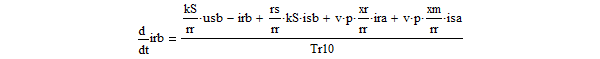
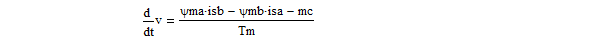
- Нелинейные уравнения оставим без изменения:
-


 В
систему ОДУ подставим значения потокосцеплений (ψma,
ψmb) и момента m.
В
систему ОДУ подставим значения потокосцеплений (ψma,
ψmb) и момента m.
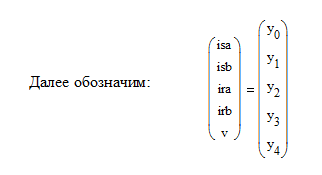
- Затем правые части ОДУ запишем в матричной форме, состоящей из 5 строк и одного столбца, в результате получим:
-
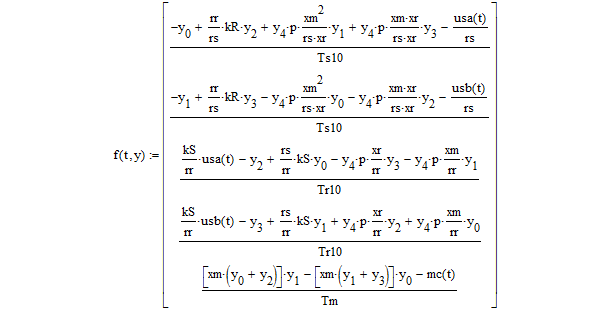
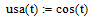

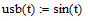 В
которой:
В
которой:
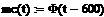
- Причем mc(t) – статический момент на валу двигателя.
- Зададим начальные условия isa(0) = 0, isb(0) = 0, v(0) = 0.
- Далее зададим функцию решения дифференциальных уравнений методом Рунге-Кутты четвертого порядка:
-
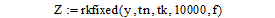
- где tn – время начала расчета;
- tk – время конца расчета;
- y – начальные условия;
- 10000 – количество рассчитываемых точек;
- f – функция, заданная матрицей, состоящей из правых частей ОДУ
- Чтобы вывести функцию f = m(t) зададим индекс n в пределах 0..10000 и получим:
-
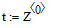
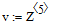

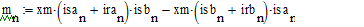
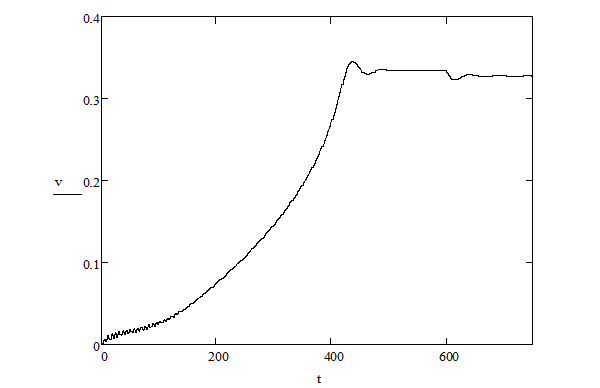
Результаты решения приведены на рис. 3 и 4.
Литература:
- Шрейнер Р.Т. Математическое моделирование электроприводов
- переменного тока с полупроводниковыми преобразователями частоты. Екатеринбург: УРО РАН, 2000. 654 с.
- Герман-Галкин С.Г. Компьютерное моделирование полупроводниковых систем Matlab 6.0: Учебное пособие. – Спб.: Корона принт. 2001. – 320с., ил.
-
Емельянов А.А., Клишин А.В., Медведев А.В. Математическая модель АД
в неподвижной системе координат с переменными
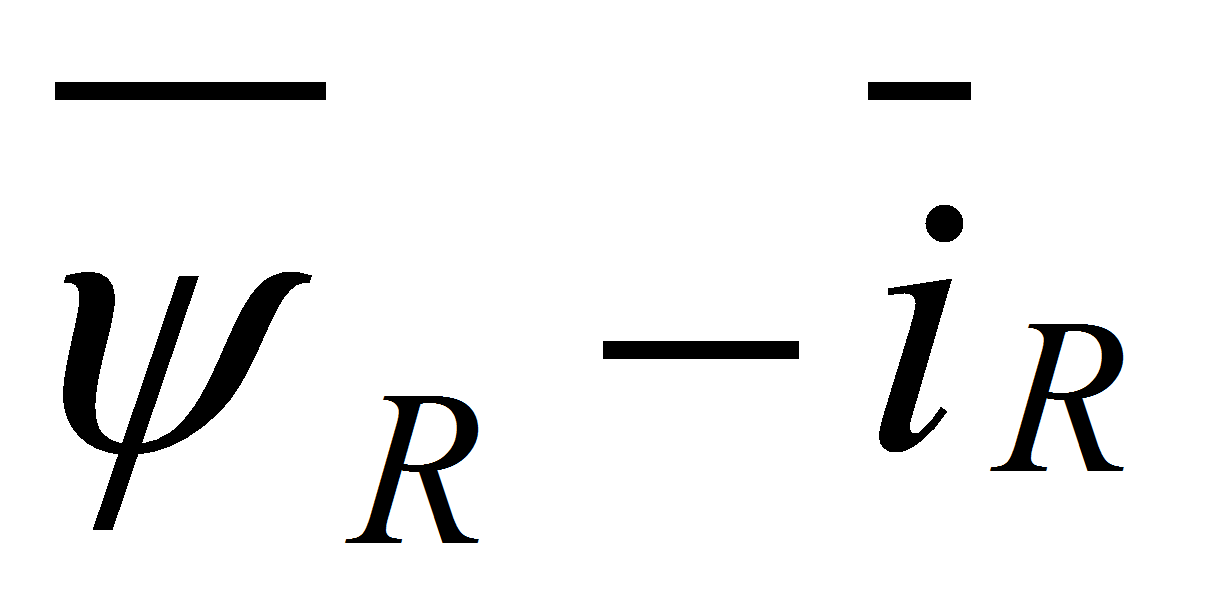 [Текст] / Молодой ученый. – 2010. -№4. – С.
8-24.
[Текст] / Молодой ученый. – 2010. -№4. – С.
8-24. - Шрейнер Р.Т. Электромеханические и тепловые режимы асинхронных двигателей в системах частотного управления. Екатеринбург: ГОУ ВПО «Рос. гос. проф.-пед. ун-т», 2008. 361 с.