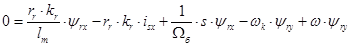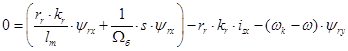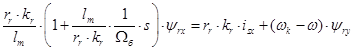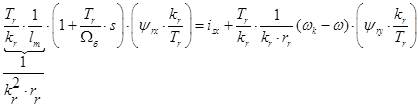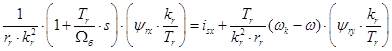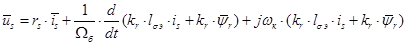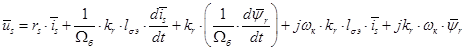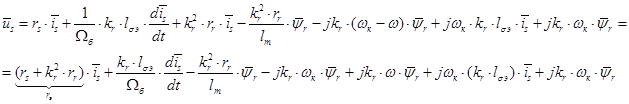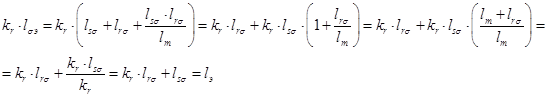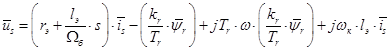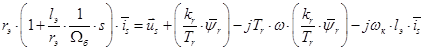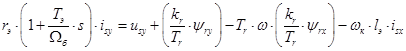Данная работа является продолжением опубликованной статьи [1], в которой были подробно показаны без сокращений способы и технологии получения пространственных векторов 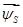 ,
, 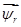 ,
, 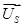 ,
, 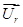 ,
, 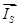 ,
, 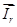 , в системе абсолютных единиц.
, в системе абсолютных единиц.
В работах [2; 3] приведено множество вариантов конечных результатов электромагнитного момента в зависимости от произведения проекций двух векторов (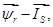
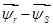 и т.д.). В этой статье сделан вывод одного из множества математических моделей асинхронного двигателя и сравнение полученных уравнений и структурной схемы с фундаментальной работой [3].
и т.д.). В этой статье сделан вывод одного из множества математических моделей асинхронного двигателя и сравнение полученных уравнений и структурной схемы с фундаментальной работой [3].
Итак, в работе [1] были получены основные уравнения асинхронного двигателя в произвольной системе координат 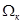 :
:
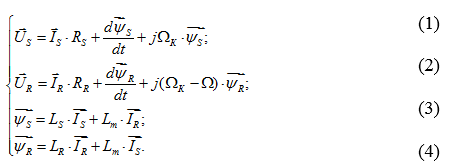
Переведем эти уравнения в систему относительных единиц.
В уравнениях (1) и (2) обе части разделим на 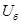 :
:
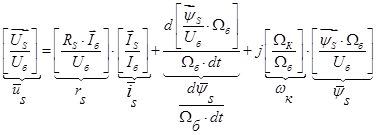
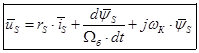 (5)
(5)
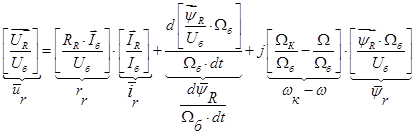
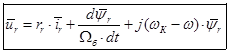 (6)
(6)
В уравнениях (3) и (4) обе части умножим на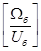 :
:
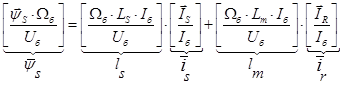
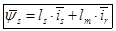 (7)
(7)
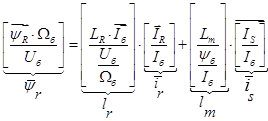
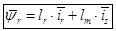 (8)
(8)
Итак, основные уравнения асинхронного двигателя с к. з. ротором (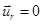 ) имеют следующий вид:
) имеют следующий вид:
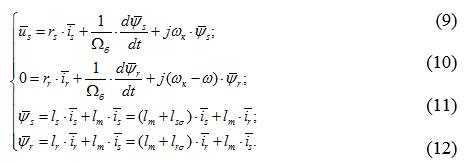
Электромагнитный момент определяется по формуле [2, c.131]:
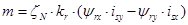 (13)
(13)
Уравнение движения:
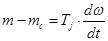 (14)
(14)
Так как электромагнитный момент определяется через переменные 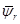 и
и 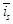 , то из уравнений исключим переменные
, то из уравнений исключим переменные 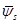 и
и 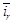 .
.
Из уравнения (12) выразим 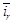 :
:
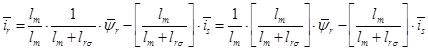
Обозначим 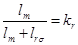 , тогда
, тогда
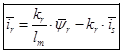 (15)
(15)
Из уравнения (11) исключим 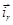 :
:
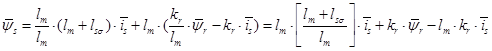
Обозначим 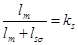 , тогда
, тогда
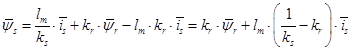
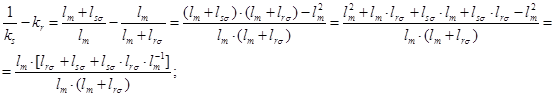
Обозначим 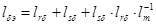 .
.
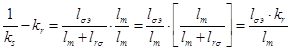
Тогда
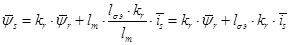
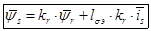 (16)
(16)
В уравнении (10) подставим 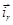 :
:
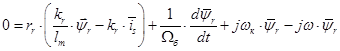 (17)
(17)
Отсюда выразим
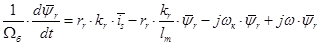 (18)
(18)
В уравнении (17) перейдем к оператору 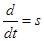 и разложим векторы
и разложим векторы 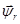 и
и 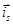 на проекции:
на проекции:
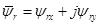
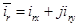
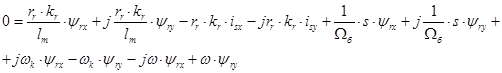 (*)
(*)
Проекция уравнения (*) на ось +1:
Проекция уравнения (*) на ось +j:
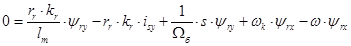 (20)
(20)
Из уравнения (20):
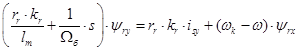
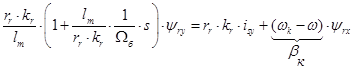
Разделим обе части полученного уравнения на (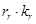 ):
):
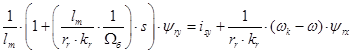
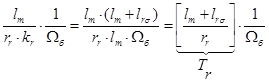
Тогда
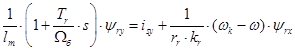
В соответствии с [3] перейдем к переменным 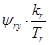 и
и 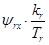
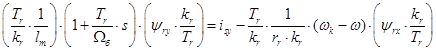
Выразим
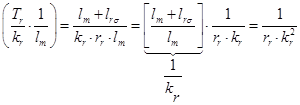
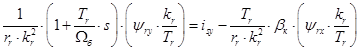
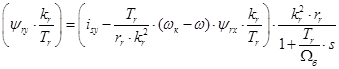 (21)
(21)
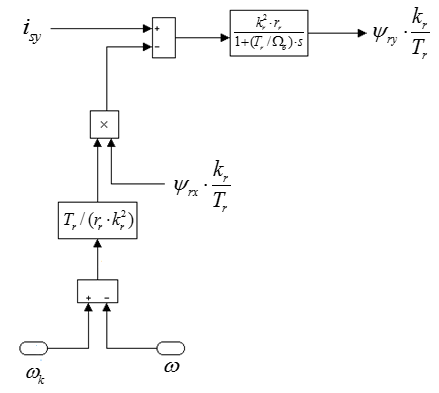
Рис. 1. Структурная схема для определения 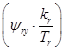 .
.
Аналогично для уравнения (19):
Разделим обе части уравнения на 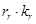 :
:
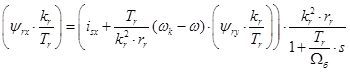 (22)
(22)
Полученному уравнению (22) соответствует следующая структурная схема:
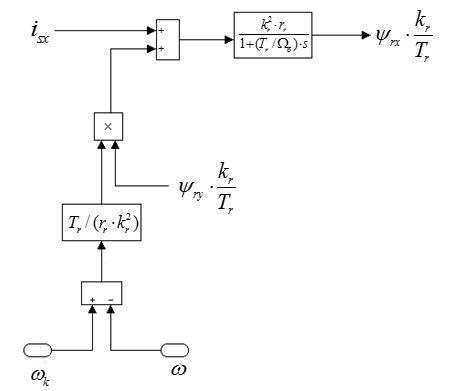
Рис. 2. Структурная схема для определения 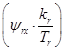 .
.
Из уравнения (9) исключим 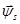 :
:
Подставим в это уравнение 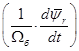 из уравнения (18):
из уравнения (18):
Обозначим 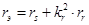 :
:
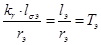
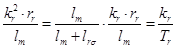 ,
,
где 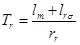
Переведем уравнения с 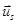 в изображениях, для этого выразим
в изображениях, для этого выразим 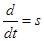
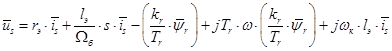
Выразим векторы 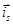 ,
, 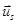 и
и 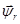 через проекции:
через проекции:
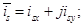
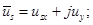
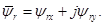
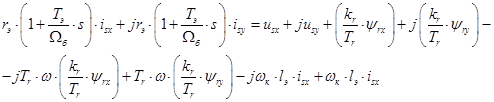 (**)
(**)
Проекция уравнения (**) на действительную ось +1:
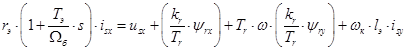 (23)
(23)
Проекция уравнения (**) на мнимую ось +j:
Из уравнения (17) выразим 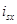 :
:
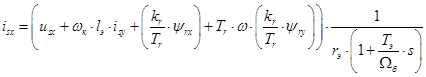
Структурная схема для реализации тока 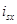 в MatLab-Simulink дана на рис. 3.
в MatLab-Simulink дана на рис. 3.
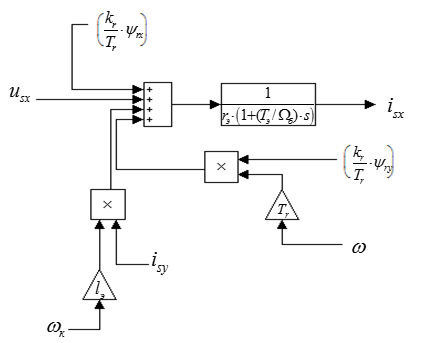
Рис. 3. Структурная схема проекции статорного тока 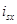 на ось +1.
на ось +1.
Аналогично из уравнения (24) выразим 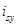 :
:
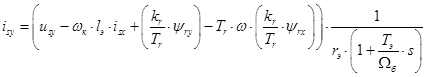
Структурная схема, соответствующая этому уравнению, представлена на рис. 4.
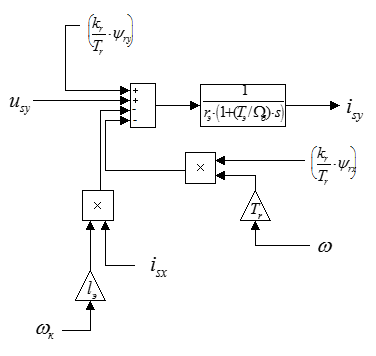
Рис. 4. Структурная схема проекции статорного тока 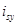 на ось +j.
на ось +j.
Структурная схема для реализации уравнения (13) дана на рис. 5:
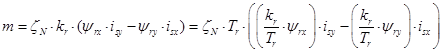
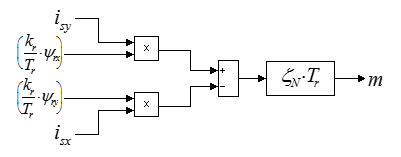
Рис. 5. Математическая модель электромагнитного момента m.
Наконец для уравнения (14):
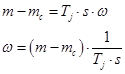
Структурная схема дана на рис. 6.
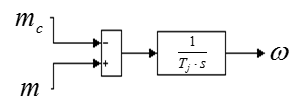
Рис. 6. Математическая модель уравнения движения.
На рис. 7. Представлены субблоки из математической модели АД, преобразователя координат и блока ориентации.
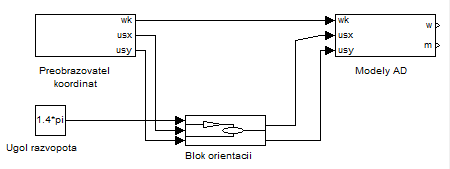
Рис. 7. Система из математической модели двигателя, преобразователя координат и блока ориентации.
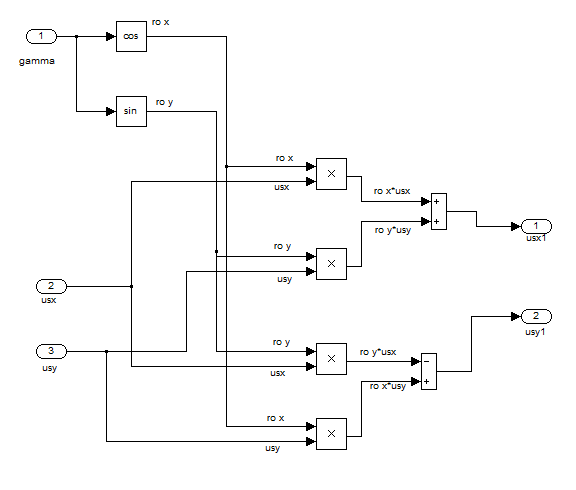
Рис. 8. Блок ориентации.
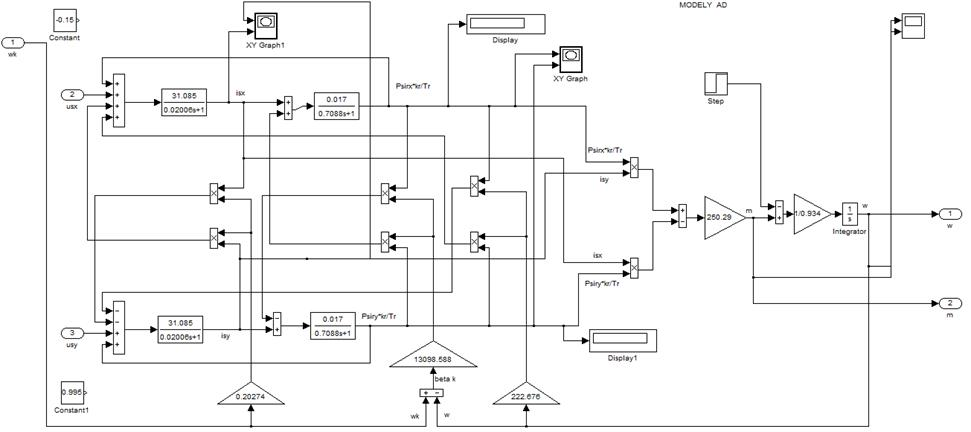
Рис. 9. Модель асинхронного двигателя.
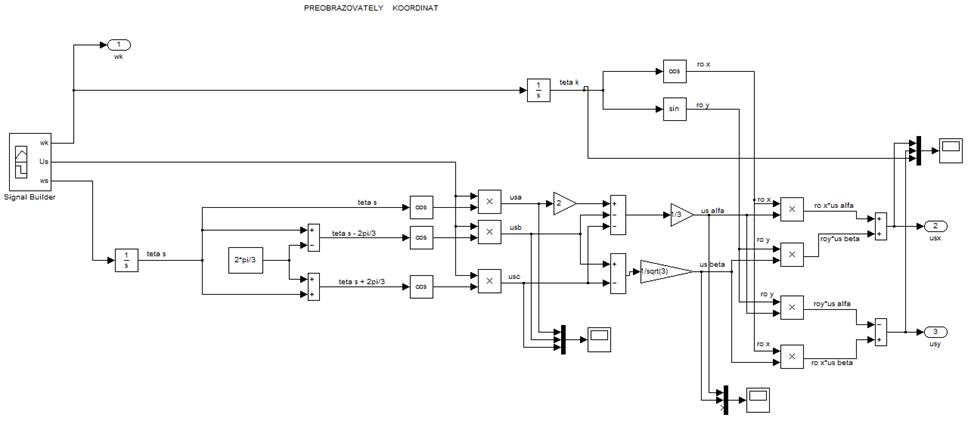
Рис. 10. Преобразователь координат.
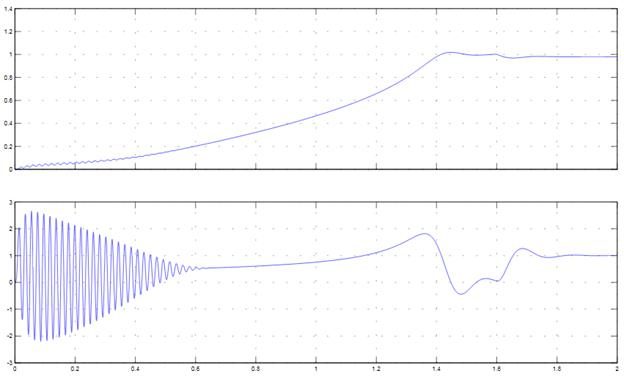
Рис. 11. Графики скорости и момента
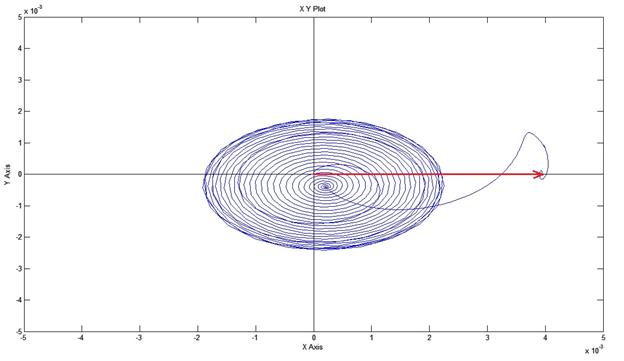
Рис. 12. Ориентация системы координат по потокосцеплению ротора
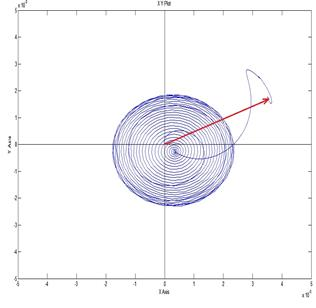
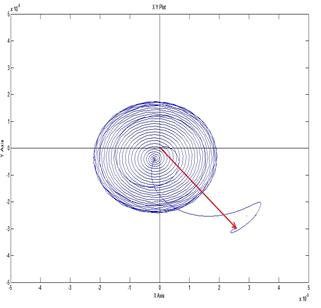
Рис. 13. Произвольная ориентация системы координат
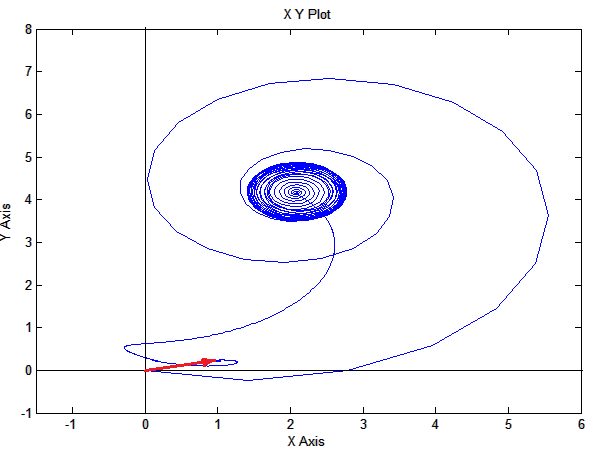
Рис. 13. Годограф изменения статорного тока 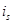 при пуске.
при пуске.
Литература:
1. Пространственные векторы в асинхронном двигателе в относительной системе единиц// Молодой ученый. — 2015. — №11. — С. 133-156.
2. Шрейнер Р. Т. Электромеханические и тепловые режимы асинхронных двигателей в системах частотного управления [Текст]: учеб. пособие / Р. Т. Шрейнер, А. В. Костылев, В. К. Кривовяз, С. И. Шилин. Под ред. проф. д.т.н. Р.Т.Шрейнера. Екатеринбург: ГОУ ВПО «Рос. гос. проф.-пед. ун-т»., 2008. 361 с.
3. Шрейнер Р. Т. Математическое моделирование электроприводов переменного тока с полупроводниковыми преобразователями частоты Екатеринбург УРО РАН, 2000. 654 с.
4. Математическая модель АД в неподвижной системе координат c переменными / А. А. Емельянов [и др.] // Молодой ученый. — 2010. — №3. Т.1. — С. 8-23.