В статье рассматриваются результаты исследования электромагнитного вибровозбудителя с последовательно включенным конденсатором в электрическую цепь, состоящей из механической и электрической подсистем. Показано, что с помощью уравнения Лагранжа — Максвелла может быть осуществлена взаимосвязь между механической и электрической подсистемами. Выведены соотношения, описывающие процессы установления амплитуд и фаз колебаний как в механической, так и в электрической подсистемах. Приведены уравнения, связывающие выход (размах) колебаний вибровозбудителя с его входом (напряжением) сети. В результате представлены формулы, позволяющие производить корректировки при решении системы, описывающей работу электромагнитного вибровозбудителя в двухтактном режиме.

Исследуемая система содержит две подсистемы: механическую и электрическую, причем каждая из них является сама по себе полной колебательной подсистемой. Поэтому в уравнениях Лагранжа-Максвелла описываются взаимосвязанные механические и электромагнитные процессы [1] исследуемого вибровозбудителя (1)

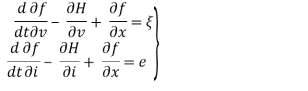(1)

Функция Лагранжа f содержит все составляющие функции

,

где

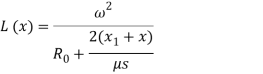(2)

В диспутативной функции Релея отражены , а внешней механической силы нет,

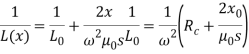
Таким образом, исследуемыми уравнениями являются следующие:

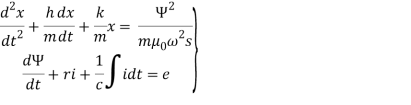(3)

Указанная выше система уравнений ранее имела вид (2). Однако исследование было проведено искусственно. Второе уравнение системы (2) решено отдельно, рассматривали его как параметрическое. Для этого кривая вышеуказанной зависимости индуктивности аппроксимирована специально подобранной экспоненциальной функцией, удобной только для дальнейшего интегрирования [2].

Второе уравнение (3) приводим к одной переменной с помощью , где L заменим зависимостью (2). Тогда систему (3) запишем в виде:

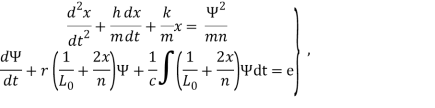(4)

где

Выведем соотношения, с помощью которых описываются процессы установления амплитуд и фаз колебаний как в механической, так и в электрической подсистемах и их установившиеся значения. Для этого вводим следующую замену переменных:

(5)

(6)

Продифференцировав правые стороны выражений (5) и (6), имеем:

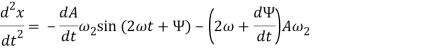(7)

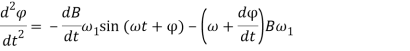(8)

Подставив (5) — (6) в систему уравнений (4), получим вместо уравнений для мгновенных величин систему уравнений для параметров амплитуды и фазы в общем случае как функции времени, причем эти уравнения будут представлены в таком виде, который позволяет исследовать процесс установления ранних параметров. После подстановки имеем следующие уравнения:

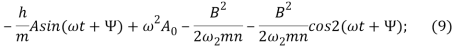
(10)

Продифференцировав правые выражения (5) и (6) и сравнивая их с соответствующими (9) и (10) выражениями, получим следующие равенства:

Совместное решение каждой пары уравнений (9), (11) и (10), (12) дает следующие соотношения для производных амплитуд и фаз:

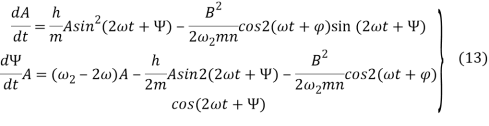
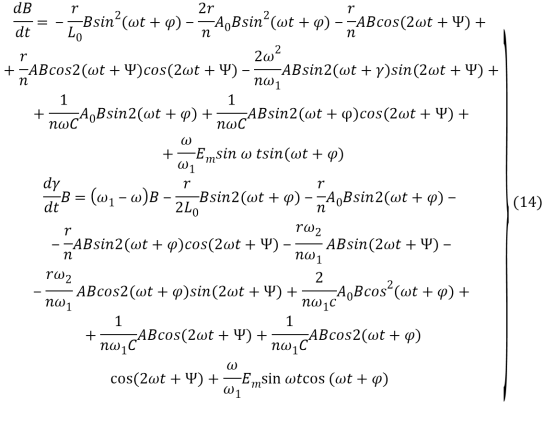
Кроме того, из уравнения (14) получаем следующее равенство для определения постоянной составляющей механического перемещения:

(15)

В первом приближении, усреднив правые части уравнений (13) и (14) за период Т, считая при этом параметры колебаний неизменными, запишем следующие уравнения:

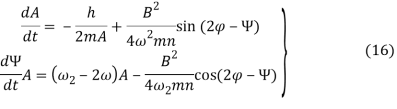
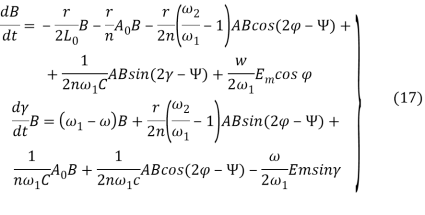
В установившемся режиме из системы уравнений (16) получим

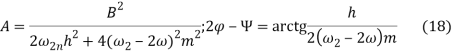
В этом же режиме систему уравнений (17) можно привести к виду

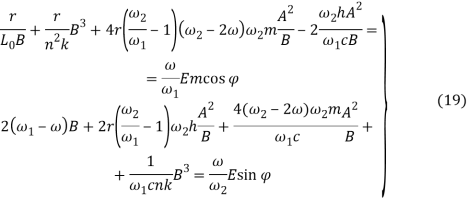
или к следующему относительно В бикубическому уравнению

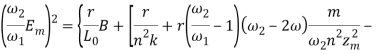
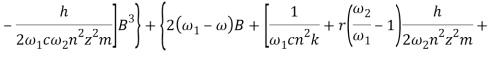
Упростив запись уравнения (20) и введя обозначения

,

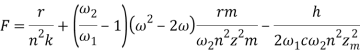
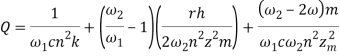получим

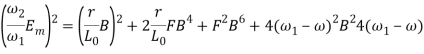
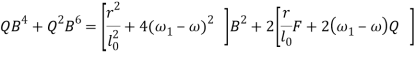
Теперь с помощью (18) заменим в уравнении (21) В на А

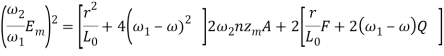
(22)

Наконец, одним уравнением напрямую свяжем выход — размах колебаний вибровозбудителя с его входом — напряжением сети.

С помощью уравнения (22) можно построить любые резонансные кривые при всевозможных заданных в нем параметрах [3]. В исследуемом объекте — вибровозбудителе имеются две колебательные подсистемы, поэтому возможны резонансы на двух частотах. Следовательно, по аналогии с двухконтурной радиотехнической системой здесь тоже можно ожидать два простых частных резонанса и один сложный резонанс.

После рассмотрения электромагнитного вибровозбудителя в однотактном варианте, возбуждаемой удвоенной частотой напряжения питания, перейдем к анализу использования вибровозбудителя с последовательно включенным конденсатором в двухтактном варианте. Питание двух обмоток возбуждения осуществляется напряжениями, сдвинутыми по фазе на .

Приведенные источники э. д.с. вызовут в идентичных обмотках также сдвинутые токи, а потоки — квадраты потоков, которые будут сдвинуты уже на Т и будут действовать в разных обмотках, оказывая воздействие на якорь попеременно, что равносильно воздействию на него одной общей силы частотой 2 с амплитудой, в два раза большей, чем в однотактном случае, причем эта сила не содержит постоянной составляющей. Учитывая эти изменения, можно внести в вышеполученные результаты в квадратных скобках правой части уравнения (22) следующие коррективы:

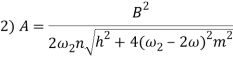
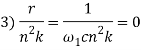
Таким образом, в результате исследования электромагнитного вибровозбудителя с последовательно соединенным конденсатором в электрическую цепь представлены формулы, позволяющие производить корректировки при получении решения системы, описывающей работу электромагнитного вибровозбудителя в двухтактном режиме.

Литература:

1. Демирчян К. С., Нейман Л. Р., Коровкин Н. В., Чечурин В. Л. Теоретические основы электротехники. Учебник для вузов. Том 1. СПб.: Питер, 2003.-463 с.
2. Ту.Ю. Современная теория управления. -М.; Машиностроение, 1971. -300 с.
3. John Bird. “Electrical and Electronic Principles and Technology” LONDON AND NEW YORK, 2014.-455 p.