В статье авторы пишут о малоизученных и малоизвестных математических операциях.
Ключевые слова : математика, операции, действия, малоизученность, факториалы, супремум, инфимум, сигнум, значение, определение.
В математике существуют различные действия — операции. По определению, операция в математике — это преобразование одного объекта в другой, которое ставит в соответствие одному или нескольким элементам множества (аргументам) другой элемент (значение). Например, сложение. Это операция. Или вычитание, умножение, деление, возведение в степень, извлечение корня из числа, логарифм, факториал, синус, косинус, тангенс, котангенс, интеграл, дифференциал — это известные математические операции, о которых знает очень большой процент населения, в особенности математики и учёные.
Но ведь существуют и другие операции, которые менее известны. Например, есть так называемая операция, которая обозначается как sgn, а называется сигнум.
Сигнум — это кусочно-постоянная функция действительного аргумента. По сути, операция очень лёгкая и весьма узконаправленная. Функция эта имеет значение -1, +1, 0. Зависит это от того, какой знак будет у данного действительного числа. Записать нахождение sgn x мы можем следующим образом:
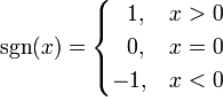
Рис. 1. Определение сигнума числа х
«Сигнум от x — функция от действительного числа x, равная 1 для положительных x, равная нулю при x = 0 и равная –1 для отрицательных x» — пишет О. А. Старова в своей научной статье «Кусочно-заданные функции». [1, с 26]
Практическое значение сигнума: сигнум применяется в теории обработки сигналов, в математической статистике и других разделах математики, где нужна компактная запись для индикации знака числа.
Помимо известного всем факториала и субфакториала, существуют ещё восемь видов факториалов. Рассмотрим некоторые самые интересные из них.
Например, праймориал . Праймориал числа n — это произведение всех простых чисел от одного до числа n.
Праймориал обозначается символом #. Например, 7# = 2*3*5*7 = 210. То есть мы просто перемножаем все простые числа до числа 7.
«Праймориал числа — это произведение всех простых множителей, не превышающих данное число. Обозначается он n#. Например, 10# = 7 ∙ 5 ∙ 3 ∙ 2». — пишет О. В. Панишева в статье «Расширение понятия об арифметических операциях над числами в школьном курсе математики». [2, с 69]
Возрастание функции праймориала можно наглядно продемонстрировать следующим графиком:
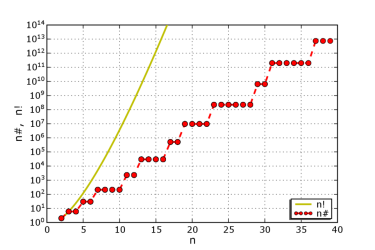
Рис. 2. График обычного Факториала и график Праймориала
Ещё один вид факториала — Фиббоначиал . Назван по числам Фибоначчи. Фиббоначиал числа n — это произведение всех чисел Фибоначчи, кроме 0 до числа n. Обозначается как n!F.
Например, 10!F = 1*1*2*3*5*8 = 240. Как любой другой факториал, возвести в него можно только натуральное число.
Факториал под названием «Фиббоначиал» используется в математике для определения биномиальных коэффициентов Фибоначчи.
Ещё один из видов — суперфакториал , который бывает в двух вариациях — Суперфакториал Слоуна и Суперфакториал Пиковера.
«Существуют и другие виды факториалов, найти информацию о которых можно предложить самим обучающимся — это гиперфакториал, суперфакториал Слоуна, Пиковера, Фибоначчиал». — пишет О. В. Панишева [2, с 72]
Из-за сложности Суперфакториала Пиковера рассмотрим только Суперфакториал Слоуна.
Суперфакториал Слоуна числа n — это произведение факториалов чисел от одного до числа n. Обозначается как sf(n).
Например, возьмём число 4. Sf (4) = 1! * 2! * 3! * 4! = 1 * 2 * 2 * 3 * 2 * 3 * 4 = 288. Это весьма быстрорастущая функция.
Суперфакториал Слоуна используется для вычисления произведения факториалов чисел, меньших или равных заданному.

Рис. 3. Суперфакториал Слоуна, основные сведения
Гиперфакториал — ещё один из видов факториала. Гиперфакториал числа n — это произведение всех целых чисел от 1 до n, возведённое в степень, равную этому же числу.
Например, есть число 3. Гиперфакториал будет высчитываться следующим образом: H(3) = 1 * 2 * 2 * 3 * 3 * 3 = 108.
Гиперфакториал используется в математике для описания определённого роста числовых последовательностей.
Также существует ещё и малоизвестный обратный факториал . По определению, обратный факториал — это число, факториал которого n! и есть исходное число. Обозначается как n!? или n?
Например, мы знаем, что 5! = 120.
Тогда 120? = 5.
24? = 4.
Обратный факториал используется для решения задач комбинаторики. Он позволяет найти число, факториал которого равен исходному числу (n!). В частности, n!? — это число предметов, количество перестановок которых (способов расположения) равно n!
На этом остановимся с малоизвестными факториалами. Перейдём к другим малоизвестным операциям. Все знают про логарифм. Но далеко не все люди знают, что есть операция, обратная логарифмированию, которая называется потенцирование . По-другому её ещё называют антилогарифм . Антилогарифм — это число, логарифм которого равен заданному значению.
Обозначается как antilog. Например, есть выражение antilog10 3. Если логарифм из 1000 по основанию 10 равен 3, то соответственно антилогарифм из трёх по основанию десять будет = 1000.
То есть antilog10 3 = 1000.
«Для того, чтобы по какому-нибудь логарифму найти число соответствующее, мы обращаемся к антилогарифмам» — пишет Б. В. Гопфен в книге «Логарифмы, Антилогарифмы и Тригонометрические величины в упрощенных таблицах». [3, с 14]
Антилогарифмы используются в различных областях. Например:
В химии — для расчёта pH растворов;
В физике — для описания процессов затухания колебаний;
В экономике — для моделирования роста населения или капитала.

Рис. 4. Таблица Антилогарифмов
Последние действия, что мы рассмотрим, это супремумы и инфимумы, тоже очень малоизвестные, но очень значимые операции.
По определению, супремум множества X — это наименьший элемент множества, который больше или равен любому элементу множества X. Супремум обозначается как sup X.
«Пусть числовое множество M ограничено сверху. Наименьшая из всех верхних граней данного множества называется точной верхней гранью или супремумом этого множества и обозначается sup M или sup x∈M x (от латинского слова “supremum” — наибольший)». — объясняется в учебнике «Математический анализ. Часть 1» [4, с 56]
Объясню проще. Например, есть множество Х= {2;3;4;5;6}. Оно является подмножеством, то есть входит в множество натуральных чисел N. Супремумом множества Х будет 6, наименьшее из натуральных чисел N, большее любого элемента множества Х.
Записываться будет так: sup X = 6.
Инфимум, абсолютно наоборот: инфимумом подмножества X частично упорядоченного множества (или класса) M называется такой наибольший элемент множества M, который равен или меньше всех элементов множества X. Обозначение: inf X.
«Пусть числовое множество M ограничено снизу. Наибольшая из всех нижних граней данного множества называется точной нижней гранью или инфимумом этого множества и обозначается: inf M, или inf x∈M x (от латинского “textitinfimum” — наименьший)» — подтверждается в учебнике «Математический анализ. Часть 1» [4, с 56]
Например, есть множество X= {4;5;6;7;8;9}. Оно входит в множество натуральных чисел N. Инфимумом будет число 4, так как это наибольшее из натуральных чисел, меньшее любого элемента из X.
Записываться будет так: inf X = 4.
Супремум и инфимум нужны для описания границ множеств в математике.
Эти понятия помогают:
– Понимать поведение функций и последовательностей, особенно когда они не сходятся в традиционном смысле;
– Решать задачи, связанные с пределами, непрерывностью и оптимизацией;
– Описывать границы и пределы в различных областях, включая исчисление, реальный анализ, проблемы оптимизации и экономическую теорию.
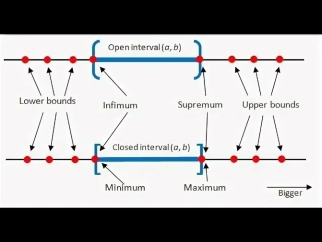
Рис. 5. Супремум и инфимум на координатной прямой
Вывод. В математике существуют многие малоизученные операции, о которых практически никто не знает. Но забывать о них не следует: у каждой операции в математике есть своё значение, смысл и предназначение. Каждая операция может помочь для решения определённых задач в разных сферах.
Литература:
- О. А. Старова. Кусочно-заданные функции. Журнал: «Математика. Всё для учителя». Выпуск № 3 (51), март 2015.
- О. В. Панишева. Инновационные подходы к обучению математике в школе и в Вузе. Материалы IV Всероссийской научно-практической конференции (Омск, 15 марта 2024 года). Статья: «Расширение понятия об арифметических операциях над числами в школьном курсе математики». Омск. Издательство ОмГПУ. 2024 г. — 223 с.
- Б. В. Гопфен. Логарифмы, Антилогарифмы и Тригонометрические величины в упрощенных таблицах. Москва. 14-я типография Моск. Гор. Сов. Нар. Хоз. (Бывшая городская). 2-ое издание. 1920 г. — 16 с.
- Н. В. Зайцева, Э. Л. Шишкина. «Математический анализ. Часть 1». Учебник для Вузов. Москва. МГУ. Издательство Московского университета. 2024. — 328 с.

