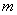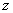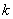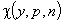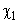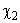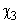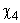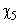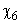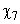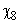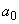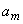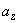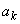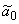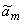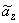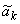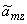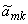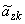Приводится практическая реализация методов планирования эксперимента при составлении аппроксимационной модели функций многих переменных.
Ключевые слова:имитаторы динамики полета, аэродинамические коэффициенты функции многих переменных, аппроксимационные модели, методы планирования эксперимента.
При разработке авиационных тренажеров используется таблично-графическое представление функций многих переменных, в частности, аэродинамических коэффициентов [1…4]. Для уплотнения данных можно воспользоваться аппроксимационными моделями. Ниже приводится один из возможных методов аппроксимации с использованием методов планирования эксперимента [5].
Рассмотрим функцию 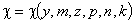 . В результате анализа представленной информации удалось выявить переменные
. В результате анализа представленной информации удалось выявить переменные 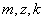 , принимающие только два значения (нижний и верхний уровни; используются индексы «н» и «в» соответственно).
, принимающие только два значения (нижний и верхний уровни; используются индексы «н» и «в» соответственно).
Введем
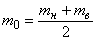 ,
, 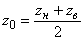 ,
, 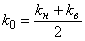 ;
;
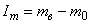 ,
, 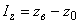 ,
, 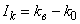 ;
;
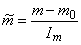 ,
, 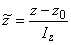 ,
, 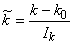 .
.
Предполагается:
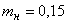 ,
, 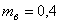 ;
; 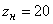 ,
, 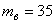 ;
; 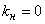 ,
, 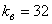 ;
;
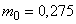 ,
, 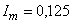 ;
; 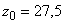 ,
, 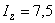 ;
;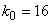 ,
, 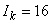 .
.
Кодированные значения нижних и верхних уровней переменных будут равны 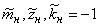 ,
, 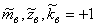 , а для центра эксперимента —
, а для центра эксперимента — 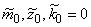 .
.
Будем искать аппроксимационную модель в виде
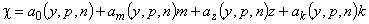 .
.
Воспользуемся ортогональной матрицей планирования (вид в натуральных переменных — табл.1). Следствием ротатабельности матрицы является равная точность линейной модели во всех направлениях относительно центра (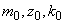 ).
).
Таблица 1
Матрица планирования
|
№ опыта |
|
|
|
|
|
1 |
0,15 |
20 |
0 |
|
|
2 |
0,4 |
20 |
0 |
|
|
3 |
0,15 |
35 |
0 |
|
|
4 |
0,4 |
35 |
0 |
|
|
5 |
0,15 |
20 |
32 |
|
|
6 |
0,4 |
20 |
32 |
|
|
7 |
0,15 |
35 |
32 |
|
|
8 |
0,4 |
35 |
32 |
|
В кодированных переменных получим модель вида
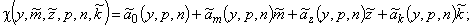
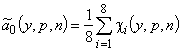 ,
,
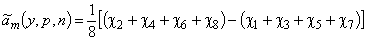 ,
,
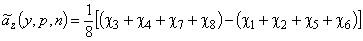 ,
,
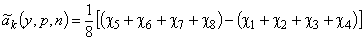
Переходя к натуральным переменным, получим
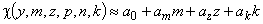 ;
;
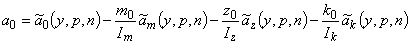 ,
,
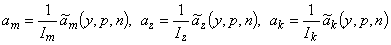 .
.
При фиксированных значениях p и n коэффициенты модели будут функциями одной переменной y (табл. 2).
Таблица 2
Значения коэффициентов при p=40 и n=20.
|
y |
0,5 |
0,7 |
1,0 |
1,1 |
|
|
0,0697 |
0,0620 |
0,0543 |
0,0354 |
|
|
0,0100 |
0,00650 |
0,0110 |
0,0380 |
|
|
-0,00063 |
-0,00036 |
0,00025 |
0,0013 |
|
|
0,00033 |
0,000707 |
0,00128 |
0,00136 |
В дальнейшем после аппроксимации коэффициентов 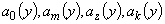 полиномами Лагранжа была получена модель
полиномами Лагранжа была получена модель
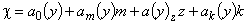 ,
,
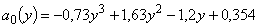 ,
,
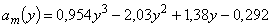 ,
,
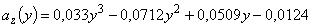 ,
,
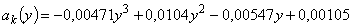 .
.
Если полученные модели в выбранных интервалах варьирования факторов окажутся не адекватными, то возможны их уточнения с учетом эффектов взаимодействия (табл.3):
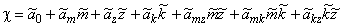 .
.
Таблица 3
Значения коэффициентов при p=25 и n=20.
|
y |
0,3 |
0,5 |
0,8 |
1,0 |
|
|
0,0368 |
0,0392 |
0,0570 |
0,0840 |
|
|
0,00025 |
-0,00025 |
-0,0015 |
0,0010 |
|
|
-0,00425 |
-0,00325 |
-0,0025 |
0,0015 |
|
|
0,00225 |
0,00575 |
0,0125 |
0,0170 |
|
|
0,00225 |
0,00225 |
0,00175 |
0,0065 |
|
|
0,00075 |
0,00025 |
0,00025 |
0 |
|
|
0,00025 |
0,00025 |
0 |
0,0005 |
Таким образом, для фиксированных значений p и n по матрицам планирования будет осуществлена аппроксимация функции 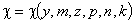 , как функции четырех переменных.
, как функции четырех переменных.
Если используются полиномы Лагранжа второго порядка, то аппроксимационные модели для случая p=0, n=20 имеют вид:
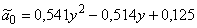 ,
,
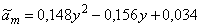 ,
,
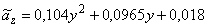 ,
,
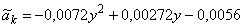 ,
,
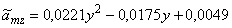 ,
,
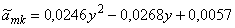 ,
,
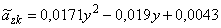 .
.
Приведенная методика эффективно использовалась для подготовки баз данных имитаторов динамики полета (уточнение на каждом шаге интегрирования начальных условий задачи Коши при решении уравнений динамики полета методом Рунге-Кутта).
Литература:
1. Andreev A. N., Danilov A. M., Klyuev B. V., Lapshin E. V., Blinov A. V., Yurkov N. K. Information models for designing conceptual broad-profile flight simulators / Measurement Techniques. August 2000. — Vol.43. Issue 8. — P.667–672.
2. Гарькина И. А., Данилов А. М., Иващенко Н. Ю. Аппроксимация таблично-графически заданных функций: модели аэродинамических коэффициентов / Московское научное обозрение. –№ 3(31). –2013. — С.9–18.
3. Данилов А. М., Гарькина И. А., Домке Э. Р. Математическое и компьютерное моделирование сложных систем. — Пенза: ПГУАС, 2011. -296 с.
4. Будылина Е. А., Гарькина И. А., Данилов А. М., Сухов Я. И. Некоторые подходы к анализу и синтезу сложных систем / Молодой ученый. — № 10(57). — 2013. — С.105–107.
5. Гарькина И. А., Данилов А. М. Прошин А. П., Соколова Ю. А. Планирование эксперимента. Обработка опытных данных: монография. Под ред. проф. А. М. Данилова. — М.: Палеотип. — 2005. — 272 с.