Для оценки качества пилотажных свойств транспортных самолетов, описываемых в виде
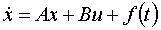
предлагается использовать прошедший практическую апробацию функционал вида [1…4]
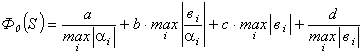 ,
,
где 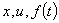 — соответственно векторы фазовых координат управляющих и возмущающих воздействий;
— соответственно векторы фазовых координат управляющих и возмущающих воздействий; 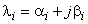 — собственные числа матрицы А;
— собственные числа матрицы А; 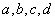 — весовые константы. Для продольного движения после определения весовых констант с использованием экспериментальных данных его можно представить в виде:
— весовые константы. Для продольного движения после определения весовых констант с использованием экспериментальных данных его можно представить в виде:
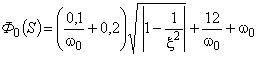 ,
,
где 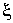 — безразмерный коэффициент затухания;
— безразмерный коэффициент затухания; 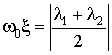 .
.
Для колебательных систем 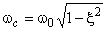 совпадает с собственной частотой. Для апериодических систем
совпадает с собственной частотой. Для апериодических систем 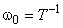 . При этом характеристическое уравнение имеет вид
. При этом характеристическое уравнение имеет вид
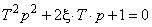 .
.
Определение областей 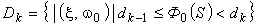 равных оценок пилотажных свойств производилось с учетом оценок по десятибалльной шкале Купера-Харпера (рис.1; сплошные линии — оценки, полученные по предложенному функционалу, пунктир — области, полученные экспериментально по шкале Купера-Харпера). Избирательность рассматриваемого функционала для определения классов ЛА к сожалению недостаточна (для класса 3,5 значение
равных оценок пилотажных свойств производилось с учетом оценок по десятибалльной шкале Купера-Харпера (рис.1; сплошные линии — оценки, полученные по предложенному функционалу, пунктир — области, полученные экспериментально по шкале Купера-Харпера). Избирательность рассматриваемого функционала для определения классов ЛА к сожалению недостаточна (для класса 3,5 значение 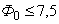 ; для класса
; для класса 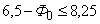 ). Поэтому наравне с использованием
). Поэтому наравне с использованием 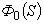 для оценки ЛА предлагается использовать в качестве частных критериев сами значения
для оценки ЛА предлагается использовать в качестве частных критериев сами значения 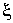 и
и 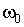 .
.
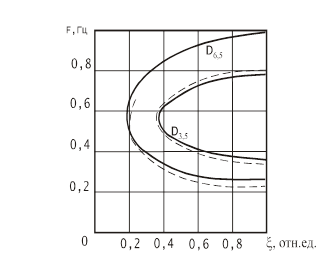
Рис.1. Области равных оценок пилотажных характеристик
Для колебательной системы
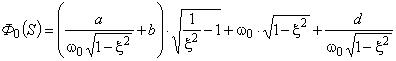 ,
,
или
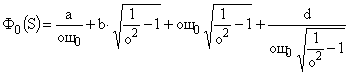 .
.
Введя традиционно используемые характеристики управления
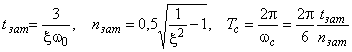 (
(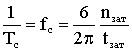 ),
),
получим:
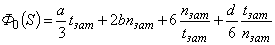 ,
,
или
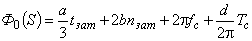 ,
,
или
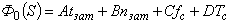 .
.
При принятых значениях весовых констант (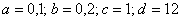 )
)
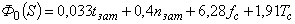 .
.
В частности 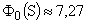 при
при 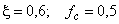
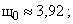
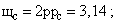
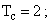
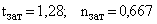 . Для сравнения:
. Для сравнения: 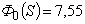 при
при 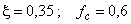
(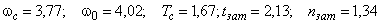 ).
).
При фиксированном 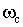 с ростом
с ростом 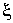 значение
значение 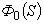 убывает:
убывает:
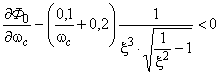
(пилоты-эксперты стремятся увеличить 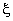 при работе на тренажере).
при работе на тренажере).
С ростом 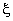 значение
значение 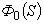 уменьшается, класс системы улучшается (рис.2).
уменьшается, класс системы улучшается (рис.2).
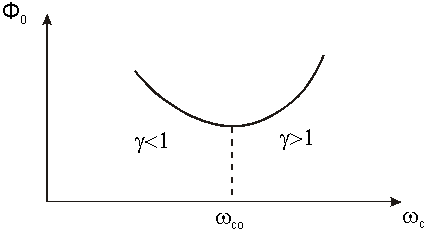
Рис. 2. Функционал качества
При 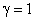
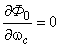 .
.
При этом при 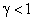
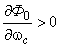 , при
, при 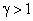
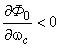 ,
,
то есть при 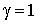 и
и 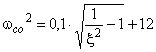 , или
, или 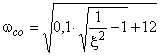
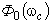 достигает минимума.
достигает минимума.
Для уменьшения 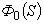 (или для улучшения класса системы) при фиксированном
(или для улучшения класса системы) при фиксированном 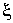 сначала надо вычислить
сначала надо вычислить 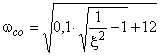 ,затем сравнить
,затем сравнить 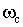 со значением
со значением 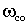 :
:
если 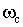 <
< 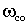 , то надо двигаться в сторону увеличения
, то надо двигаться в сторону увеличения 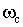 до значения
до значения 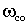 , если же
, если же 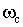 >
>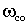 , то надо двигаться в сторону уменьшения
, то надо двигаться в сторону уменьшения 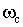 до
до 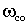 (рис. 2). Например, пусть
(рис. 2). Например, пусть 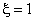 . Рассмотрим
. Рассмотрим 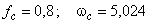 . При этом
. При этом 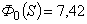 . Здесь
. Здесь 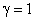 при
при 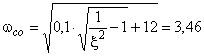 .
.
Как видим, 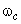 >
>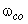 и надо двигаться в сторону уменьшения
и надо двигаться в сторону уменьшения 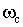 . Наименьшее значение
. Наименьшее значение 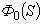 будет при
будет при 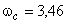 . При этом
. При этом 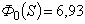 .Дальнейшее уменьшение частоты привело бы уже к увеличению
.Дальнейшее уменьшение частоты привело бы уже к увеличению 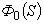 . Например,
. Например, 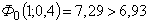 . Для этого значения
. Для этого значения 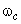 имели бы
имели бы 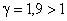 , и следовало бы двигаться в сторону увеличения
, и следовало бы двигаться в сторону увеличения 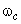 .
.
Отметим,
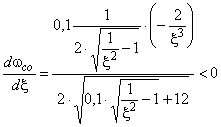 ,
,
то есть 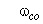 убывает с ростом
убывает с ростом 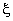 .
.
Из приведенного с очевидностью вытекает следующая методика настройки параметров авиационного тренажера. А именно, для улучшения класса системы, имеющей параметры 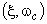 , необходимо:
, необходимо:
- вычислить 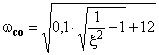 ,
,
- сравнить 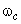 со значением
со значением 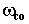 ,
,
- выбрать шаг 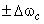 и взять вместо
и взять вместо 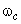 значение
значение 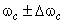 ,
,
- вычислить 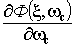 ,
,
- вычислить 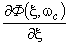 ,
,
- вычислить шаг 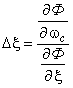 ,
,
- двигаться в этом направлении, пока 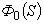 убывает,
убывает,
- уточнить направление вектора-градиента в предпоследней точке 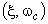 , где значение
, где значение 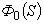 было меньше последнего,
было меньше последнего,
- повторить процедуру сначала.
Предложенный подход эффективно использовался и при многокритериальной оптимизации сложных систем различного назначения [5…8].
Литература:
1. Данилов А. М., Гарькина И. А. Сложные системы: идентификация, синтез, управление: монография. — Пенза: ПГУАС, 2011. — 308 с.
2. Данилов А. М.,Гарькина И. А., Домке Э. Р. Математическое и компьютерное моделирование сложных систем. — Пенза: ПГУАС, 2011. -296 с.
3. Данилов А. М., Гарькина И. А., Домке Э. Р. Математическое моделирование управляющих воздействий оператора в эргатической системе / Вестник МАДИ, № 2, 2011. –С.18–23
4. Гарькина И. А., Данилов А. М., Пылайкин С. А. Транспортные эргатические системы: информационные модели и управление / Мир транспорта и технологических машин. — 2013. -№ 1 (40). — С. 115–122.
5. Гарькина И. А., Данилов А. М. Управление в сложных технических системах: методологические принципы управления / Региональная архитектура и строительство, № 1 (12), 2012, С.39–43.
6. Будылина Е. А., Гарькина И. А., Данилов А. М., Сухов Я. И. Некоторые подходы к анализу и синтезу сложных систем / Молодой ученый. — № 10(57). — 2013. — С.105–107.
7. Будылина Е. А., Гарькина И. А., Данилов А. М., Махонин А. С. Основные принципы проектирования сложных технических систем в приложениях / Молодой ученый. — № 5. 2013. –С.42–45.
8. Гарькина И. А., Данилов А. М., Домке Э. Р. Промышленные приложения системных методологий, теорий идентификации и управления / Вестник МАДИ. — 2009. — № 2(17). — С.77–82.

