Современная судовая электроника ВМФ включает навигационные комплексы, блоки управления двигателем, системы связи (радиостанции, антенны, системы GMDSS, ИНМАРСАТ, НАВАРЕА и прочие). К ней предъявляются высокие требования, связанные со спецификой эксплуатации. Особое внимание уделяется пассивным электронным устройствам систем связи.

Сферический конденсатор — это пассивный физический объект электрической цепи, который конструктивно изготовляют в виде проводников, разделенных однородным изотропным диэлектрическим слоем. Толщина изоляционной прослойки мала в сравнении с размерами обкладок. Устройство используется для накопления больших зарядов и достижения разности потенциалов в несколько мегавольт. Он применяется в высоковольтных источниках питания с большим выходным напряжением и малым током для установок по ремонту специальной техники, является значимой частью различных устройств цепей с частотно-зависимыми свойствами [1].

Принцип работы сферического конденсатора основан на использовании созданного между его обкладками электрического поля.

Подключение электродов сферического конденсатора к источнику напряжения (постоянного, переменного) приводит к его зарядке: положительный заряд скапливается на внутренней сфере, а отрицательный заряд — на внешней обкладке. Между обкладками возникает разность потенциалов

(1)

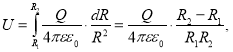
где Q — электрический заряд; ε — диэлектрическая постоянная вакуума; ε ₀ — диэлектрическая проницаемость среды; и — радиусы внутренней и внешней обкладок сферического конденсатора соответственно.

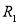
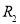
Модуль напряженности этого поля определяется выражением

(2)

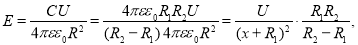
где С — ёмкость; U — приложенное напряжение; — расстояние от центра конденсатора, — радиус внутренней обкладки сферического конденсатора, х — расстояние от поверхности внутренней сферы до точки наблюдения; ε — диэлектрическая постоянная вакуума; ε ₀ — диэлектрическая проницаемость среды.

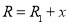
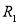
Как видно из равенства (2), эта характеристика электрического поля определяется геометрией устройства, приложенным напряжением и положением точки наблюдения от поверхности внутренней обкладки конденсатора.

Радиусы обкладок, диэлектрическая проницаемость изоляционного материала определяют модуль электроёмкости сферического конденсатора. С ростом размеров сферических проводников увеличивается ёмкость устройства. Диэлектрический сферический слой повышает эффективность устройства, уменьшая влияние совокупности внешних факторов на процесс накопления электрического заряда и энергии электрического поля

. (3)

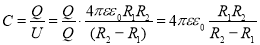
Согласно условию статического распределения заряда в пределах внутренней сферической обкладки конденсатора напряженность поля будет равна нулю (Е = 0 В/м), поэтому

(4)

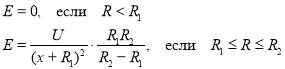
С учетом системы уравнений (4), условия статического распределения заряда для точек, расположенных на расстоянии x от поверхности внутренней обкладки на отрезке с шагом 0,5 см, на рис. 1 представлена зависимость напряженности электрического поля сферического конденсатора от расстояния до центра конденсатора. Параметры конденсатора: . Приложенное напряжение

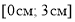
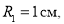
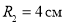
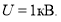
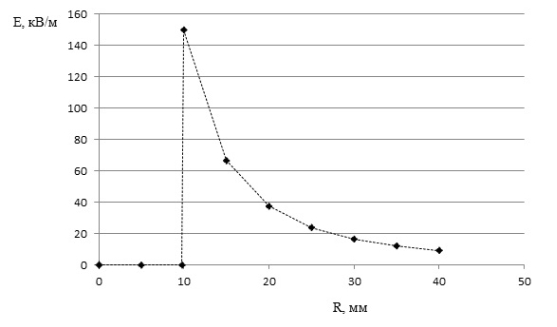
Рис. 1. Напряженность электрического поля сферического конденсатора

Как видно из рис. 1, в пределах внутренней обкладки сферического конденсатора поля нет. Затем напряженность поля скачком достигает максимума и уменьшается обратно пропорционально квадрату расстояния до внутренней обкладки конденсатора.

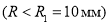
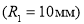
Согласно теореме Гаусса [2, с. 162] электрическое поле заряженного тела вращения симметрично во всех равноудаленных точках от его геометрического центра. Следовательно, объемная плотность энергии [2, с. 178] для них одинакова и зависит от силовой характеристики поля.

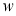
Полная энергия в сферической диэлектрической прослойке радиусами и определяется выражением

(5)

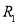
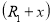
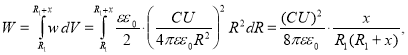
где R — радиус слоя; dR — толщина слоя; — элементарный объём слоя; — объемная плотность энергии.

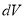
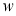
Как видно из равенства (5), полная энергия электрического поля сферического конденсатора определяется ёмкостью устройства, приложенным напряжением, положением точки наблюдения от поверхности внутренней обкладки конденсатора, радиусом внутренней обкладки.

Найдем энергию электрического поля сферического конденсатора емкостью С = 1 нФ, если , , . Диэлектриком является калиевая слюда (ε = 6). Исследуем точки, расположенные на расстоянии x от поверхности внутренней обкладки на отрезке с шагом 0,5 см.

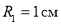
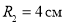
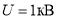
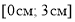
Условие статического распределения заряда требует, чтобы в пределах внутренней сферической обкладки конденсатора энергия электрического поля была равна нулю, т. к. напряженность поля равна нулю, поэтому

(6)

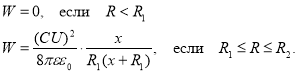
С учетом системы уравнений (6), условия статического распределения заряда на рис. 2 представлена зависимость энергии электрического поля сферического конденсатора от расстояния до центра конденсатора.

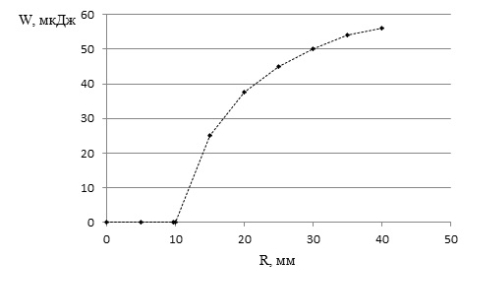
Рис. 2. Энергия электрического поля сферического конденсатора

Как видно из рис. 2, в пределах внутренней обкладки сферического конденсатора электрической энергии поля нет. Затем энергия растет по нелинейному закону в пределах исследуемого устройства.

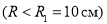
Таким образом, в ходе нашей работы мы получили модельраспределения электрического поля в сферическом конденсаторе, рассчитав напряженность электрического поля и энергию этого поля. Полученные знания базовых принципов функционирования сферического конденсатора, свойств его электростатического поля позволят в дальнейшей профессиональной деятельности эффективно эксплуатировать сложные технические комплексы ВМФ и ВВС РФ, содержащие это устройство.

Литература:

1. Сферический генератор на ЭСК. Расчёт: [Электронный ресурс]. URL: https //gorchilin.com/articles/energy/condenser_3 (дата обращения 27.07. 2019)
2. Трофимова Т. И. Курс физики. М.: Академия, 2019. 541 с.