Одним из направлений исследований физики атмосферы является атмосферное электричество. Вблизи поверхности Земли существует область, описание электрических процессов которой отличается от описания этих процессов в свободной атмосфере — это область приземного слоя атмосферы. В приземном слое существенное влияние на распределение электрических характеристик оказывают турбулентные процессы обмена, наличие поверхностных источников радиоактивных веществ, свойства подстилающей поверхности, наличие аэрозольных частиц. [1]

Важность явлений, происходящих в приземном слое, обусловлена в первую очередь тем, что в нижних слоях атмосферы сосредоточена значительная часть человеческой деятельности. Понимание протекающих в этих слоях процессов является основой для разработки методов контроля антропогенного воздействия на атмосферу в целом.

Анализируя результаты компьютерного моделирования, можно сказать, что определенный интерес представляет выявление функциональной зависимости напряженности электрического поля приземной атмосферы не только от вертикальной координаты , но и от значения напряженности на поверхности земли при различных значениях степени ионизации воздуха . [3] Следовательно, необходимо получить зависимость вида:

(1)

Согласно теоретическим представлениям, поле в вертикальных масштабах изменяется согласно уравнению Пуассона [1]:

(2)

Значит, напряженность электрического поля атмосферы по мере удаления от земной поверхности изменяется по закону степенной функции. Результаты численного эксперимента будем аппроксимировать полиномиальной регрессией, степень полинома выберем , тогда уравнение зависимости поля от заданной на поверхности земли значения напряженности в общем виде выглядит следующим образом:

.(3)

Тогда, вектор коэффициентов для построения полиномиальной регрессии в системе MathCAD [2] рассчитывается как:

(4)

где, вектор данных аргумента — ; вектор экспериментальных значений напряженности электрического поля атмосферы — ; порядок аппроксимирующего полинома — .

Далее, чтобы получить результат полиномиальной регрессии, нужно использовать встроенную функцию — «interp»:

.(5)

На рис. 1 показано сравнение исходной и аппроксимирующей кривой.

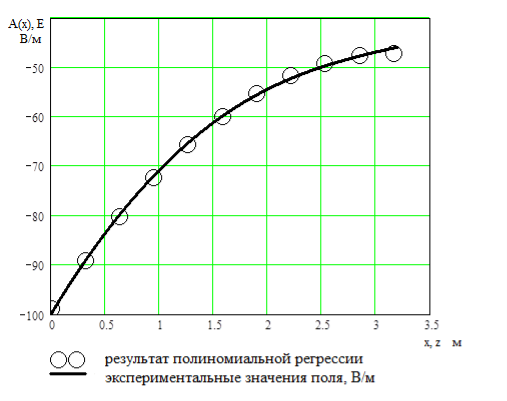
Рис. 1. Аппроксимация полиномиальной функцией

По формуле (4) получаем коэффициенты полиномов, представленные в таблице 1, для уравнений вида:

(6)

Таблица 1

Коэффициенты полиномиальной регрессии

Дальнейшие рассуждения проведем на примере с . Запишем уравнения зависимости поля от вертикальной координаты в виде (6):

,

(7)

.

Система уравнений зависимости поля от значения напряженности на поверхности земли, согласно уравнению (3) будет иметь вид:

,

(8)

.

Поскольку необходимо найти функциональную зависимость вида (1),приравниваем правые части соответственно уравнений систем (7) и (8) получаем:

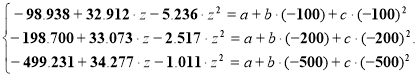(9)

Система (9) решалась в MathCAD, используя ключевые команды «Given» и «Find». Коэффициенты получаются равными:

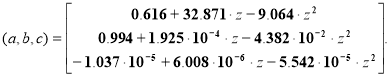(10)

Теперь, подставляя найденные значения коэффициентов в уравнение (3), получим зависимость поля как функцию напряженности электрического поля на поверхности земли и вертикальной координаты :

(11)

Таким образом, получена функция отклика (11), зависящая от двух факторов: напряженности на поверхности земли и вертикальных масштабов изменения при заданном уровне интенсивности ионообразования . Трехмерным графиком уравнения (11) будет так называемая, поверхность «отклика». На рис. 2 показана поверхность , являющаяся решением уравнения (11). Фактически, поверхность это математическая модель электрического поля в приземном слое атмосферы с учетом влияющего фактора .

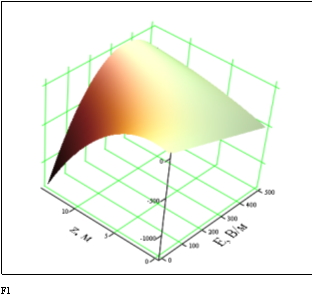
Рис. 2. Поверхность отклика F1 для уравнения (11)

Аналогичные рассуждения позволили рассчитать и получить модели вида (1) для остальных значений параметра :

при

(12)

при

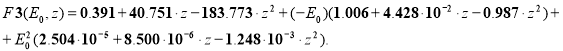(13)

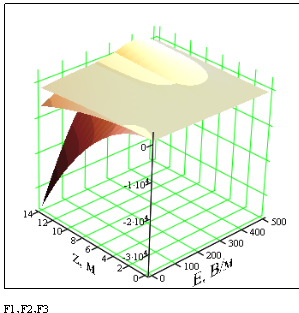
Рис. 3. Поверхности вида Сверху — вниз: при , при при

В таблице 2 представлены результаты численного эксперимента и модельные расчеты напряженности электрического поля атмосферы для уравнения (11) при .

Таблица 2

Экспериментальные имодельные значения напряженности электрического поля атмосферы

Модели могут использоваться для определения значения напряженности электрического поля атмосферы на любой высоте в пределах характерного слоя без проведения дополнительных численных решений систем уравнений, описывающих электрическое состояние приземного слоя атмосферы.

Литература:

1. Морозов В. Н. Атмосферное электричество / В. Н. Морозов // Атмосфера. Справочник (справочные данные, модели). – Л.: Гидрометеоиздат, 1991. С. 394–408.
2. Кирьянов Д. В. Самоучитель MathCAD 2001 / Д. В. Кирьянов. — СПб.: БХВ-Петербург, 2001. 544 с.
3. Кофи Дж. Экспериментальные данные о пограничном слое атмосферы / Дж. Кофи // Атмосферная турбулентность и моделирование распространения примесей. — Л.: Гидрометеоиздат, 1985. С. 126–172.