Введение

Во многих задачах, особенно в задачах прикладного характера, которые возникают в связи с решением самых разнообразных практических проблем, возникает вопрос приближения математической модели исследуемого объекта на конкретном множестве. К таким задачам следует отнести и приближение функций со спектром из специальных семейств множеств, которые моделируют требуемую область аппроксимируемой функции.

В силу ограниченности диапазона восприятия приборов, диапазона восприятия органов чувств самого человека, ограниченности необходимого временного промежутка при исследовании математической модели часто бывает достаточно найти приближение искомого объекта не на всей числовой прямой, а на некотором промежутке, отражающем необходимый диапазон восприятия.

В данной статье рассматривается приближение периодических функций тригонометрическими полиномами со спектром из множеств, называемых гармоническими интервалами. Гармонические интервалы в некоторой степени моделируют такие промежутки и оказывают помощь в решении задач такого рода.

Вспомогательные сведения

Определение 1. [1]Пусть Множество вида

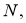
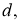
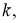
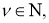
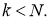
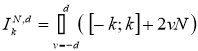
назовем гармоническим отрезком в Множество вида

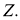
назовем гармоническим интервалом в

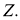
Множество всех тригонометрических полиномов порядка обозначается через [2]. Определим через и множества тригонометрических полиномов вида

,

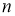
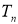
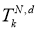
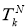
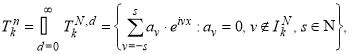
где  действительные числа, и назовем и множеством тригонометрических полиномов по гармоническому отрезку и множеством тригонометрических полиномов по гармоническому интервалу соответственно.

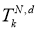
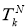
Определение 2. [1] Величину назовем наилучшим приближением по гармоническому интервалу функции тригонометрическими полиномами из порядка меньше или равного

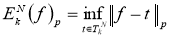
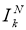
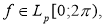
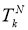
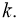
Аналогично определяется наилучшее приближение по гармоническому отрезку функции полиномами из порядка меньше или равного

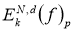
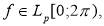
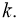
Определение 3. Тригонометрический полином обладающий свойством , назовем многочленом наилучшего приближения функции по гармоническому отрезку .

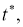
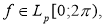
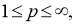
Свойства наилучших приближений периодических функций

Лемма 1. Пусть , тогда для наилучших приближений по гармоническим отрезкам и гармоническим интервалам справедливо следующее соотношение

.

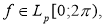
Доказательство . Рассмотрим последовательность Так как , то по определению и для любых справедливо неравенство то есть рассматриваемая последовательность является невозрастающей и ограничена снизу. Следовательно, последовательность имеет предел конечный при

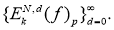
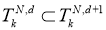
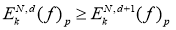
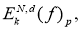
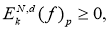
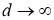
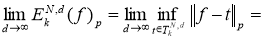
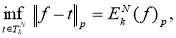
что и требовалось доказать.

Лемма 2. Пусть , тогда существует многочлен такой, что справедливо равенство

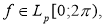
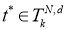
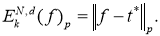
Доказательство. По определению для любого существует полином , где — действительные числа, такой, что выполняется неравенство

(1)

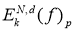
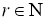
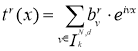
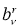
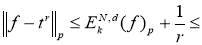
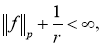
тогда следует, что

(2)

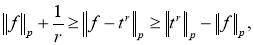
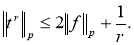
Последовательно применяя неравенство Гельдера [3] и (2), получим, что для любого и для любого выполняется соотношение

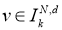
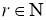
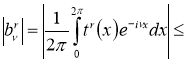
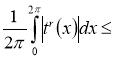
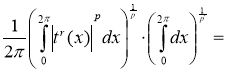
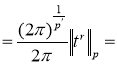
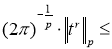
то есть последовательность ограничена для любых . Следовательно, из этой последовательности можно выделить сходящуюся подпоследовательность такую, что

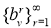
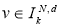
Далее, из можно выделить сходящуюся подпоследовательность такую, что и так далее до момента, когда найдем подпоследовательность , где такую, что

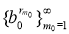
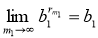
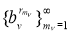
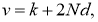
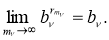
Последние номера удовлетворяют всем предыдущим условиям, так как выбраны из каждого предпоследнего множества, и поэтому по ним сходятся все последовательности . для любого .

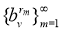
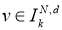
Таким образом, имеем для любого

. (3)

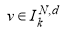
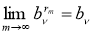
Далее, пусть тогда получаем

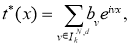
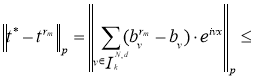
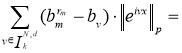
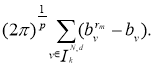
В силу (3) имеем Так как то из (1) получим

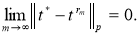
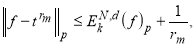
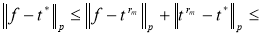
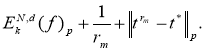
Предельный переход в этом неравенстве при дает неравенство вида

.

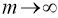
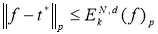
С другой стороны, по определению , имеем соотношение

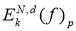
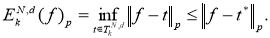
Из последних двух неравенств получаем искомое равенство

где , что и требовалось доказать.

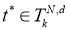
Теорема 1. Пусть , тогда наилучшее приближение по гармоническому интервалу обладает свойствами

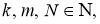
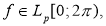
1.

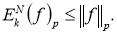
2. .

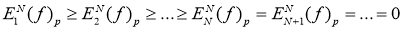
3. Если , то при

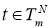
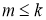
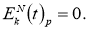
4. Если с = const, то выполняется соотношение .

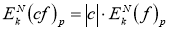
5. ,

6. Если , то при верно равенство

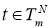
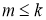
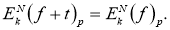
Доказательство.

1. Принимая во внимание, что , получаем

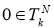
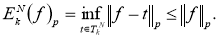
2. Так как при и , то свойство 2 следует из определения инфимума.

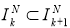
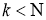
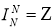
3. Это свойство следует из определения .

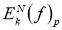
4. Если , то свойство 4 следует из свойства 3. Пусть и  многочлен наилучшего приближения функции по гармоническому отрезку . Тогда, согласно леммам 1 и 2, имеем

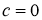
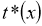
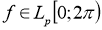
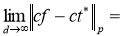
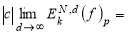
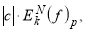
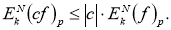
С другой стороны,

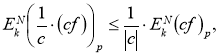
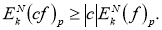
В результате получили свойство 4.

5. По лемме 1 имеем

,

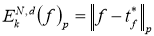
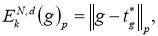
тогда получаем, что

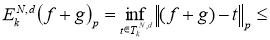
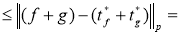
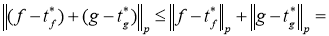
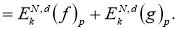
Переходя в последнем неравенстве к пределу при и используя лемму 1, находим требуемое свойство 5.

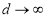
6. Из свойств 3 и 5 имеем

.

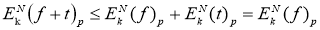
Свойства 3, 4, 5 дают

.

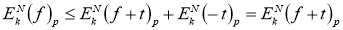
Таким образом, получили свойство 6. Лемма доказана.

Заключение

В представленной работе введены элементы теории приближений для гармонических отрезков и гармонических интервалов, исследованы свойства наилучших приближений периодических функций со спектром из гармонических отрезков и гармонических интервалов.

Литература:

1. Есенбаева Г. А., Есбаев А. Н., Сыздыкова Н. К., Смирнова М. А. On the function approximation by trigonometric polynomials and the properties of families of function classes over harmonic intervals // Bulletin of the Karaganda University. Mathematics Series. — 2023. — № 3(111). — С. 181–190.

2. Даугавет И. К. Введение в классическую теорию приближения функций. — Санкт-Петербург: Санкт-Петербургский гос. ун-т, 2011.

3. Хелемский А. Я. Лекции по функциональному анализу. — М.: МЦНМО, 2014.