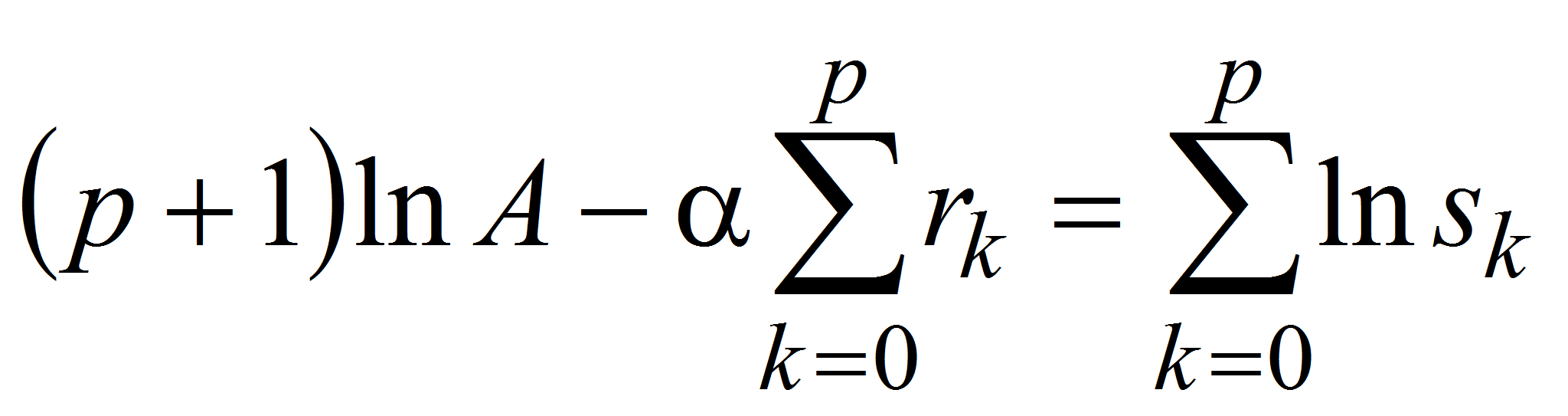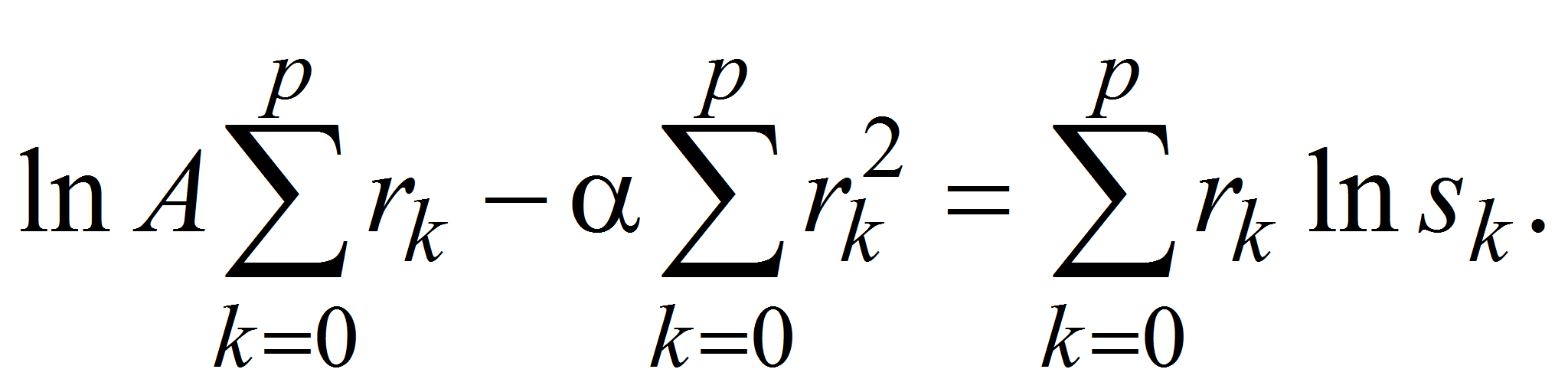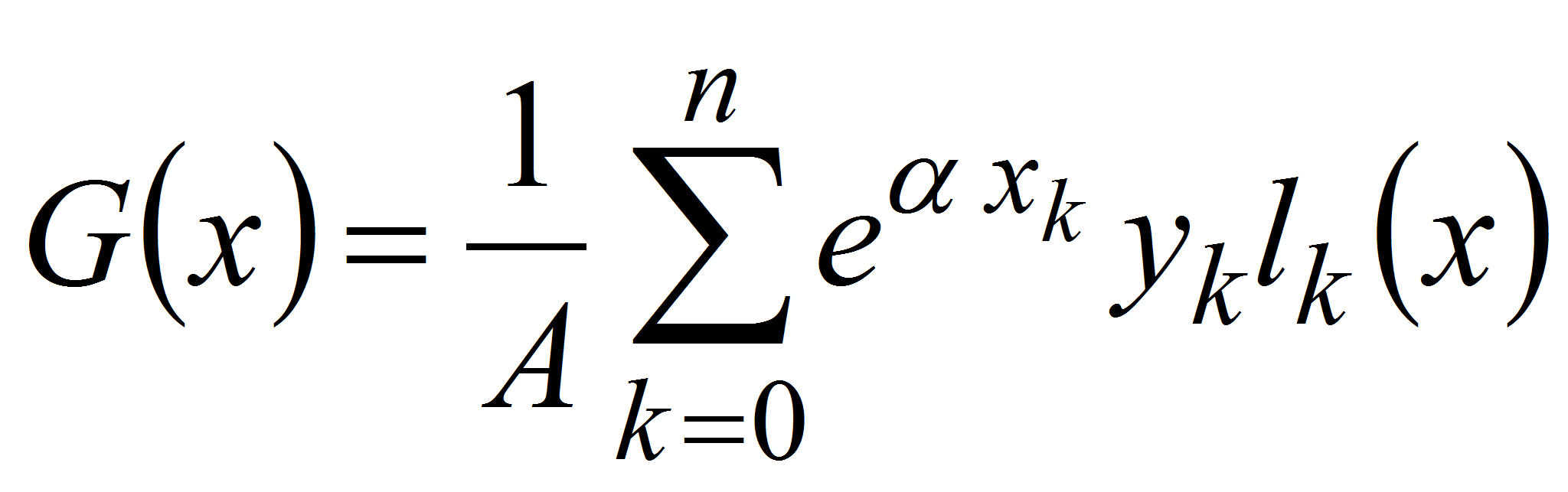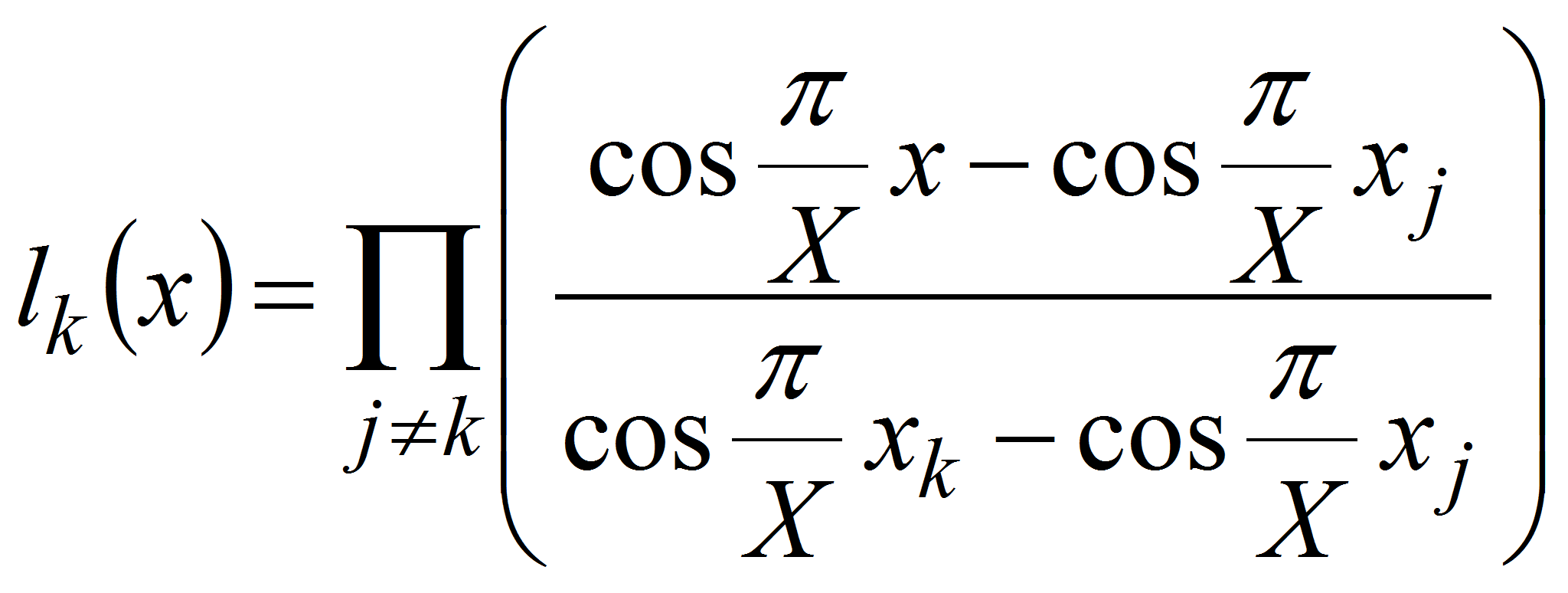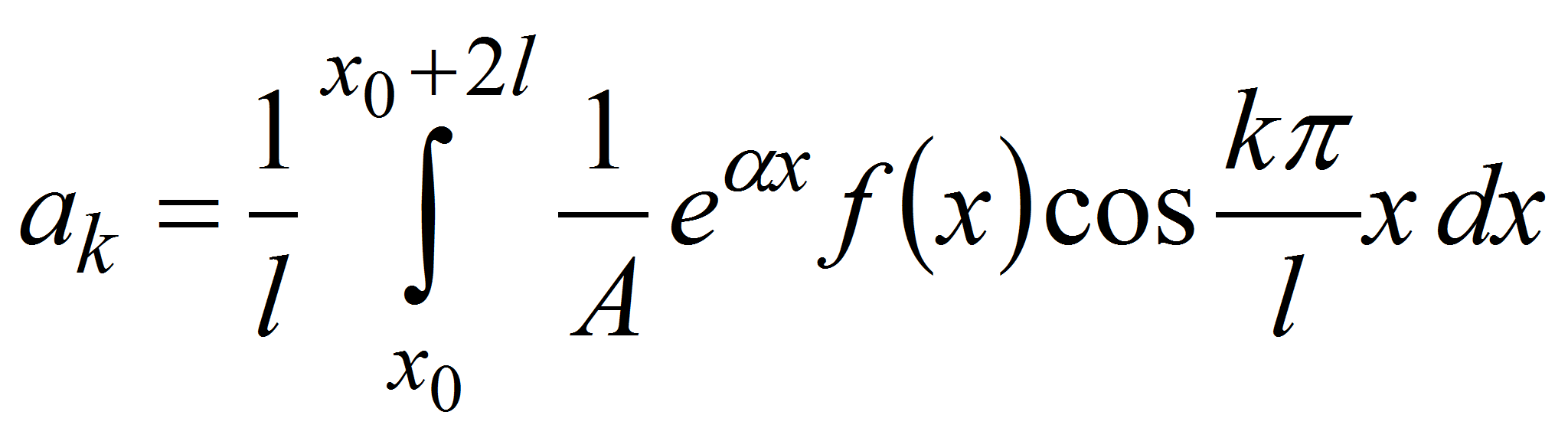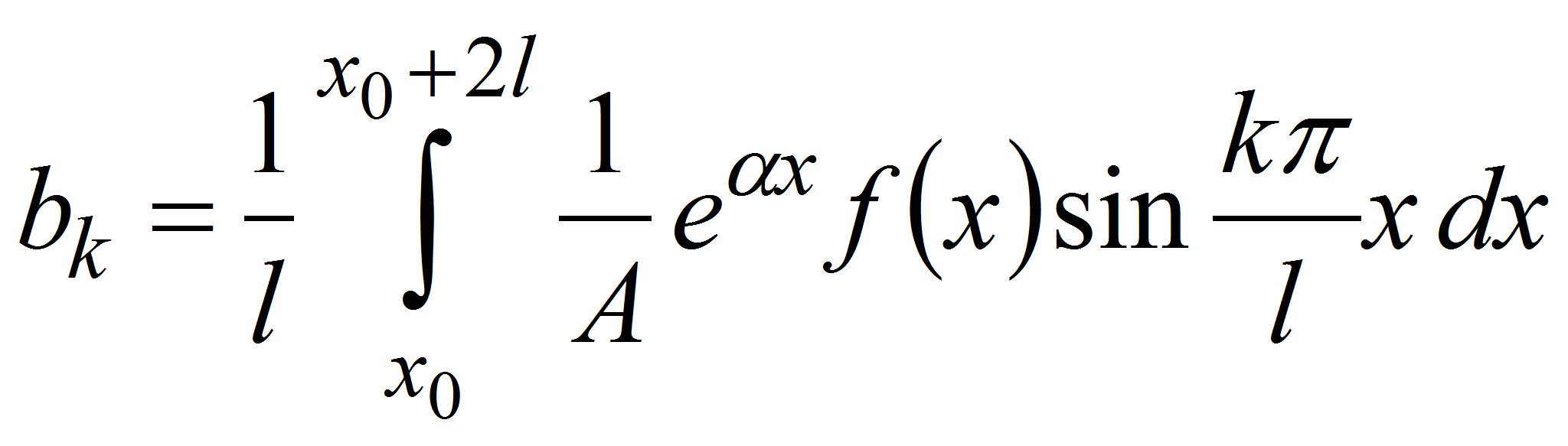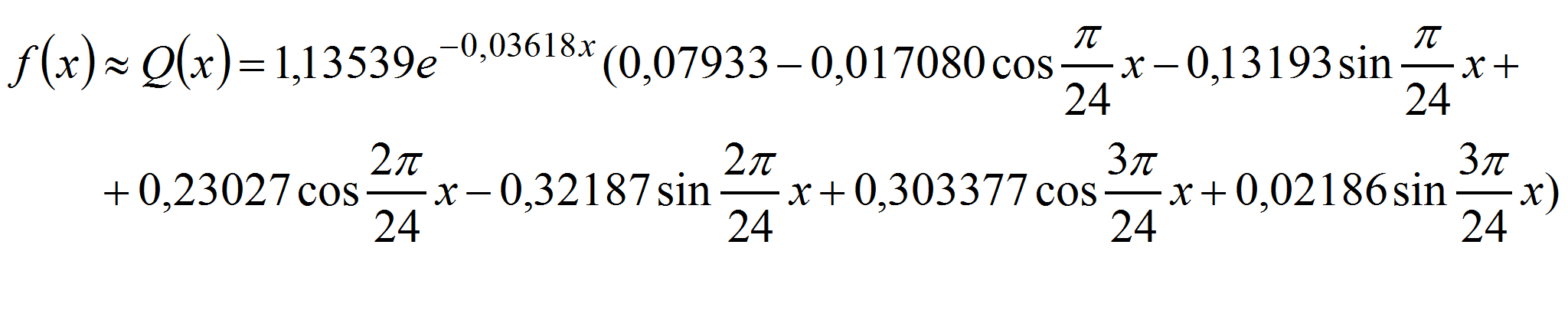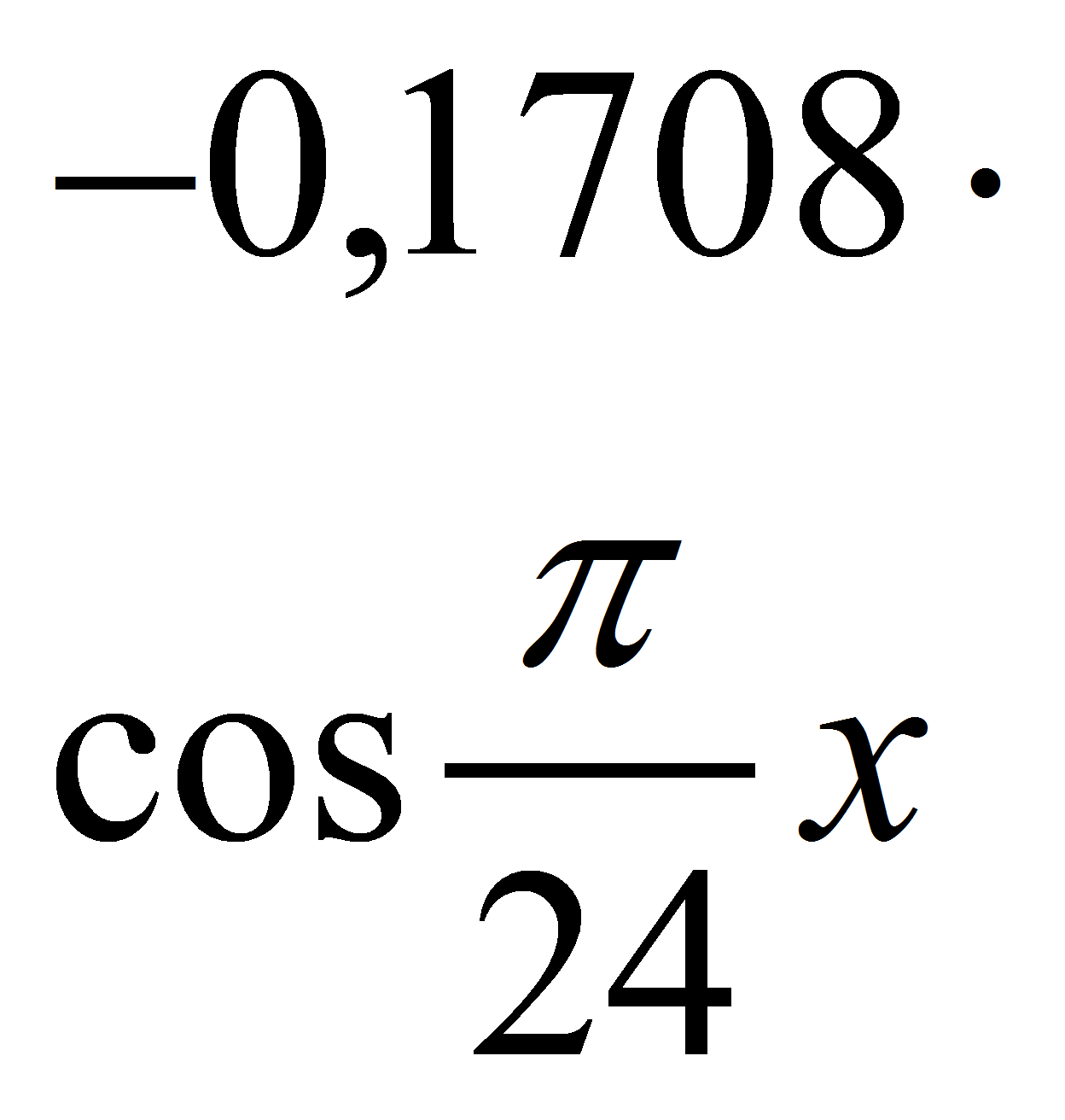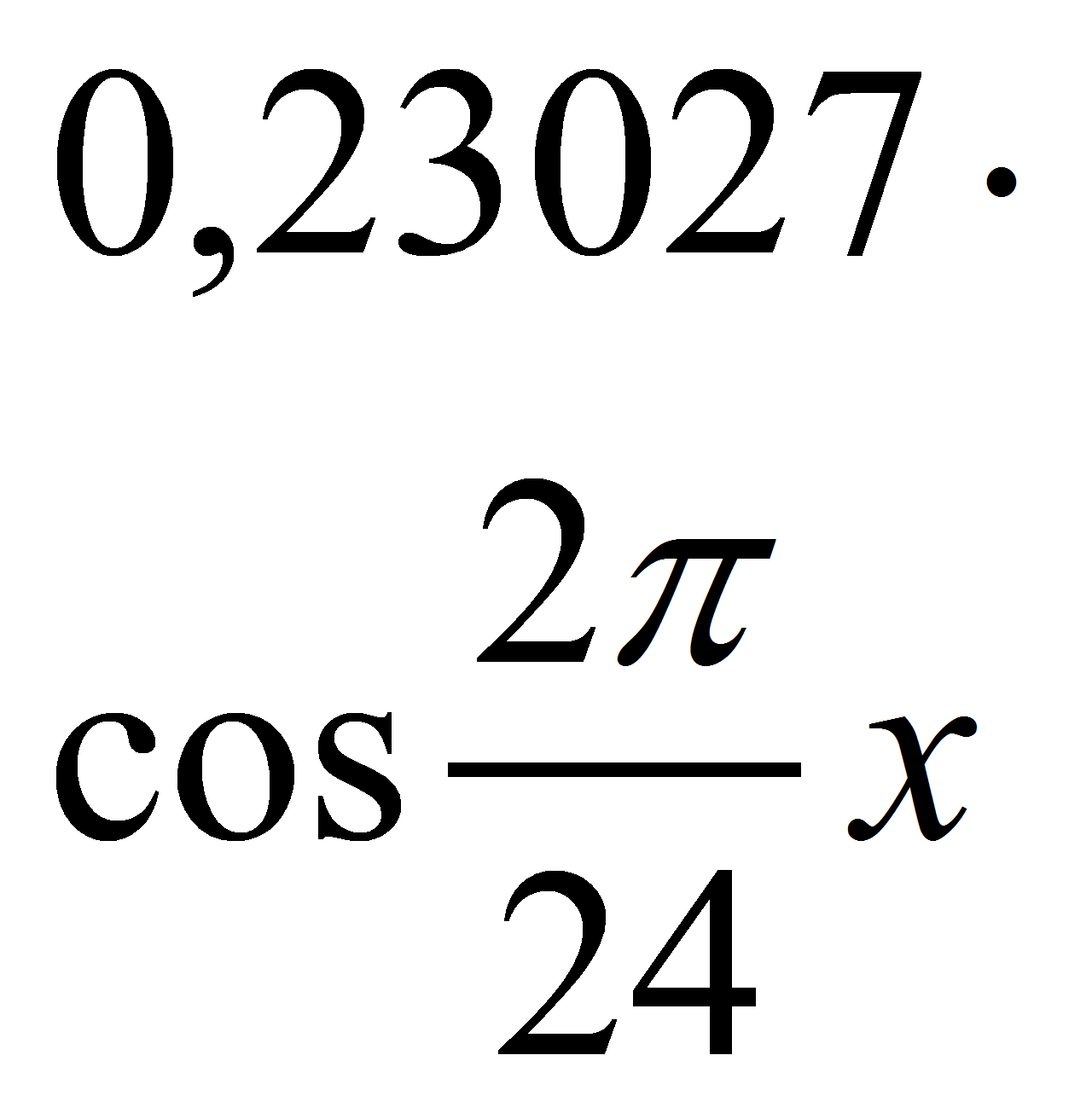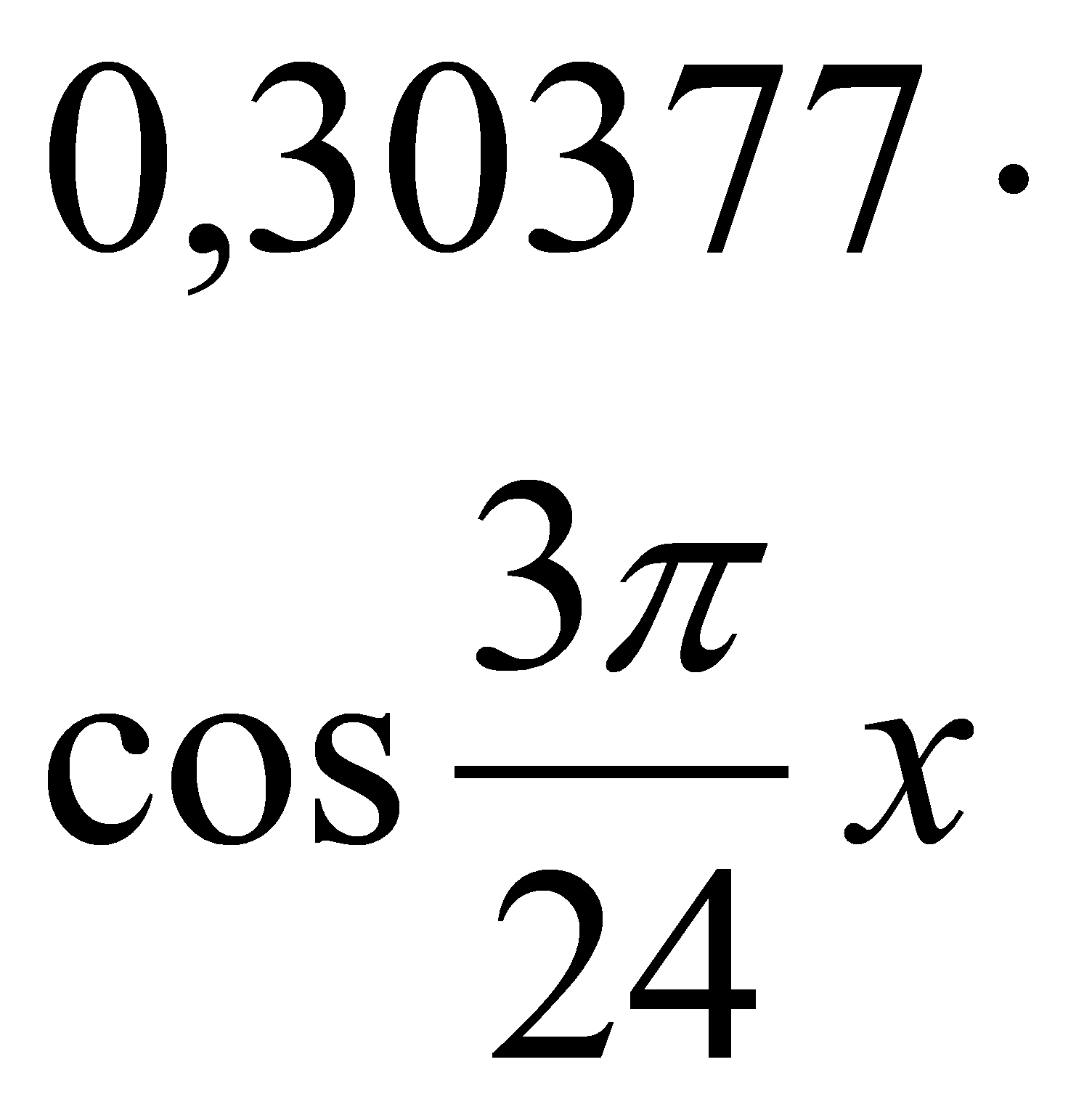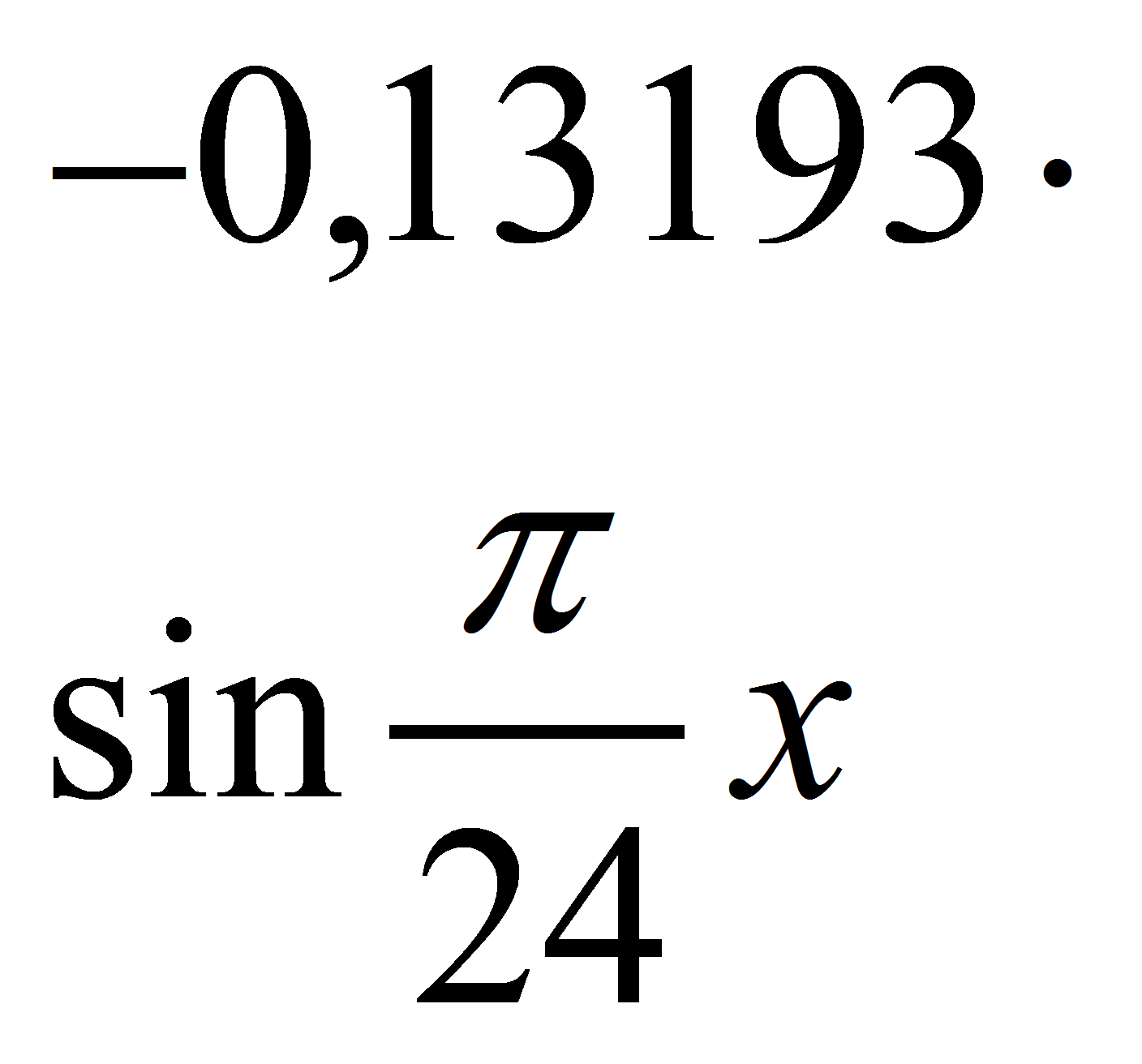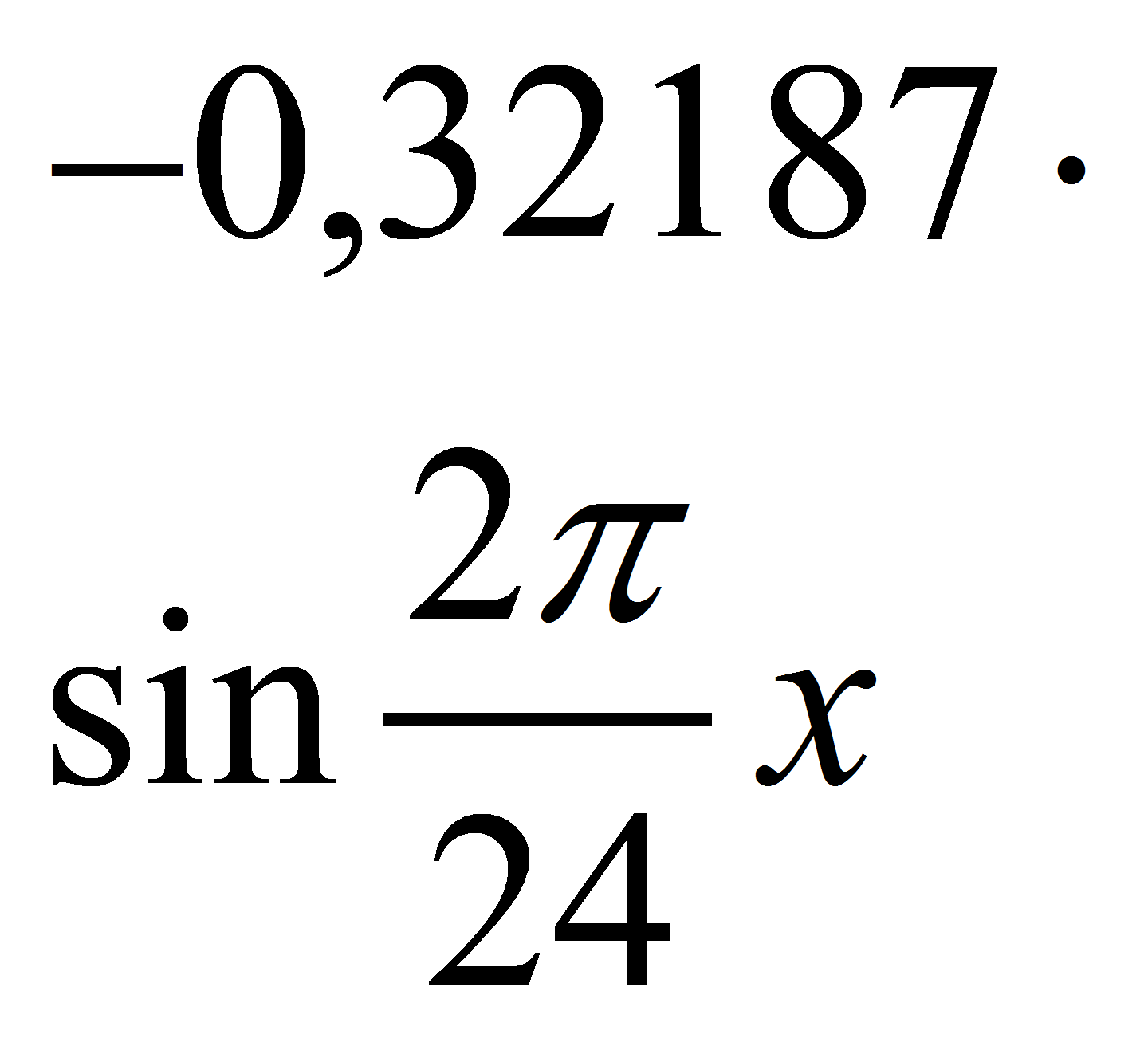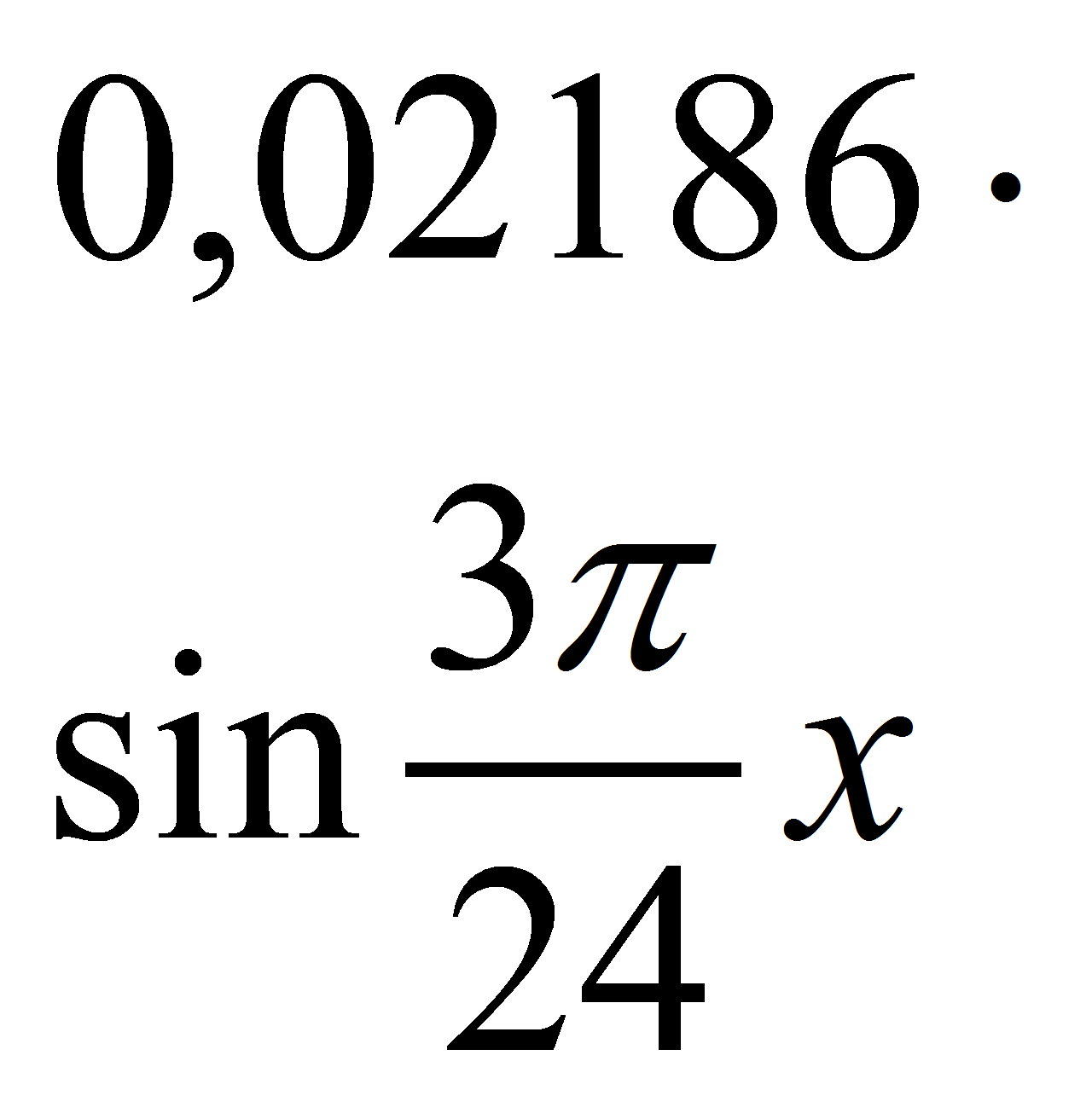Анализ и синтез сложных конструкций во многих
случаях связаны с построением вибрационной карты и селекцией
конструктивных элементов с недопустимым уровнем вибрации.
Положительный эффект при решении этих задач дает использование метода
экспоненциально-тригонометрической аппроксимации функции
![]() ,
заданной таблично (экспериментальные данные) на отрезке
,
заданной таблично (экспериментальные данные) на отрезке
![]() .
Для определенности будем искать приближение
.
Для определенности будем искать приближение
![]() выражением вида
выражением вида
где
![]() –
чётный тригонометрический полином. Для определения параметров
–
чётный тригонометрический полином. Для определения параметров
![]() и α экспоненциального
множителя
и α экспоненциального
множителя
![]() построим огибающую заданной функции, выделив из конечной
последовательности модулей заданных значений функции строго
убывающую, вогнутую последовательность ординат:
построим огибающую заданной функции, выделив из конечной
последовательности модулей заданных значений функции строго
убывающую, вогнутую последовательность ординат:
-
построим (конечную) последовательность модулей заданных значений
функций
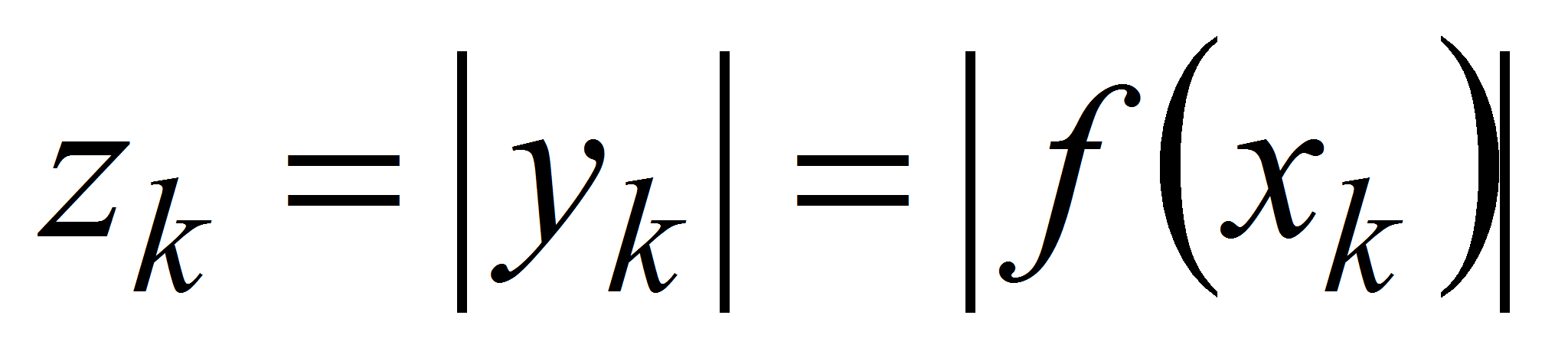 ,
, ;
; -
извлечём из этой последовательности строго убывающую
последовательность
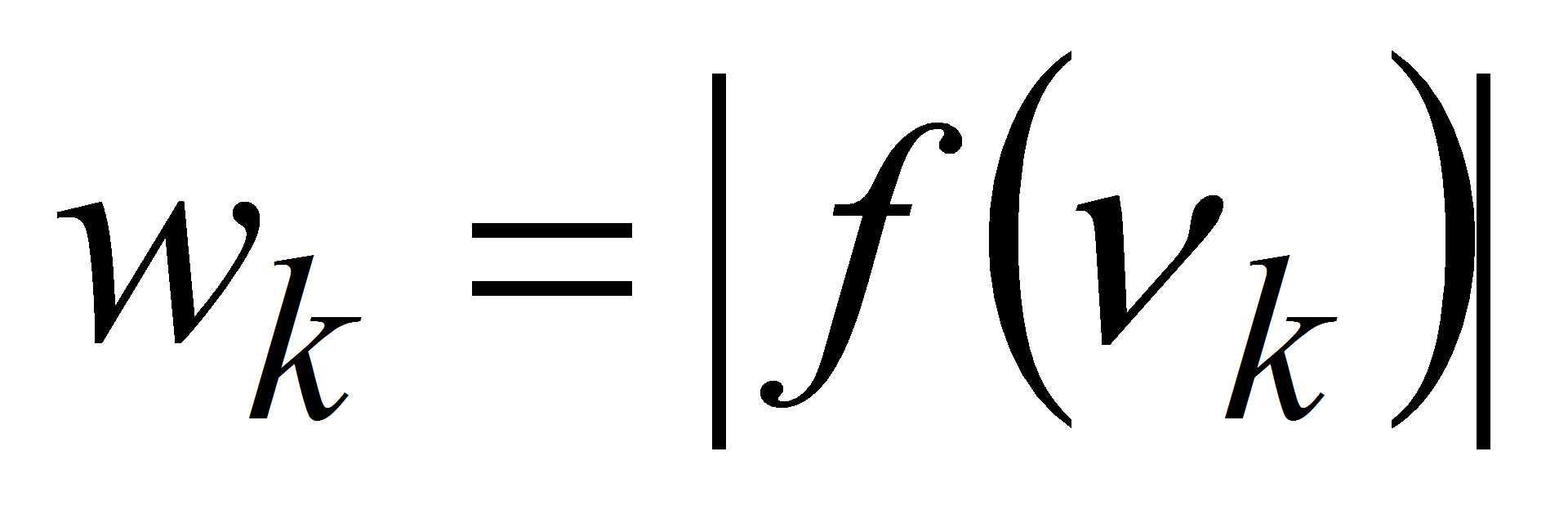 ,,
сравнивая поочерёдно смежные члены; если данный член окажется не
меньше предыдущего, то все предыдущие члены, которые не больше
данного, исключаются;
,,
сравнивая поочерёдно смежные члены; если данный член окажется не
меньше предыдущего, то все предыдущие члены, которые не больше
данного, исключаются; -
из полученной последовательности извлечем строго вогнутую
последовательность
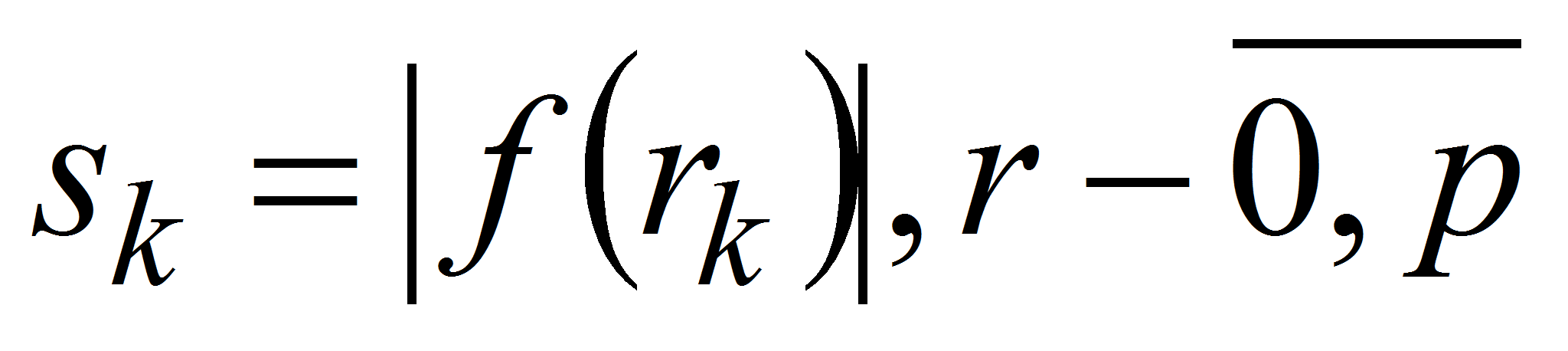 ,
сравнивая поочерёдно угловые коэффициенты смежных звеньев полученной
ломаной; если данный угловой коэффициент не больше предыдущего, то
исключим все те предыдущие вершины ломаной, которые окажутся, ниже
прямой, продолжающей влево данное звено. Ординаты вершин полученной
ломаной и дадут требуемую конечную строго убывающую, строго
вогнутую последовательность
,
сравнивая поочерёдно угловые коэффициенты смежных звеньев полученной
ломаной; если данный угловой коэффициент не больше предыдущего, то
исключим все те предыдущие вершины ломаной, которые окажутся, ниже
прямой, продолжающей влево данное звено. Ординаты вершин полученной
ломаной и дадут требуемую конечную строго убывающую, строго
вогнутую последовательность
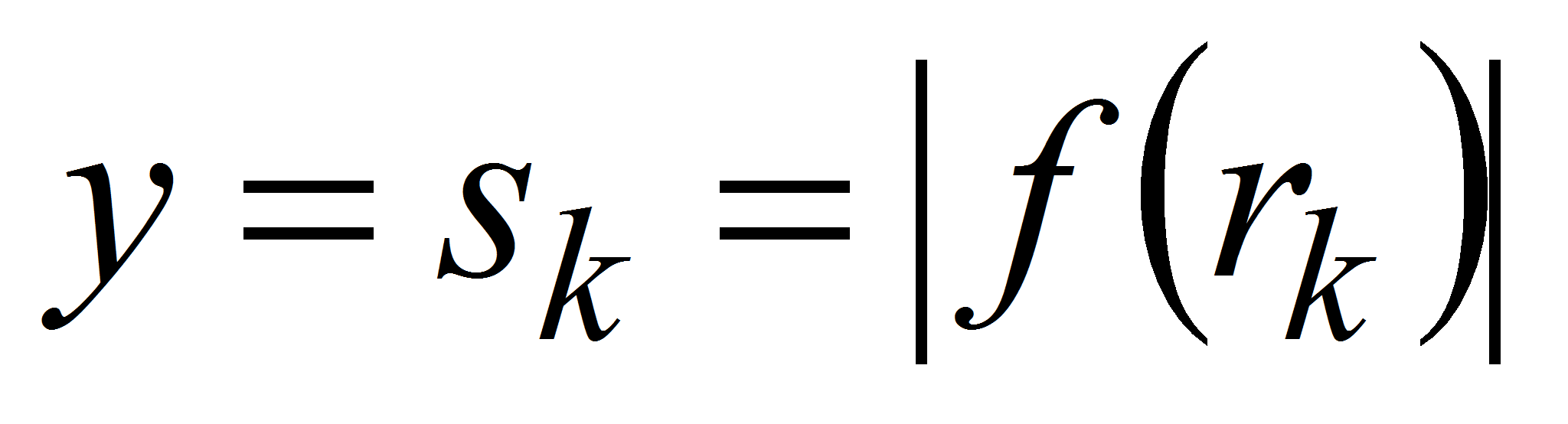 , где
, где
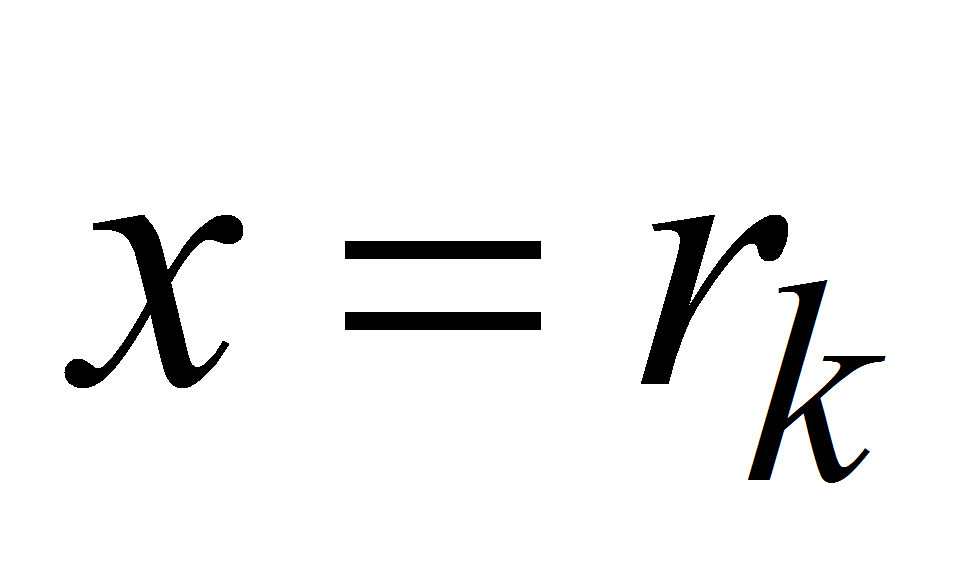 -
отобранные значения независимой переменной
-
отобранные значения независимой переменной
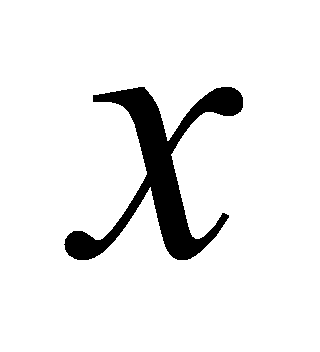 ,
,
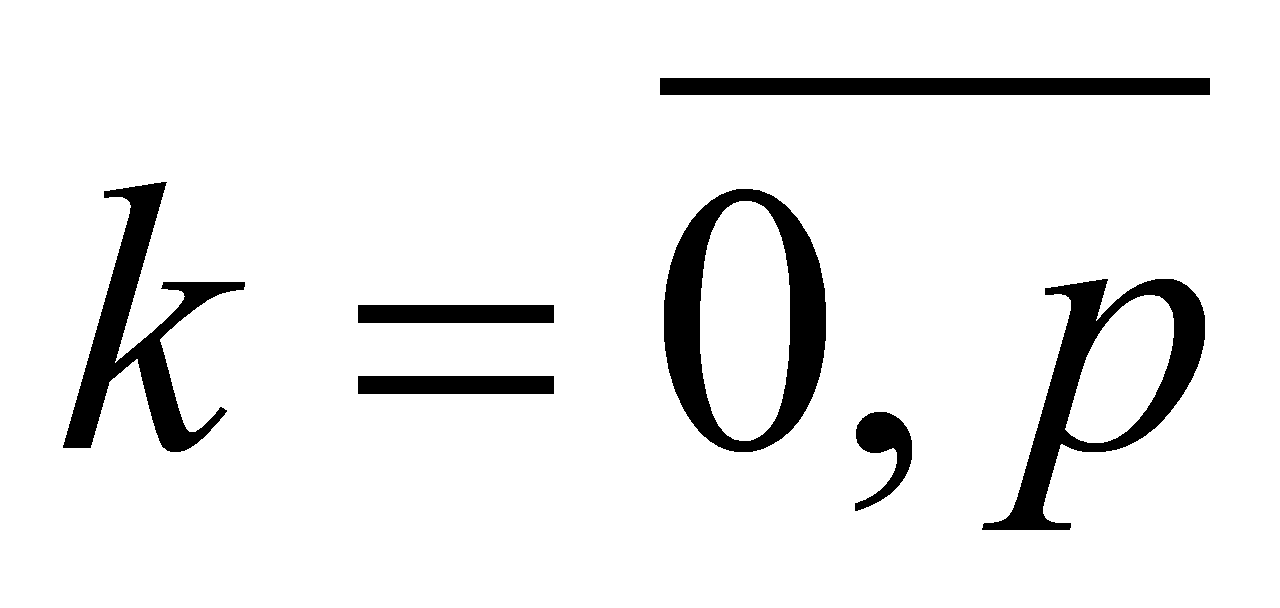 .
.
Далее полученную зависимость
![]() ,
,
![]() аппроксимируем экспоненциальной функцией методом наименьших
квадратов. Параметры A и α
определятся из системы уравнений
аппроксимируем экспоненциальной функцией методом наименьших
квадратов. Параметры A и α
определятся из системы уравнений
Затем по заданной таблице значений функции
![]() построим таблицу значений функции
построим таблицу значений функции
![]() и интерполируем величину t чётным тригонометрическим
полиномом
и интерполируем величину t чётным тригонометрическим
полиномом
Окончательно:
В качестве иллюстрации рассмотрим экспоненциально тригонометрическую
аппроксимацию экспериментальных данных (табличные значения
![]() ,
полученные по осциллограммам, табл.1)
,
полученные по осциллограммам, табл.1)
Таблица 1
|
1 |
0,2967 |
19 |
0,2803 |
37 |
-0,0322 |
55 |
-0,1925 |
73 |
0,0430 |
|
3 |
0,0499 |
21 |
0,1622 |
39 |
-0,0156 |
57 |
-0,1668 |
75 |
0,0517 |
|
5 |
-0,3358 |
23 |
0,0932 |
41 |
0,0315 |
59 |
-0,1060 |
77 |
0,0549 |
|
7 |
-0,7092 |
25 |
0,0794 |
43 |
0,0772 |
61 |
-0,0380 |
79 |
0,0340 |
|
9 |
-0,5298 |
27 |
0,0769 |
45 |
0,0970 |
63 |
0,0366 |
81 |
-0,0100 |
|
11 |
-0,5676 |
29 |
0,0675 |
47 |
0,0717 |
65 |
0,0901 |
83 |
-0,0481 |
|
13 |
-0,1125 |
31 |
0,0409 |
49 |
0,0057 |
67 |
0,1051 |
85 |
-0,0451 |
|
15 |
0,2613 |
33 |
0,0057 |
51 |
-0,0897 |
69 |
0,0835 |
87 |
-0,0519 |
|
17 |
0,5613 |
35 |
-0,0284 |
53 |
-0,1655 |
71 |
0,0535 |
89 |
-0,0313 |
Определим параметры А и α
экспоненциального множителя
![]() (график функции
(график функции
![]() вписывается в область, ограниченную кривыми
вписывается в область, ограниченную кривыми
![]() ,
,
![]() ).
Для этого по заданной последовательности
).
Для этого по заданной последовательности
![]() значений функции, где
значений функции, где
![]() (
(![]() ,
n=44 — четное число)
построим последовательность
,
n=44 — четное число)
построим последовательность
![]() модулей этих значений и из неё извлечём строго убывающую
последовательность
модулей этих значений и из неё извлечём строго убывающую
последовательность
![]() ,
,
![]() .
А именно последовательность:
.
А именно последовательность:
Угловые коэффициенты звеньев полученной ломаной (-0,0336; -0,0097;
-0,0073; -0,0050; -0,0033) строго возрастают; последовательность
![]() совпадает с выделяемой из неё строго убывающей, вогнутой
последовательностью
совпадает с выделяемой из неё строго убывающей, вогнутой
последовательностью
![]() :
:![]() ,
,
![]() ,
,
![]() ;
;![]() .
Аппроксимируем эту последовательность функцией вида
.
Аппроксимируем эту последовательность функцией вида
![]() методом наименьших квадратов, используя результаты, приведенные
в табл.2.
методом наименьших квадратов, используя результаты, приведенные
в табл.2.
Таблица 2
|
k |
l | |||||
|
0 |
1 |
9 |
0,8298 |
81 |
-0,18657 |
-1,67913 |
|
1 |
1 |
17 |
0,5613 |
289 |
-0,57750 |
-9,8175 |
|
2 |
1 |
55 |
0,1925 |
3025 |
-0,64766 |
-90,6213 |
|
3 |
1 |
67 |
0,1021 |
4489 |
-2,25284 |
-150,94028 |
|
4 |
1 |
77 |
0,0549 |
5929 |
-0,90224 |
-223,47263 |
|
5 |
1 |
87 |
0,0519 |
7569 |
-0,29844 |
-257,38428 |
|
∑ |
6 |
312 |
- |
21382 |
-10,525292 |
-733,91522 |
Получим
Откуда:
Далее функцию
![]() аппроксимируем частной суммой
аппроксимируем частной суммой
![]() ряда Фурье, добавляя в неё новые члены до тех пор, пока не будет
достигнута требуемая точность аппроксимации. В рассматриваемом
случае функция
ряда Фурье, добавляя в неё новые члены до тех пор, пока не будет
достигнута требуемая точность аппроксимации. В рассматриваемом
случае функция
![]() на заданном отрезке обнаруживает приблизительную периодичность
с периодом 2l=48=24h.
Рассмотрим разложение на отрезке длиной 2l=48
тригонометрическим полиномом
на заданном отрезке обнаруживает приблизительную периодичность
с периодом 2l=48=24h.
Рассмотрим разложение на отрезке длиной 2l=48
тригонометрическим полиномом
(в данном случае достигается удовлетворительная точность; для достижения большей точности следует добавить новые члены).
Коэффициенты Фурье
приближённо определялись по формуле Симпсона. Для этого составлялись
следующие таблицы (табл.3,4), где
![]() ,
l=24
,
l=24
Таблица 3
|
0 |
1 |
0,2967 |
1,03684 |
0,99144486 |
0,965926 |
0,92338796 |
0,30763 |
|
1 |
3 |
0,0499 |
1,1146414 |
0,92387955 |
0,707107 |
0,38268946 |
0,05562 |
|
2 |
5 |
-0,3358 |
1,198208 |
0,79335337 |
0,258819 |
-0,38268346 |
-0,40238 |
|
3 |
7 |
-0,7092 |
1,2881963 |
0,60876152 |
-0,258819 |
-0,9236796 |
-0,91359 |
|
4 |
9 |
-0,8298 |
1,3848588 |
0,32268346 |
-0,707107 |
-0,9238796 |
-1,14916 |
|
5 |
11 |
-0,5676 |
1,4887745 |
0,13052629 |
-0,965926 |
-0,38268346 |
-0,84503 |
|
6 |
13 |
-0,1125 |
1,6004878 |
-0,13052629 |
-0,965926 |
0,38268346 |
-0,18005 |
|
7 |
15 |
0,2613 |
1,7205837 |
-0,32268346 |
-0,707107 |
0,9238796 |
0,44959 |
|
8 |
17 |
0,5613 |
1,8496913 |
-0,60876152 |
-0,258819 |
0,9238769 |
1,03883 |
|
9 |
19 |
0,2803 |
1,9884867 |
-0,79335337 |
0,258819 |
0,38268346 |
0,55737 |
|
10 |
21 |
0,1622 |
2,1376969 |
-0,92387955 |
0,707107 |
-0,38268346 |
0,34673 |
|
11 |
23 |
0,0932 |
2,298134 |
-0,99144486 |
0,965926 |
-0,9238796 |
0,21419 |
|
12 |
25 |
0,0794 |
2,4705464 |
0,99144486 |
0,965926 |
-0,9238796 |
0,19616 |
|
13 |
27 |
0,0769 |
2,655929 |
-0,32387955 |
0,707107 |
-0,38268346 |
0,20424 |
|
14 |
29 |
0,0675 |
2,8552222 |
-0,79335337 |
0,258819 |
0,38268346 |
0,19273 |
|
15 |
31 |
0,0409 |
3,0694697 |
-0,60876152 |
-0,258819 |
0,9238796 |
0,12554 |
|
16 |
33 |
0,0057 |
3,2997938 |
-0,32268346 |
-0,707107 |
0,9238796 |
0,01881 |
|
17 |
35 |
-0,0284 |
3,5474007 |
-0,13052629 |
-0,965926 |
0,38268346 |
-0,10075 |
|
18 |
37 |
-0,0332 |
3,8135873 |
0,13052629 |
-0,965926 |
-0,38268346 |
-0,12661 |
|
19 |
39 |
-0,0156 |
4,0997478 |
0,32268346 |
-0,707107 |
-0,92387696 |
-0,06396 |
|
20 |
41 |
0,0315 |
4,4073809 |
0,60876152 |
-0,258819 |
-0,92387696 |
-0,13883 |
|
21 |
43 |
0,0772 |
4,7380979 |
0,79335337 |
0,258819 |
-0,38268346 |
0,36578 |
|
22 |
45 |
0,0970 |
5,093631 |
0,92387955 |
0,707107 |
0,38268346 |
0,49408 |
|
23 |
47 |
0,0717 |
5,4758422 |
0,99144486 |
0,965926 |
0,9238796 |
0,39262 |
|
24 |
49 |
0,0057 |
5,8867335 |
0,99144486 |
0,965926 |
0,9238796 |
0,03355 |
Таблица 4
|
0 |
1 |
0,2967 |
1,03684 |
0,13052629 |
0,25881903 |
0,38268343 |
0,30763 |
|
1 |
3 |
0,0499 |
1,1146414 |
0,32268346 |
0,707107 |
0,9238796 |
0,05562 |
|
2 |
5 |
-0,3358 |
1,198208 |
0,60876152 |
0,965926 |
0,9238796 |
-0,40238 |
|
3 |
7 |
-0,7092 |
1,2881963 |
0,793353337 |
0,965926 |
0,38268343 |
-0,91359 |
|
4 |
9 |
-0,8298 |
1,3848588 |
0,92397955 |
0,707107 |
-0,38268343 |
-1,14916 |
|
5 |
11 |
-0,5676 |
1,4887745 |
0,99144486 |
0,25881903 |
-0,9238796 |
-0,84503 |
|
6 |
13 |
-0,1125 |
1,6004878 |
0,99144486 |
-0,25881903 |
-0,9238796 |
-0,18005 |
|
7 |
15 |
0,2613 |
1,7205837 |
0,92397955 |
-0,707107 |
-0,38268343 |
0,44959 |
|
8 |
17 |
0,5613 |
1,8496913 |
0,793353337 |
-0,965926 |
0,38268343 |
1,03823 |
|
9 |
19 |
0,2803 |
1,9884867 |
0,60876152 |
0,965926 |
0,9238796 |
0,55737 |
|
10 |
21 |
0,1622 |
2,1376969 |
0,32268346 |
-0,707107 |
0,9238796 |
0,34673 |
|
11 |
23 |
0,0932 |
2,298134 |
0,13052629 |
-0,25881903 |
0,38268343 |
0,21419 |
|
12 |
25 |
0,0794 |
2,4705464 |
-0,13052629 |
0,25881903 |
-0,38268343 |
0,19616 |
|
13 |
27 |
0,0769 |
2,655929 |
-0,3226846 |
0,707107 |
-0,9238796 |
0,20424 |
|
14 |
29 |
0,0675 |
2,8552222 |
-0,60876152 |
0,965926 |
-0,9238796 |
0,19273 |
|
15 |
31 |
0,0409 |
3,0694697 |
-0,793353337 |
0,965926 |
-0,38268343 |
0,12554 |
|
16 |
33 |
0,0057 |
3,2997938 |
-0,92397955 |
0,707107 |
0,38268343 |
0,01881 |
|
17 |
35 |
-0,0284 |
3,5474007 |
-0,99144486 |
0,25881903 |
0,9238796 |
-0,10075 |
|
18 |
37 |
-0,0332 |
3,8135873 |
-0,99144486 |
-0,25881903 |
0,9238796 |
-0,12661 |
|
19 |
39 |
-0,0156 |
4,0997478 |
-0,92397955 |
-0,707107 |
0,38268343 |
-0,06396 |
|
20 |
41 |
0,0315 |
4,4073809 |
-0,793353337 |
-0,965926 |
-0,38268343 |
-0,13883 |
|
21 |
43 |
0,0772 |
4,7380979 |
-0,60876152 |
-0,965926 |
-0,9238796 |
0,36578 |
|
22 |
45 |
0,0970 |
5,093631 |
-0,3226846 |
-0,707107 |
-0,9238796 |
0,49408 |
|
23 |
47 |
0,0717 |
5,4758422 |
-0,13052629 |
-0,25881903 |
-0,38268343 |
0,39262 |
|
24 |
49 |
0,0057 |
5,8867335 |
0,13052629 |
0,25881903 |
0,38268343 |
0,03355 |
По формуле Симпсона имеем:
Подставляя a0= 0,07933, a1= -0,17080, b1= -0,13193, a2= 0,23027, b2= -0,32187,
a3= 0,30377, b3= 0,02186, получим
Эту аппроксимацию табулируем с помощью следующей таблицы:
|
1 |
-0,1693 |
0,2224 |
0,2813 |
-0,0172 |
-0,0833 |
0,0084 |
1,0368 |
0,3785 |
0,2967 |
|
9 |
-0,0551 |
-0,1628 |
-0,2806 |
-0,1219 |
-0,2276 |
-0,0084 |
1,3849 |
-0,6375 |
-0,8298 |
|
17 |
0,1039 |
-0,0596 |
0,2803 |
-0,1047 |
0,3109 |
0,0084 |
1,8497 |
0,3799 |
0,5613 |
|
25 |
0,1693 |
0,2224 |
-0,2806 |
0,0172 |
0,0833 |
-0,0084 |
2,4705 |
0,0506 |
0,0794 |
|
29 |
0,1355 |
0,0259 |
0,1162 |
0,0803 |
-0,3109 |
-0,2872 |
2,8552 |
0,0315 |
0,0675 |
|
33 |
0,0551 |
-0,1625 |
-0,2806 |
0,1219 |
-0,2276 |
0,0084 |
3,2988 |
0,0533 |
0,0057 |
|
37 |
-0,0223 |
-0.2224 |
-0,1162 |
0.1308 |
0,0833 |
0,0202 |
3.8136 |
-0,0141 |
-0,0332 |
|
45 |
-0,1578 |
0,1628 |
0,1162 |
0,0803 |
0,2276 |
-0,0202 |
5,0936 |
1,0885 |
0,0970 |
Рассмотренный метод аппроксимации с большой эффективностью использовался при выполнении научно-исследовательских работ в соответствии с тематическим планом ВУЗа [1,2].
Литература:
- Гарькина И. А. Математическое и компьютерное моделирование сложных систем / И. А. Гарькина, А. М. Данилов, Э. Р. Домке. — Пенза: ПГУАС, 2011. -296 с.
- Данилов А. М., Гарькина И. А., Гарькин И. Н. Защита от удара и сопровождающей вибрации: экспоненциально-тригонометрическая аппроксимация функций / Региональная архитектура и строительство, № 3(14), 2012 г. С.85–89.