В статье автор исследует на разрешимость задачу типа Коши, в уравнении которой содержатся слагаемые с конформабельной дробной производной.

Ключевые слова: конформабельная дробная производная, задача типа Коши, метод Лагранжа.

Введение

Конформабельные производные являются сравнительно новой формой дробных производных, которые сохраняют важные свойства обычных производных (линейность, цепное правило и др.), что делает их удобными для анализа и моделирования. Такие производные успешно применяются в моделировании процессов с эффектом памяти или наследуемости (в физике, биологии, экономике и инженерии), а задача Коши — это базовая постановка, определяющая начальные условия и развитие процесса.

Пусть функция . Тогда, для всех “конформабельная дробная производная” от функции f определяется в виде [1]:

, (1)

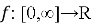
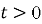
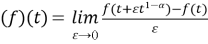
где (0, 1) и является порядком дробной производной.

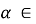
Если у функции f существует конформабельная дробная производная порядка , тогда будем говорить, что f -дифференцируемая.

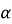
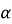
Если функция -дифференцируемая в точке , тогда — непрерывная в точке .

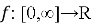
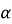
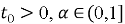
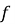
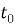
Пусть и функции f, g — дифференцируемые функции при . Тогда справедливы следующие соотношения:

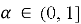
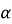
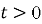
1) (f) + b (g).

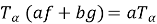
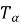
2) ( ) = p .

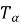
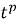
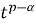
3) ( ) = 0, для всех линейных функций f(t) = .

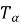
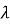
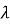
4) (fg) = (f)g + (g)f.

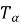
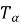
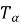
5) ( ) =

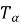
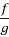
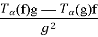
Если f дифференцируемая функция, тогда [2]:

(f)(t) = (t). (3)

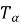
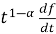
Постановка задачи

В области , требуется найти решение уравнения:

, (4)

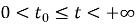
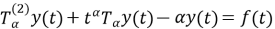
где — непрерывная дифференцируемая (в классическом смысле) функция при . Решение дифференциального уравнения удовлетворяет следующим условиям:

, , (5)

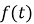
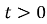
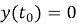
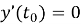
где — порядок производной.

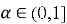
Решение ищем в пространстве функций: , где const .

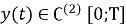
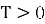
Задачу типа Коши (4)-(5) решаем методом вариации произвольных постоянных [3].

Решение задачи типа Коши (4)-(5)

Используя свойство (3) конформабельной дробной производной, вычислим :

(6)

. (7)

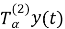
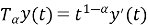
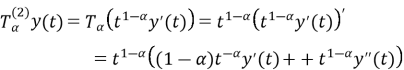
Подставив (6) и (7) в уравнение (4), получим обыкновенное дифференциальное уравнение 2-го порядка:

. (8)

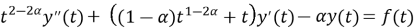
Общее решение однородного уравнения, соответствующего уравнению (8), имеет вид:

. (9)

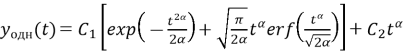
где — функция ошибок.

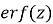
Общее решение неоднородного уравнения ищем методом вариации постоянных, константы и в выражении (9) варьируем, то есть решение неоднородного уравнения ищем в виде:

, (10)

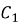
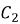
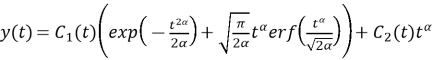
где и — пока неизвестные функции. Следуя методу Лагранжа, найдем и :

,

.

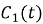
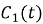
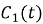
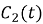
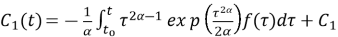
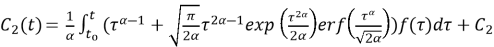
Подставив найденные и в (10), получим общее решение неоднородного дифференциального уравнения 2-го порядка (8):

, (11)

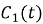
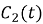
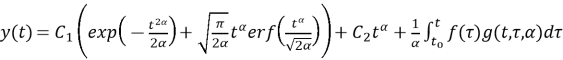
где :

. (12)

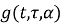
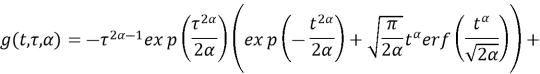
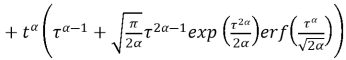
Применив начальные условия (5) к полученному общему решению (12), найдем .

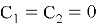
Методом от «противного» можно показать, что полученное решение будет единственным.

Основной результат

Доказана Теорема

Теорема

В области , задача типа Коши:

,

, ,

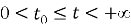
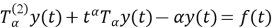
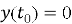
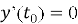
где — непрерывная дифференцируемая (в классическом смысле) функция при , — конформабельная производная порядка

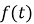
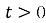
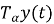
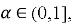
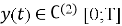
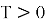
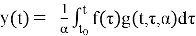
имеет единственное решение в пространстве функций: , где const , определяемое формулой

,

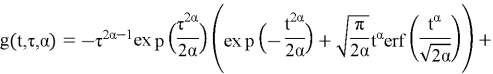
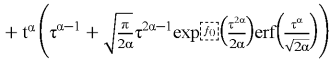
где

,

где — функция ошибок.

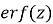
Заключение . Итак, в работе

1. Изучено понятие конформабельной дробной производной.
2. Произведена постановка задачи типа Коши с конформабельной дробной производной в уравнении.
3. Доказана теорема существования и единственности решения поставленной задачи.

В-дальнейшем планируется:

1. Расширить интервал изменения порядка производной
2. Рассмотреть применение конформабельной дробной производной для решения дифференциальных уравнений в частных производных.
3. Исследовать на разрешимость задачу типа Коши, в которой начальные условия содержат конформабельную дробную производную.

Литература:

1. R. Khalil A new definition of fractional derivative// Journal of Computational and Applied Mathematics. — 2014. — 264 (2014) 65–70. — P. 65–70.
2. Thabet Abdeljawad On conformable fractional calculus // Journal of Computational and Applied Mathematics. — 2014. –279(2015)57–66. — P. 58–66.
3. Арнольд В. И. Обыкновенные дифференциальные уравнения. — М.: МЦНМО, 2012.