В данной работе изучается нелинейная обратная задача для линейного уравнения теплопроводности с дробными производными по времени с условиями переопределения во внутренней точке. Сначала изучается прямая задача. С помощью метода Фурье эта прямая задача сводится к эквивалентному интегральному уравнению. Затем с помощью оценок функции Миттаг-Леффлера и некоторых ее свойств обратная задача сводится к эквивалентной системе интегральных уравнений. Для решения этой системы используется метод интегральных уравнений Вольтерра. Доказываются глобальные теоремы существования и единственности решения рассматриваемой обратной задачи.

Ключевые слова: уравнение дробного по времени порядка, дробная производная обратная задача, интегральное уравнение Вольтерра.

In this paper, we study a nonlinear inverse problem for a linear heat conductivity equation with fractional time-diffusion derivatives with overdetermination conditions at an interior point. First, we study the direct problem. Using the Fourier method, this direct problem is reduced to an equivalent integral equation. Then, using estimates of the Mittag-Leffler function and some of its properties, the inverse problem is reduced to an equivalent system of integral equations. To solve this system, the Volterra integral equation method is used. Global theorems of existence and uniqueness of the solution of the inverse problem under consideration are proved.

Keywords: fractional time equation, fractional derivative, inverse problem, integral equation, Volterr.

Введение

Теория дробных дифференциальных уравнений в частных производных в последнее время получила значительное применение в различных областях науки и техники, в частности оно возникает таких как физика, химия, электродинамика сложных сред, реология полимеров и т. д.

В последнее время исследование дробных дифференциальных

уравнений достигло большого прогресса. В литературе существует несколько определений дробных интегралов и производных, наиболее популярные определения — в смысле производных Римана–Лиувилля и Капуто. Прямые задачи для дифференциальных уравнений в частных производных дробного порядка посвящены монорафии [1- 7].

Обратные задачи для целочисленных и дробных уравнений в частных производных — бурно развивающаяся область математики. Если классические постановки краевых задач для этих уравнений уже достаточно хорошо изучены и получены условия их разрешимости, то с обратными задачами дело обстоит сложнее. Зачастую даже сама постановка таких задач требует дополнительных исследований, в том числе и изучения дифференциальных свойств решений прямых задач.

1.Определение дробных проиводных и интегралов.

Введем некоторые понятия, необходимые для дальнейшего исследования.

Определение 1. Дробным дифференциальным оператором Капуто порядка для дифференцируемой функции называется оператор, определенная выражением [3,4]:

(1)

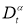
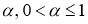
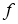
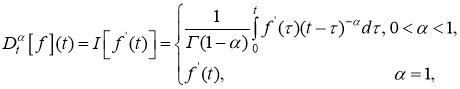
где гамма функция.

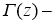
Определение 2. Дробным интегральным оператором Римана-Лиувилля порядка для интегрируемой функции называется оператор, определенная выражением [3,4]:

(2)

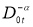
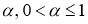
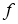
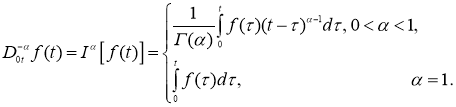
Определение 3. Дву параметрическая функция определяемое формулой [3]:

, (3)

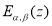
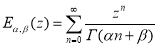
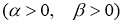
называется функцией Миттаг-Леффлера.

Приведем некоторые соотношения, приведенные в [3]- [6]:

(4)

(5)

(6)

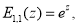
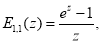
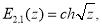
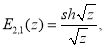
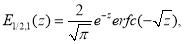
При получим одно параметрическую функцию Миттаг-Леффлера:

. (7)

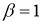
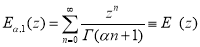
Обобщение формулы Ньютона-Лейбница, при

(8)

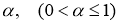
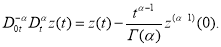
Лемма 1. Если и , то

(9)

(10)

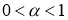
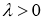
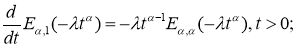
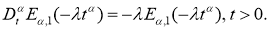
Лемма 2. Если и , то

(11)

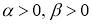
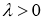
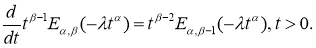
Доказательство этих лемм следует из определения дробной производной Капуто и дифференцирования двухпараметрической функции Миттаг-Леффлера.

Лемма 3 (см. [12]). Если для и функция , то

(12)

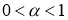
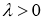
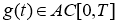
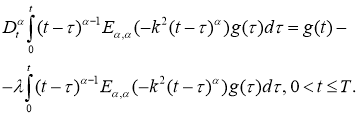
В частности, если , то

(13)

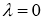
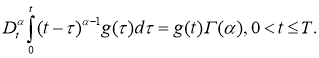
Пусть фиксированнре число.

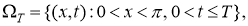
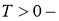
2. Постановка и основной результат. Вобласти рассмотрим первую начально-краевую задачу

. (14)

(15)

(16)

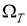
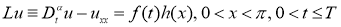
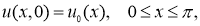
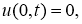
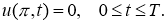
где , заданные функции.

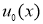
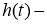
Здесь дробная производная Капуто порядка .

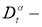
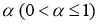
Обратная задача . Требуется найти пару функций из следующих условий

(17)

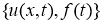
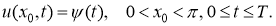
Пусть все заданные функции достаточно гладкие

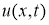
Определение 3. Функция называется классическим решением начально-краевой задачи (14) — (16), если

1) дважды непрерывно диффенцируемая функция в области , т. е. ;

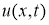
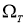
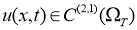
2) удовлетворяет уравнению (14), начальному условию (15) и граничным условиям (16) в классическом смысле.

Определение 4. Пара функций и называется решением обратной задачи (14)-(17), если , и удовлетворяют равенствам (14)-(17) в классическом смысле.

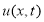
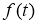
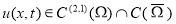
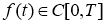
Справедлива

Теорема 1. Пусть , , , ,, и кроме того выполнены условия согласования . Тогда для любого Т>0 решение обратной задачи (14)-(17) на отрезке существует, единственно и принадлежит классу .

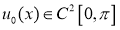
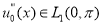
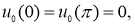
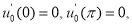
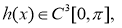
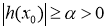
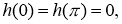
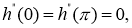
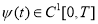
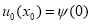
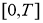
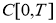
Доказательство. Решение обратной задачи (14)-(17) будем искать в виде

. (18)

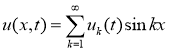
Разложим функции в ряд Фурье

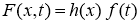
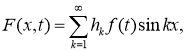
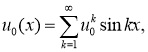
где

(19)

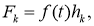
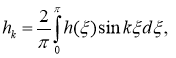
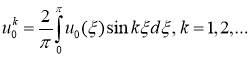
Подставляя (18) и выражения для функции в уравнение (14), получим

(20)

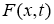
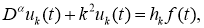
при условии

. (21)

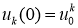
Задача (20), (21) имеет единственное решение и это решение представимо в виде

.

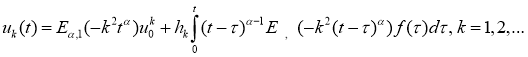
Непосредственно оценивая функцию для и учитывая неравенство (см. [1], с.44–45), получим

,

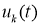
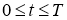
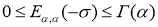
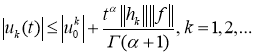
где .

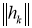
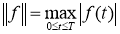
Подставляя выражения для в (18), имеем

(22)

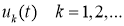
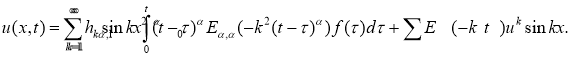
В формуле (16), интегрируя по частям три раза, получим

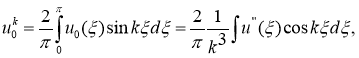
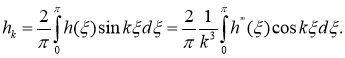
Отсюда, в силу неравенства Бесселя ряды из квадратов и сходятся, поэтому и при . Следовательно, ряд (22) при сходится равномерно и абсолютно. Поэтому функция , определяемая рядом (22), непрерывна в области и удовлетворяет начальному и граничным условиям. Нетрудно показать, что функция удовлетворяет уравнению (14) в области . Для этого достаточно показать равномерную сходимость рядов .

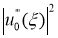
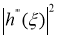
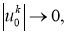
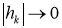
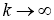
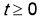
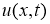
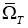
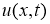
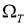
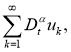
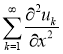
Докажем существование и единственность решение обратной задачи (14)-(17). Пусть является решением обратной задачи (14) -(17). Дифференцируя соотношение (22) оператором и учитывая формулы (10), и используя переопределение (17), находим

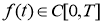
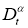
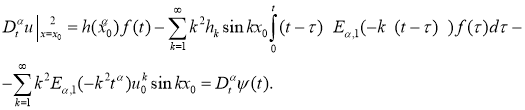
или

(23)

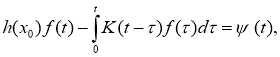
где

.

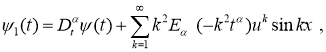
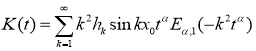
Покажем, что функции являются непрерывными. Это следует из условий наложенных на заданные функции. функции , являются непрерывными,

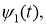
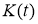
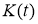
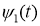
Следовательно, интегральное уравнение (23) является интегральным уравнение Вольтерра второго рода. следовательно, уравнение (23) имеет единственное решение

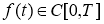
Далее подставляя функцию в (23), однозначно находим функцию . Как и в работе [8], что эта функция является решением обратной задачи (14)-(17). Теорема доказана.

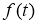
Литература:

1. Kilbas A. A., Srivastava H. M. and Trujillo J. J. “Theory and Applications of Fractional Differential Equations,” North-Holland Mathematics Studies , Vol. 204, 2006.
2. Miller K. S. and. Ross B. “An Introduction to the Fractional Calculus and Fractional Differential Equations,” John Wiley, New York, 1993.
3. Podlubny I. “Fractional Differential Equations,” Aca- demic Press, San Diego, New York, London, 1999.
4. Самко С. Г., Килбас А. А., Маричев О. И. Интегралы и производные дробного порядка, и некоторые их приложения. — Минск: Наука и техника, 1987. — 688 с.
5. Нахушев А. М. Дробное исчисление и его применение. М.: Физматлит, 2003. 272 с.
6. Учайкин В. В. Метод дробных производных. Ульяновск: Артишок, 2008. 512 с.
7. Псху А. В. Уравнения в частных производных дробного порядка. М.: Наука. 2005. 199 с.
8. Аблабеков Б. С. Обратные задачи для псевдопараболических уравнений.- Бишкек: Илим, 2001. –183 с.
9. Денисов А. М. Введение в теорию обратных задач. М.: МГУ, 1994.
10. Тихонов А. Н., Самарский А. А. Уравнения математической физики. М.: Наука, 1966. 724 с.
11. T. Wei and Z. Q. Zhang, Robin coefficient identification for a time-fractional diffusion equation, Inverse Prob. Sci. Eng. 24, 647–666 (2016).