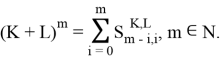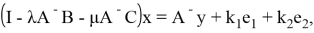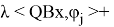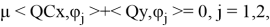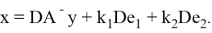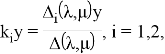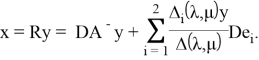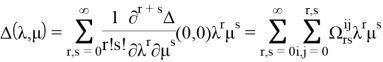Для линейного фредгольмова оператора с нулевым индексом в частном случае двумерного ядра получена формула его (B,C)-резольвенты.
Ключевые слова: линейные операторы, фредгольмов оператор, банахово пространство, резольвента.
- Необходимые сведения
Пусть
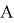
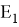
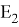
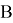
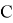
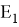
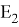
Определение.
Оператор
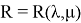
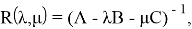
где
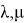
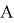
Далее, для краткости, ( B , C )-резольвенту будем называть просто резольвентой.
Вводится проектор
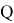
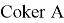
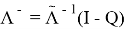
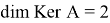
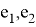
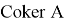
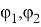
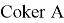
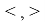
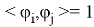
Лемма 1 [2] . Уравнение
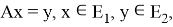
равносильно системе
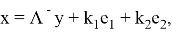
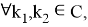
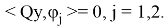
Пусть
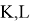
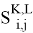
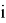
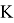
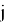
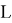
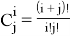
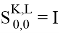
Лемма 2 [3]. Справедлив следующий аналог бинома Ньютона:
|
|
(1) |
Замечание 1.
Вчастности, если
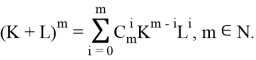
Лемма 3
[4]
.
Пусть
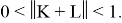
Тогда оператор
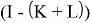
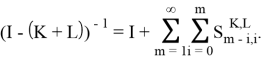
Доказательство. Действительно, как операторная сумма бесконечной геометрической прогрессии, в силу леммы 2, имеем:
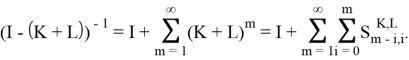
Следующая лемма является обобщением формулы дифференцирования определитель-функции
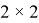
Лемма 4. Пусть
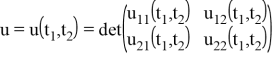
— определитель-функция, где
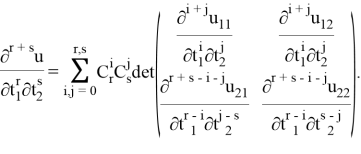
Цель работы: получить аналитическое выражение для
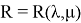
- Вывод формулы ( B , C )-резольвенты
Рассмотрим уравнение
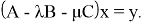
В силу леммы 1 оно равносильно системе
|
|
(2) |
|
|
(3) |
где
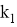
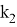
Наложим следующие
Условие 1.
Операторы
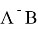
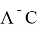
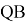
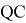
Условие 2.
Числа
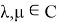
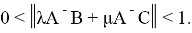
Тогда существует оператор
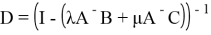
и равенство (2) можно обратить:
|
|
(4) |
Подставив (4) в (3), получим систему для вычисления
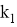
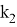
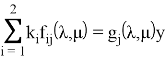
в обозначениях
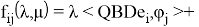
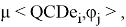
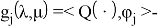
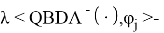
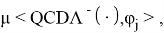
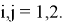
Далее, по формулам Крамера, получим решение системы
|
|
(5) |
в обозначениях
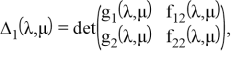
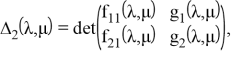
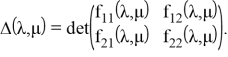
Тогда, подставив (5) в (4), получим искомую формулу для резольвенты
|
|
(6) |
Замечание 2. Всилу условий 1,2 и леммы 3 имеем:
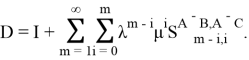
В силу условия 1 и замечания 2 выполнено
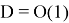
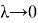
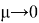
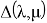
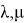
Разложим ее в ряд Маклорена [6] в окрестности точки
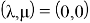
|
|
(7) |
в обозначении
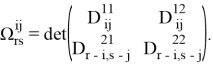
Тем самым, получен следующий результат.
Теорема.
Пусть выполнены условия 1,2. Тогда (B,C)-резольвента линейного Ф-оператора
Литература:
- Усков В. И., Пантелеева А. Г. Исследование задачи Коши для некоторого возмущенного алгебро-дифференциального уравнения первого порядка на явление погранслоя // Молодой ученый. ‒ 2020. ‒ № 25 (315). ‒ С. 84‒87.
- Uskov V. Regularization of an algebro-differential first-order equation with a Fredholm operator in the derivative // Norwegian Journal of development of the International Science. — 2020. — No 38. — PP. 21‒22.
- Усков В. И. Решение задач для уравнений соболевского типа методом каскадной декомпозиции // Дисс… канд. физ.-мат. наук. — Воронеж, 2019. — 137 с.
- Ряд Неймана. https://ru.wikipedia.org/wiki/Ряд_Неймана (дата обращения: 26.07.2020).
- Усков В. И., Анжаурова Т. М. Решение линейных рекуррентных соотношений второго порядка // Молодой ученый. — 2019. — № 42 (280). — C. 1–6.
- Ряд Тейлора. https://ru.wikipedia.org/wiki/Ряд_Тейлора#Связанные_определения (дата обращения: 26.07.2020).