В настоящей работе рассматривается обобщенная модель Фридрихса , действующих в прямом сумме 0 — и 1 — частичных подпространств Фоковского пространства.

Найден явный вид определителя возмущения. Обобщенная модель Фридрихса введена в работе [1], где были изучены ее собственные значения и «резонансы» (особенности аналитического продолжения резольвенты). Такие модели рассмотрены также в ряде других работ, из которых мы упомянем статью [2] — в ней результаты, полученные для обобщенной модели Фридрихса, применяются к проблемам случайного блуждания частицы в случайной среде, работу [3], в которой исследованы так называемые связанные состояния для определенного семейства обобщенных моделей Фридрихса, а также работу [4], где полностью исследован спектр модели и структура ее собственных векторов (как обычных, так и обобщенных) при малых значениях параметра взаимодействия. А в работе [5] оно рассматривается как двухканальная молекулярно-резонансная модель.

Пусть - трехмерный тор, т. е. куб  — с соответствующим отождествлением противоположных граней. Всюду в работе рассматривается как абелева группа, в которой операции сложения и умножения на вещественное число введены как операции сложения и умножения на вещественное число в по модулю , где и - множество вещественных и целых чисел, соответственно. Например, если

,

то

.

Пусть  — одномерное комплексное пространство и  — гильбертово пространство квадратично-интегрируемых (комплекснозначных) функций, определенных на . Символом обозначается прямая сумма пространств и , т. е. . Пространства и называются нольчастичным и одночастичным подпространствами фоковского пространства по , соответственно, где

.

Элементы пространтсва представляются как векторы , где , . Для двух элементов , их скалярное произведение

в естественно определяется через скалярные произведения

.

Рассмотрим обобщенной модели Фридрихса , действующее в гильбертовом пространстве и задающихся как блочно–операторная матрица

,

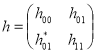где матричные элементы , , определяются равенствами

,

.

При этом  — фиксированное вещественное число, и вещественнозначные непрерывные функции на , а сопряженное оператор к и

.

Здесь и в дальнейшем интеграл без указания пределов всюду означает интегрирование по всей области изменения переменных интегрирования.

Легко можно проверить, что оператор , действующий в гильбертовом пространстве , является ограниченным и самосопряженным.

В математической физике оператор называется оператором уничтожения, а оператор называется оператором рождения. Оператор уничтожения снижает количество частиц в заданном состоянии на единицу, а оператор рождения увеличивает число частиц в данном состоянии на единицу, и является сопряженным к оператору уничтожения. Такие операторы имеют широкое применение в квантовой механике, в частности, в изучении квантовых гармонических осцилляторов и систем многих частиц [6].

Обозначим через , и , соответственно, спектр, существенный спектр и дискретный спектр ограниченного самосопряженного оператора.

Пусть оператор , действует в как

.

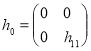Оператор возмущения оператора является самосопряженным оператором ранга 2. Следовательно, из известной теоремы Г. Вейля [7] о сохранении существенного спектра при возмущениях конечнего ранга вытекает, что существенный спектр оператора совпадает с существенным спектром оператора . Известно, что

,

где числа и определяются следующим образом:

.

Из последних фактов следует, что .

Определим регулярную в функцию (детерминант Фредгольма, ассоциированный с оператором )

.

Следующая лемма установит связь между собственными значениями оператора и нулями функции .

Лемма 1. Число является собственным значением оператора тогда и только тогда, когда .

Доказательство. Пусть число  — есть собственное значение оператора и пусть  — соответствующая собственная вектор-функция. Тогда эта вектор-функция удовлетворяет уравнению или системе уравнений

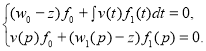(1)

Так как , из второго уравнения системы (1) для имеем

. (2)

Подставляя выражение (2) для в первое уравнение системы (1) заключаем, что система уравнений (1) имеет ненулевое решение тогда и только тогда, когда . Лемма 1 доказана.

Следующая теорема является основным результатом настоящей работы.

Теорема 1.Определитель возмущения оператора относительно оператора имеет вид

.

Доказательство. Так как является оператором ранга 2, определитель возмущения хорошо определена по формуле (см. например [8])

,

где – единичный оператор в . Очевидно, что

.

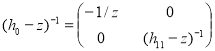Не нарушая общности предположим, что . Выбираем ортонормальный базис следующим образом:

и для любых .

Положим

.

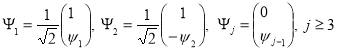По построению система является ортонормальной. Пусть

.

Здесь через обозначен множества натуральных чисел.

С помощью простых вычислений получим

;

;

;

;

в остальных случаях.

Здесь символ Кроникера. Следовательно,

.

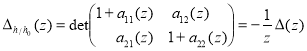Теорема 1 доказана.

Литература:

1.                С. Н. Лакаев. Некоторые спектральные свойства модели Фридрихса. Труды семинара им. И. Г. Петровского, 11 (1986), 210–223.
2.                К. Болдригини, Р. А. Минлос, А. Пеллегринотти. Случайные блуждания в случайной (флуктуирующей) среде. Успехи матем. наук, 62:4 (2007), 27–76.
3.                Е. Л. Лакштанов, Р. А. Минлос. Спектр двухчастичных связанных состояний трансфер-матриц гиббсовских полей (уединенное связанное состояние). Функц. анализ и его прил., 38:3 (2004), 52–69.
4.                Э. Р. Акчурин. О спектральных свойствах обобщенной модели Фридрихса. Теор. и матем. физика, 163:1 (2010), 17–33.
5.                A. K. Motovilov, W. Sandhas, Y. B. Belyaev. Perturbation of a lattice spectral band by a nearby resonance. J. Math. Phys., 42 (2001), 2490–2506.
6.                R. P. Feynman. Statistical mechanics: a set of lectures (2nd ed.). Reading, Massachusetts: Addison-Wesley, 1998, p. 151.
7.                М. Рид, Б. Саймон. Методысовременнойматематическойфизики. Т.4. Анализ операторов. М.: Мир, 1982.
8.                И. Ц. Гохберг, М. Г. Крейн. Введение в теорию линейных несамосопряженных операторов. М.: Наука, 1965.