В статье рассматривается установившаяся фильтрация газов в деформируемом в трещиновато-пористом пласте, в котором проницаемость изменяется экспоненциальной зависимостью от давления.
Ключевые слова: фильтрация, газ, трещиновато-пористый, установившийся, экспоненциальный.
The article considers the steady-state filtration of gases in a fractured-porous formation, in which the permeability changes exponentially depending on the pressure.
Key words: filtration, gas, fractured-porous, steady-state, exponential.
Установившаяся фильтрация газов рассматривается во многих работах [1,2,3]. Но в них 
Рассмотрим установившуюся фильтрацию газов в трещиновато-пористом пласте, взяв изменение проницаемости в пласте экспоненциально в зависимости от давления.
В трещиновато-пористом пласте дебит скважины складывается из дебита газа, протекающего из трещин, и из дебита газа, поступающего из пористых блоков.
В случае сохранения в трещиноватой части зависимости проницаемости от давления имеем:
. (1)
Поскольку при установившемся движении газов расход сохраняется вдоль оси r, то получаем:
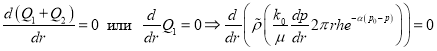
(2)
В уравнении (2) учитывается уравнение состояния:
(3)
Здесь 
– средневзвешенная плотность; 
– средневзвешенное давление.
Разделив обе части уравнения (2) на постоянные величины, получаем:
(4)
Решение уравнения 
при условиях 
известно [1]:
В этом случае распределение давления получается в следующем виде:
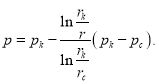(5)
Тогда для дебита 
получаем:
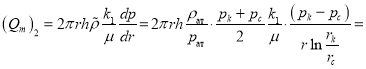
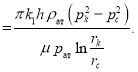(6)
или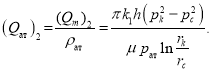 
Теперь решим уравнение для трещиноватой части:
(7)
Уравнение (7) с учетом (3) и после деления обеих частей уравнения на постоянные величины можно написать в следующем виде:
(8)
Получаем:
При 
(9)
При 
(10)
Вычитая из уравнения (10) уравнение (9), получаем:
откуда
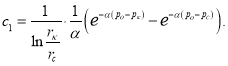(11)
Подставляя (11) в (9), получаем:
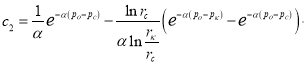(12)
Подставляя (11) и (12) в 
, получаем:
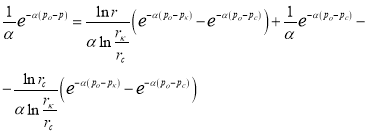
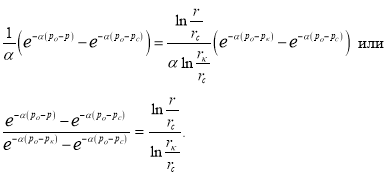
При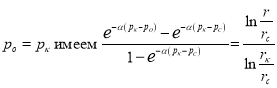 
или 
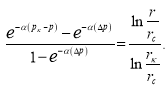(13)
Как видим, распределение давления имеет следующий вид:
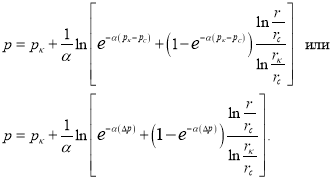(14)
Тогда для дебита после несложных преобразований, получаем:
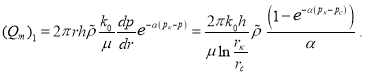(15)
Учитывая (8) в (15) мы получаем:
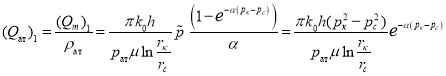(16)
При 
мы получаем формулу для установившейся фильтрации газа в пористой среде: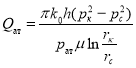 
(17) Таким образом, в статье получена формула для установившейся фильтрации газа в трещиновато-пористом пласте в виде:
= 
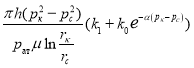(18)
Литература:
- Басниев К. С. Нефтегазовая гидромеханика /К. С. Басниев, Н. М. Дмитриев, Г. Д. Розенберг. — Москва-Ижевск: Институт компьютерных исследований, 2005.
- А. Х. Мирзаджанзаде, А. Г. Ковалев, Ю. В. Зайцев. Особенности эксплуатации месторождений аномальных нефтей. –М.: Недра, 1972, с.200.
- А. Т. Горбунов. Разработка аномальных месторождений. — М.: Недра, 1981, 240 с.
