В настоящее время разработка методов и алгоритмов ручного и автоматического управления БПЛА является интенсивно развивающимся направлением научных исследований в военной, гражданской и космической области. При использовании мультикоптеров одна из самых актуальных задач, это задача автоматической заправки аккумуляторов, а, следовательно, задача точной посадки в выбранную точку или ограниченный участок.
Посадка — это обязательный этап применения любого БПЛА, независимо от его функционального назначения. Поэтому поиск и разработка новых способов, схем и средств посадки БЛА является одной из наиболее актуальных задач [1].
Ключевые слова: беспилотные летательные аппараты, ошибка оценивания, уравнения состоянии, уравнения наблюдения, фильтр Калмана, расширенный фильтр Калмана.
Постановка задачи: Имеется мини-БПЛА (мультикоптер), посадочная площадка с 4-мя маяками. Предполагаем, что выход БПЛА в зону маяков будет осуществлен с использованием системы GPS и/или ГЛОНАСС. Требуется разработать алгоритм точного выхода мультикоптера в заданную точку и его посадки.
Для оценки и сглаживания текущих координат летящего мультикоптера будет использован алгоритм фильтрации Калмана.
Фильтр Калмана это рекурсивный фильтр, который минимизирует среднеквадратическую ошибку оценивания текущих координат объекта.
Суть алгоритма оценивания заключается в последовательном предсказании искомых координат мультикоптера с использованием модели состояний с последующей коррекцией результатов по данным фактических измерений.
Модель движения БПЛА рассматривается как движение материальной точки с ограничениями, накладываемыми на скорость и ускорение движения, а также на изменение ускорения.
При синтезе алгоритма оценивания параметры заданы с помощью системы разностных уравнений первого порядка, в общем случае нелинейной.
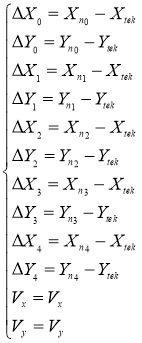(1)
Где 
– известные заранее координаты маяков 
, (i=0,1,2,3,4 — номера маяков); 
— текущие координаты мультикоптера; 
— приращение расстояний между мультикоптером и маяками; 
— ортогональные составляющие скорости движения мультикоптера; 
— дальность от маяка i до мультикоптера.
Введем вектор состояний, включающий неизвестные и подлежащие оцениванию переменные системы (1)
или 
(2)
В разностной форме система уравнений (1) с учетом (2) приобретает следующий вид
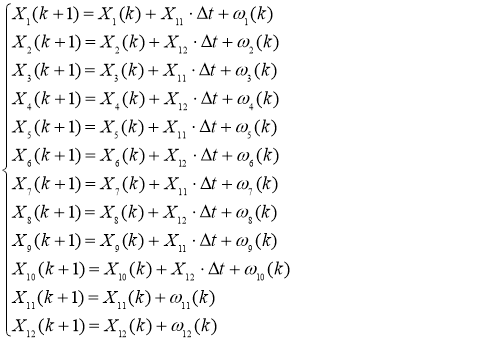(3)
где k — дискретное текущее время с интервалом дискретизации 
; 
- вектор состояний, вектор-столбец размерностью (12x1) и включает в себя неизвестные и подлежащие оцениванию параметры динамической системы; 
– вектор шумов состояний размерностью (12x1).
Уравнения наблюдения, учитывающие функциональные связи между выбранным вектором состояния и измерительными каналами запишем в виде:
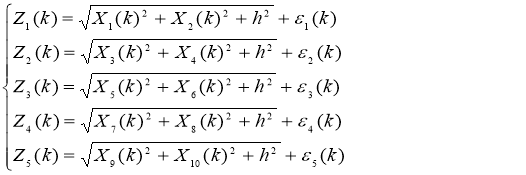(4)
- вектор фактических измерений размерностью (5x1); h — высота полета мультикоптера над Землей; 
— вектор шума измерений.
Как правило, шумы, входящие в модели состояний и наблюдений, считаются белыми гауссовыми шумами
Задача оценивания значений переменных состояния системы (2) сводится к синтезу некоторого алгоритма, обеспечивающего эту оценку по текущим измерениям Z(k) с минимальными ошибками. Ошибка оценивания может быть определена следующим образом:
(5)
Здесь 
— оценка вектора состояния в момент времени k, 
- ошибка оценивания вектора состояния 
.
Для нелинейной системы уравнений наблюдений (4) в терминах расширенного фильтра Калмана оценка дальностей на шаге (k+1) вычисляется:
,
где 
- оценка вектора состояния на момент времени (k+1); 
- вектор предсказанных оценок на момент времени (k+1) по данным на шаге k; 
- матрица весовых коэффициентов; 
— матричное уравнение для расчета вектора предсказания;
Поскольку уравнения наблюдений являются нелинейными функциями вектора наблюдения, то применяют методы аппроксимации нелинейных выражений с помощью разложения в ряд Тейлора вблизи оптимальной оценки.
Такой подход применен в расширенном фильтре Калмана, тогда расчет весовых коэффициентов осуществляется по рекуррентным матричным уравнениям следующего вида:
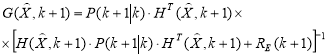(6)
(7)
(8)
Структурная схема расширенного фильтра Калмана приведена на рис. 1.
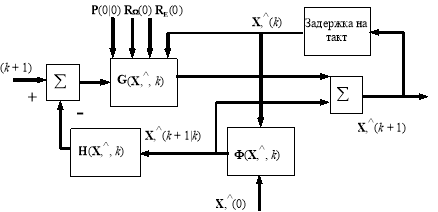
Рис. 1. Структурная схема расширенного фильтра Калмана
Для инициации работы алгоритма необходимо задать начальные значения матрицы ковариации ошибок оценивания 
, начальный вектор оценок 
и диагональные элементы корреляционных матриц ошибок наблюдения 
и состояния 
.
Начальные значения вектора 
могут быть заданы как средние величины исходя из предполагаемых максимальных и минимальных значений. Априорная корреляционная матрица ошибок оценивания является диагональной. Значения диагональных элементов соответствуют дисперсиям ошибок оценивания в начальный момент времени [2,3].
Заключение: В работе выполнен синтез алгоритма посадки беспилотного летательного аппарата в декартовой системе координат с использованием каналов измерения GPS/ГЛОНАСС
Получен пример работы модели в среде Matlab
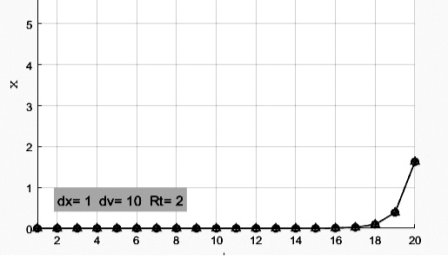
Рис. 2. Процесс изменения координаты и его оценки
Литература:
- Агеев А. М., Михайленко С. Б., Зезюля В.А Способ точной посадки беспилотного летательного аппарата // Сборник статей и докладов по материалам ежегодной научно-практической конференции «Перспективы развития и применения комплексов с беспилотными летательными аппаратами» г. Коломна, 2016. — с.16.
- Сейдж Э. Теория оценивания и ее применение в связи и управлении / Э. П. Сейдж, Дж.Л. Мелс. — М.: Связь, 1976. — 496 с.
- Попов Ю. Б. Алгоритм определения местоположения подвижного источника излучения в двухпозиционной угломерной динамической системе / Ю. Б. Попов, В. А. Кураков, К. Ю. Хабарова // Автометрия. — 2005. — № 4(41). — С. 70–77.
