Для интегро-дифференциальных уравнений
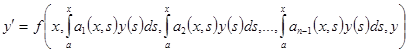 (1)
(1)
изучается задача с функциональным условием:
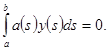 (2)
(2)
Предполагается, что функции 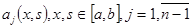 дифференцируемы и для них выполнены условия
дифференцируемы и для них выполнены условия
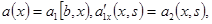
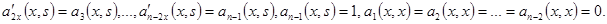
Делается замена
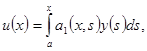 (3)
(3)
из которой последовательным дифференцированием получаем
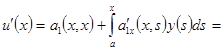
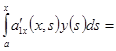
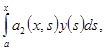
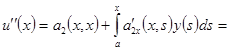
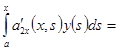
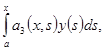
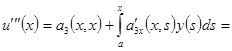
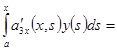
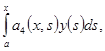
_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _
_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _
_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _
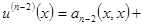
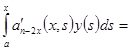
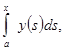
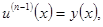
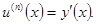
Тогда уравнение (1) с функциональным условием (2) приводится к дифференциальному уравнению 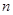 - порядка
- порядка
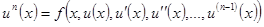 (4)
(4)
с граничными условиями
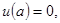
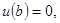
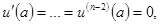 (5)
(5)
т.е. получится двухточечная краевая задача (4), (5), как частный случай задачи Валле-Пуссена, которая изучена во многих работах 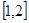 . Если в (2) положить
. Если в (2) положить 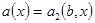 или
или 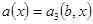 и т.д.
и т.д. 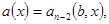 то в место условий (5) получаются различные вариации других граничных условий в точках
то в место условий (5) получаются различные вариации других граничных условий в точках 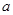 и
и 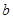 , также являющиеся частными случаями задачи Валле-Пуссена.
, также являющиеся частными случаями задачи Валле-Пуссена.
Из метода получения для задачи (1), (2) задачи (4), (5) следует, что и задачу (4), (5) используя замену (2) можно свести к функциональной задаче (1), (2) или к ее разновидностям. Поэтому можно считать, что доказана следующая
Т е о р е м а. Для разрешимости функциональной задачи (1), (2) при выше приведенных ограничениях для функции 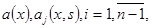 необходимо и достаточно, чтобы была разрешима задача (4), (5).
необходимо и достаточно, чтобы была разрешима задача (4), (5).
Предложенную идею можно использовать и при получении условий разрешимости интегро-дифференциального уравнения вида
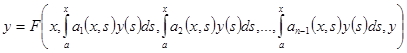
и некоторых интегро-дифференциально-алгебраических уравнений с различными граничными условиями 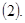
Литература:
1. Исраилов С.В., Юшаев С.С. Многоточечные и функциональные краевые задачи для обыкновенных дифференциальных уравнений. Нальчик.: «Эль-Фа». 2004. С.440.
2. Исраилов С.В., Юшаев С.С. Преобразование одних краевых задач для ОДУ в другие. // Функционально-дифференциальные уравнения и их приложения. Тезисы третьей Международной научной конференции. Махачкала. 2007. С. 45-47.

