Статья направлена на изучение одного из фундаментальных понятий теории вероятностей — нормального распределения и его эмпирическую проверку посредством эксперимента с использованием классического устройства — доски Гальтона.

Актуальность обусловлена значением, которое нормальное распределение играет в статистике и смежных дисциплинах. Изучение закономерностей распределения частиц при случайных взаимодействиях позволяет глубже понять принципы статистической механики, моделирования случайных процессов и прогнозирования исходов в условиях неопределённости. Полученные знания находят применение в физике, биологии, экономике, социологии и других областях, где важна работа с вероятностными моделями.

Еще в древности люди заметили, что за кажущейся случайностью отдельных событий скрываются определённые закономерности. Например, было замечено, что вероятность успешного попадания копья в цель, такую как зубр, значительно возрастает при коллективной охоте по сравнению с индивидуальными действиями. Со временем возникла потребность в более строгой классификации случайных событий: выделялись невозможные, достоверные, маловероятные и высоковероятные исходы.

Одним из первых примеров системного наблюдения за случайными явлениями можно считать опыт с подбрасыванием монеты. При единичном броске невозможно точно предсказать, выпадет ли герб или решка. Однако при многократном повторении эксперимента становится очевидным, что частота выпадения герба приближается к 50 %.

Этот принцип был подтверждён рядом экспериментальных исследований. В XVIII веке французский учёный Жордан Бюффон провёл серию из 4040 бросков, в результате которой герб выпал 2048 раз. В XX веке английский математик Карл Пирсон увеличил объём испытаний до 24 000 бросков монеты, зафиксировав 12 012 выпадений герба. Его результаты также подтвердили устойчивость относительной частоты около теоретического значения 0.5.

Подобные опыты неоднократно воспроизводились другими исследователями, демонстрируя стабильность статистических характеристик случайных процессов. Таким образом, даже при отсутствии детерминированности в отдельно взятом событии, на уровне множества повторений проявляется устойчивая тенденция — эмпирическая основа для понимания вероятностных моделей.

Согласно литературным источникам, доска Гальтона (или квинтильное устройство) была предложена английским учёным Фрэнсисом Гальтоном в конце XIX века и с тех пор активно используется в статистике и физике как инструмент визуализации случайных процессов и формирования нормального распределения [1]. Основными конструктивными элементами устройства являются вертикальная панель с равномерно расположенными препятствиями, отверстие для загрузки шариков сверху и система приёмных лотков в нижней части устройства, позволяющая зафиксировать результаты их падения.

Особую значимость в функционировании доски Гальтона представляет вероятностный характер траекторий шариков, обусловленный множеством случайных факторов. На каждом этапе взаимодействия шарика с препятствием возникает неопределённость направления его дальнейшего движения — он может отклониться как влево, так и вправо с определённой вероятностью.

Эта случайность обусловлена рядом физических факторов, включая микронеровности поверхности препятствий, неоднородность распределения массы шарика, локальные воздушные потоки вблизи конструкции, анизотропию физико-механических свойств материалов (например, коэффициент трения и упругости поверхностей).

Анализ указанных факторов позволяет рассматривать доску Гальтона как эффективную модель случайных процессов, находящую применение в статистической физике, теории вероятностей и моделировании биномиального и нормального распределений. Её наглядность и простота делают её удобным инструментом для демонстрации принципов вероятностного поведения частиц в условиях ограниченной детерминированности.

Для наглядной демонстрации нормального распределения было принято решение о самостоятельной сборке устройства. В качестве основных материалов были выбраны деревянная плита, оргстекло и деревянные штырьки, обеспечившие как функциональность, так и визуальную доступность процесса.

Рис. 1

В верхней части доски находится отверстие, через которое с помощью воронки сбрасывают шарики. При рассмотрении движение отдельных шариков можно увидим, что при одинаковых начальных условиях их траектории различаются, и они попадают в разные ячейки. Однако, если сбросить большое количество шариков малыми партиями, их распределение по ячейкам будет следовать определенным закономерностям: большинство шариков соберется в средней (нулевой) ячейке, а чем дальше ячейка отстоит от нуля, тем меньше шариков туда попадает.

Несмотря на недостатки установки и наблюдающиеся отклонения от нормального закона флуктуаций, результат получается достаточно наглядным.

В экспериментальной части шарики засыпались так, чтобы заполнить центральную ячейку доверху. Задача состояла в построении ступенчатой диаграммы (гистограммы), пример которой представлен на рисунке 2 для идеального случая, а затем в построении графика функции распределения f(x) _эксп . Далее нужно сравнить полученный график с теоретическими данными, чтобы найти значение σ _эксп и записать аналитический вид экспериментальной функции распределения.

Система координат начинается в центре доски Гальтона. В рамках работы выполнено 20 измерений. Средние значения экспериментов сведены в таблицу 1.

Таблица 1

Экспериментальные результаты

В крайних результатах слева и справа таблицы, выделенные жирным шрифтом, не являются экспериментально измеренными, поскольку в данные карманы шарики либо не попали, либо попало настолько мало, что экспериментальное значение практически не отличается от нуля. Однако, поскольку мы в дальнейшем будем логарифмировать полученную функцию, то поэтому мы задаем малое значение, отличное от нуля. В данном случае выбрано значение в 120 раз меньше максимально возможного значения, которое равно цене деления линейки, с помощью которой мы измеряем высоту карманов.

Гистограмма, построенная по результатам таблицы, представлена на рис. 2.

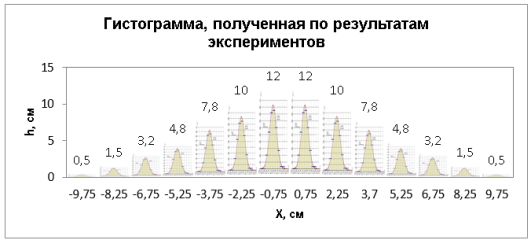
Рис. 2. Гистограмма, полученная по результатам эксперимента. Значения x, приведенные по оси абсцисс приближенно равны координатам центров карманов

Известно, что распределение Гаусса для математического ожидания х ₀ =0 и среднеквадратичного отклонения  описывается математической формулой.

F(х) = (1)

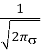
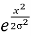
Если мы прологарифмируем и примем z  x ² , то получим линейную функцию

y=LnF(x)=Ln( )-x /22 =kz b (2)

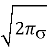
где k  1 / 2 ² , b  Ln  √2. Поскольку карманы расположены симметрично, то получаем две прямых функции: для левой и правой части гистограммы, представленные в таблицах 2 и 3 соответственно.

Таблица 2

Данные для прямой для левой части гистограммы

Таблица 3

Данные для прямой для правой части гистограммы

Исследуя каждую часть по методу наименьших квадратов, найдем константы k и b:

Для левой части получаем k _лев  -0,0962; b  2,63

Для правой части получаем k _прав -0,0957; b  2,66

Видно, что константа k для правой и левой части отличается на 0,5 %, а константа b отличается на 1 %.

Поэтому можно воспользоваться средними значениями данных констант

k  -0,09595, b  2,645

Из формул (2) и (3) видно, что среднеквадратичное отклонение  можно найти тремя способами:

— через максимальное значение гистограммы A max  12 см

=

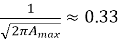
— через значение константы b

=

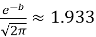
— через значение константы k

=

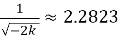
Среди всех рассчитанных значений σ, последним подходящим вариантом для среднеквадратичного отклонения является последнее из трех. Алгоритмы расчёта σ по амплитуде и по константе b также дают слегка заниженные значения среднеквадратичного отклонения, но они также приемлемы для расчетов. Это объясняется тем, что гистограмма, изображённая на рис. 3, немного отличается от нормальной кривой (гауссовы распределения). Построение функции Гаусса вида F = с помощью последнего  =2,2823 см показано на рис. 3

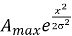
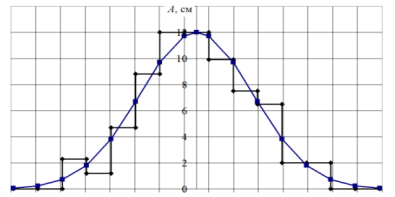
Рис. 3. Нормальное распределение, построенное по результатам экспериментальных измерений

Выводы

Установлено, что установка, применяемая в исследовании, подходит для изучения нормального распределения Гаусса, так как полученное распределение не отличается от гауссова. Результаты исследования демонстрируют практическое проявление закона больших чисел и центральной предельной теоремы, показывая, как случайные отклонения в совокупности формируют устойчивую статистическую закономерность. Нормальное распределение, благодаря своей универсальности, остаётся мощным инструментом анализа и прогнозирования, который может быть полезен даже в случае исходных данных, им не соответствующих, при условии их корректного преобразования.

Литература:

1. Белугин В. И., Величко Т. В., Поповский Э. Е. «Высшая математика», часть 4, методичка УрГУПС, 2001, стр. 29;
2. Белько И. В., Свирид Г. П. «Теория вероятностей и математическая статистика», 2004, стр. 146, 155, 239;
3. Владимиров Д. А., Чебодаев М. И. Краткая теория обработки результатов измерений. Электронные указания по проведению учебного эксперимента. Кызыл. http://nb.tuvsu.ru/content/kratkaya-teoriya-obrabotki-rezultatov-fizicheskih-izmereniy
4. Вентцель Е. С. Теория вероятностей. — 10-е изд., стер.— М., Academia, 2005. — 576 с. — ISBN 5–7695–2311–5. 3. Линник Ю. В. Метод наименьших квадратов и основы математико-статистической теории обработки наблюдений. — 2-е изд. — М., 1962.
5. Ниворожкина Л. И., Морозова З. А. «Математическая статистика с элементами теории вероятностей в задачах с решениями», 2005, стр. 284...287, стр. 585;
6. Письменный Д. Т. «Конспект лекций по теории вероятностей и математической статистике», 2004, стр. 212, 216;
7. Кремер Н. Ш. «Теория вероятностей и математическая статистика», 2006, стр. 173 (формула плотности вероятности  ² — распределения).