Ключевые слова: метод, способ, текстовые задачи.

Обучение решению текстовых задач является сложным и многогранным процессом, требующим от учителя терпения, творческого подхода и постоянного совершенствования методики. Успешное овладение навыками решения текстовых задач не только способствует развитию математических способностей учащихся, но и формирует у них важные жизненные компетенции.

Для эффективного обучения решению текстовых задач в 5–6 классах необходимо использовать различные методы и приемы.

В своей классификации методов Л. П. Стойлова выделяет арифметический, алгебраический, графический и практический методы [1, с.164].

Решить задачу арифметическим методом — это значит найти ответ на требование задачи посредством выполнения арифметических действий над числами. Одну и ту же задачу можно решить различными арифметическими способами. Они отличаются друг от друга математическими моделями.

Задача 1. Сшили 3 платья, расходуя на каждое по 4 м ткани. Сколько кофт можно было сшить из этой ткани, если расходовать на одну кофту 2 м? Решить двумя способами.

Решение: I способ.

1. 4 ⋅ 3 = 12 (м) было ткани;
2. 12: 2 = 6 (кофт) можно сшить из 12 м ткани.

II способ.

1. 4: 2 = 2 (раза) во столько раз больше ткани идет на платье, чем на кофту;
2. 3 ⋅ 2 = 6 (кофт) можно сшить.

Решить задачу алгебраическим методом — это значит найти ответ на требование задачи, составив и решив уравнение или систему уравнений. Если для одной и той же задачи можно составить различные уравнения (системы уравнений), то это означает, что данную задачу можно решить различными алгебраическими способами.

Решение задачи 1 алгебраическим способом:

Обозначим через х шт. количество кофт, которые можно сшить из ткани, которая пошла на платья. Так как на каждую кофту можно расходовать 2 м, то ткани требуется 2х метров, и это столько, сколько израсходовано на 3 платья по 4 метра каждое, т. е. 4 ⋅ 3 (м). Получаем уравнение 2х = 4 ⋅ 3, х = 6, т. е. из 12 м ткани можно сшить 6 кофт, расходуя на каждую 2 м.

Метод математического моделирования, как метод решения текстовых задач выделяли в своих работах Е. И. Лященко [8], Ф. А. Орехов [9], Д.Пойа [10], А. А. Столяр [11], Л. М. Фридман [12].

Метод математического моделирования заключается в описании явлений и процессов реального мира с помощью математических символов. Математическое моделирование осуществляет связь математики с ее приложениями через математические модели, хорошо известные школьникам: уравнения, неравенства, системы уравнений или неравенств [7].

Задача 2. В двух ящиках 120 яблок, причем во второй в 3 раза больше, чем в первой. Сколько яблок в каждом ящике?

Решение:

1. Составим математическую модель. Для этого обозначим за х — количество яблок в первом ящике, тогда количество яблок во втором ящике будет 3х.
2. Составим уравнение: х + 3х = 120.
3. Решим полученное уравнение:

4х = 120,

х = 30

Значит, 3х = 3 ∙ 30 = 90

4. Записываем ответ: 30 яблок в первом и 90 яблок во втором ящиках.

Использовать способ решения наглядного представления условия задачи в виде рисунка или чертежа — значит решить задачу графическим методом [14].

Задача 3. От одной станции одновременно в разных направлениях отошли два поезда. Скорость одного из них 58 км/ч, а другого — 42 км/ч. Через какое время расстояние между поездами будет 1400 км?

Решение: Изобразим движение поездов графически

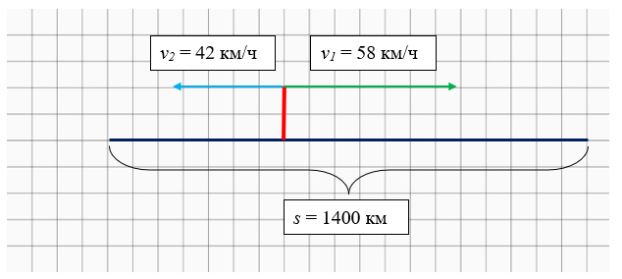
Рис. 1. Движение поездов в разных направлениях

Чтобы найти время, за которое оба поезда проехали данное расстояние, нужно найти общую скорость движения: v _{общ =} v ₁ + v ₂ . Используя формулу пути s = vt, выразим время t = .

Составим выражение: 1400: (58 + 42) = 14 (ч).

Ответ: расстояние между поездами будет 1400 км через 14 ч.

В своих работах Т. В. Захарова, А. И. Пеленков, Е. Н. Яковлева, Т. В. Качурина, Т. В. Котова выделяют арифметический, алгебраический, геометрический, логический, практический методы [2, с.6].

Решить задачу геометрическим методом — значит найти ответ на требование задачи, используя геометрические построения или свойства геометрических фигур. Одну и ту же задачу можно также решить различными геометрическими способами, если для ее решения используются различные построения или свойства фигур [5].

Задача 3. Дачный участок прямоугольной формы требуется огородить забором. Найдите длину забора, если участок имеет размер 45 × 30 м.

Рассмотрим решение задачи 3 геометрическим способом. Для этого построим прямоугольник и обозначим его стороны.

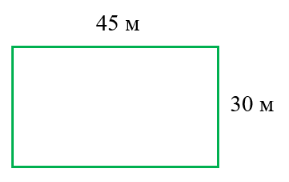
Рис. 2. Дачный участок

Чтобы найти длину забора, надо вычислить периметр прямоугольника по формуле P = (a+b)∙2, значит (45 + 30) ∙2 = 150 (м) — длина забора.

Ответ: 150 м.

Решить задачу логическим методом — это значит найти ответ на требование задачи, как правило, не выполняя вычислений, а только используя логические рассуждения.

Задача 4. Три брата разделили между собой 24 яблока так, что каждый из них получил столько яблок, сколько ему лет. Младший брат, который был недоволен результатом, так как получил меньше всех, предложил: «Я оставлю себе только половину своих яблок, остальные разделю между вами. После меня пусть сначала средний, а потом и старший братья сделают так же, как я. Братья согласились, и яблок, в конце концов, стало у всех поровну. Сколько лет было каждому брату?

Таблица 1

Распределение яблок

Ответ: младшему брату было 4 года, среднему-7, старшему-13 лет.

Решить задачу практическим методом — значит найти ответ на требование задачи, выполнив практические действия с предметами или их копиями (моделями, макетами и т. п.) [5].

Практическим способом учащиеся могут решить задачу, приведенную ниже, не имея никакого представления o дроби и действиях с обыкновенными дробями, а только опираясь на свой жизненный опыт.

Задача 5. Торт разрезали на 8 равных кусков (долей) (Рис. 3). На стол подали 3 доли торта, а потом по просьбе детей принесли еще 2 доли торта (Рис. 4). Сколько долей торта оказалось на столе?

На столе оказалось 5 долей торта, т. е. торта, так как + = = .

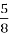
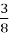
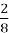
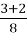
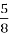
В методическом пособии Н. Б. Истоминой выделены следующие методы решения задач: практический, логический, геометрический, схематический, табличный, арифметический, алгебраический, комбинированный, метод проб и ошибок [6].

Решить задачу схематическим способом — это значит найти ответ на требование задачи, как правило, с помощью схем.

Задача 6. В первый день вскопали всего огорода, а во второй день — всего огорода. Какую часть огорода вскопали за 2 дня? (Матем, ч.2, 5 кл., с.31)

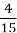
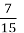
Решение. Нарисуем отрезок, длиной в 15 клеток — это будет весь огород (одна клетка — ).

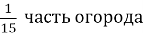
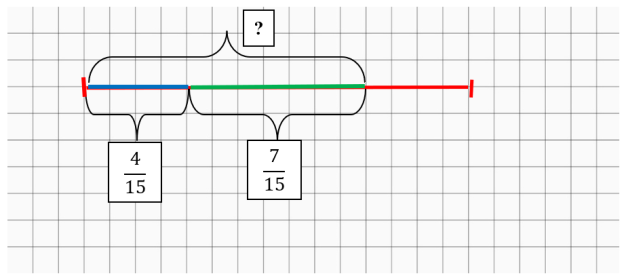
Рис. 5. Схема огорода

+ = вскопали за 2 дня.

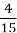
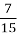
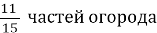
Табличный метод решения задач — это способ структурированного представления информации, где каждый элемент или объект описан в соответствующей ячейке таблицы.

Суть метода заключается в том, что для решения задачи составляется таблица типовой структуры, в которую заносятся значения всех заданных и искомых величин, фигурирующих в условии задачи. Затем по определённому алгоритму устанавливается взаимосвязь между отдельными ячейками таблицы, в том числе с искомыми величинами.

Задача 7. У Саши в коллекции 8 жуков и пауков. У всех насекомых 54 ноги. У одного жука 6 ног, а у одного паука 8 ног. Сколько жуков и сколько пауков у Саши в коллекции?

Таблица 2

Количество ног жуков и пауков

Ответ: у Саши в коллекции 5 жуков и 3 паука.

Метод проб и ошибок заключается в том, что ответ на вопрос задачи угадывается, поэтому он считается самым простым и примитивным.

Задача 8. Площадь прямоугольника равна 180 см², его ширина на 8 см меньше длины. Найти длину и ширину этого прямоугольника.

Решение.Построим математическую модель задачи: x · (x — 8) = 180.

Подбираем решение «экспериментально», методом проб и ошибок.

Найдем значение x, такие, что значение выражения x · ( x — 8) равно 180. По смыслу задачи x > 8.Пусть x = 9, то 9 · (9–8) ≠ 180.

Но 9 слишком маленькое число.Возьмем x =17, то 17· (17–8) ≠ 180, x = 18, то 18 · (18–8) =180 x = 19, то 19 · (19–8) ≠ 180. Итак, если x = 18, то x — 8 = 10.

Ответ: длина 18 см, ширина 10 см.

Иногда в ходе решения задачи применяются несколько методов: алгебраический и арифметический; геометрический и практический и т. п. В этом случае считается, что задача решается комбинированным (смешанным) методом. Комбинированный метод позволяет получить ответ на требование задачи более простым путем.

Задача 9. Из двух городов А и В, расстояние между которыми 250 км, навстречу друг другу выехали два туриста. Скорость движения первого равна 20 км/ч, второго — 30 км/ч. Через сколько часов туристы встретятся?

Например, задачу на движение навстречу друг другу (встречное движение) можно решить комбинированным способом.

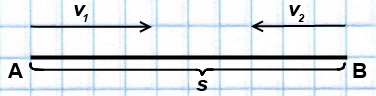
Рис. 6. Схема движения туристов

Чтобы найти скорость сближения двух объектов, движущихся навстречу друг другу, надо сложить их скорости (скорость сближения больше, чем скорость каждого из них).

Таблица 3

Задача на движение

1. 20 + 30 = 50 (км/ч) скорость сближения
2. 250: 50 = 5 (ч) через столько они встретятся.

Ответ: через 5 ч туристы встретятся.

Таким образом, существует широкий спектр методов и подходов к решению текстовых задач, каждый из которых обладает своими преимуществами и ограничениями. Выбор конкретного метода зависит от типа задачи, ее сложности. Решение текстовых задач является важным навыком, который пригодится не только в изучении математики, но и в повседневной жизни. Овладение различными методами решения текстовых задач, а также развитие логического мышления и умения анализировать информацию, позволит успешно справляться с задачами любой сложности.

Литература:

1. Теоретические основы начального курса математики: учеб. пособие для студ. учреждений сред. проф. образования / Л. П. Стойлова. — М.: Издательский центр «Академия», 2014. — 272 с

2. Методика работы с текстовыми задачами на уроках математики в условиях реализации ФГОС: учеб. пособие / сост. Т. В. Захарова, А. И. Пеленков, Е. Н. Яковлева, Т. В. Качурина, федеральный ун-т, 2017–102 с.

3. Стойлова Л. П. Математика / Л. П. Стойлова. — М.: Издательский центр «Академия», 2005–424 с.

4. Истомина Н. Б. Методика обучения математике в начальных классах /Н. Б. Истомина. — М.: Издательский центр «Академия», 2001–288 с.

5. Демидова Т. Е. Теория и практика решения текстовых задач / Т. Е.Демидова, А. П. Тонких. — М.: Издательский центр «Академия», 2002–288 с.

6. Истомина Н. Б. Мeтoдика oбучeния мaтeмaтикe в нaчaльных классах / Учеб. пoсoбиe для стyд. сpед. и высш. пед. учеб. заведений. — 4-е изд., стepеoтип. — М.: Издательский центр «Академия», 200l. — 288 с

7. Мамыкина, Л. А. Математическое моделирование как метод познания и обучения математике в профильной школе [Электронный ресурс] / Л. А. Мамыкина // Новосибирский государственный педагогический университет. 2008. — № 8. — С. 296–281. — Режим доступа: https://elibrary.ru/download/elibrary_18086876_92658059.pdf- Последнее обновление 12.05.2017.

8. Лященко Е. И. Лабораторные и практические работы по методике преподавания математики [Текст]: Учеб. пособие для студентов физ.-мат. 64 спец. пед. ин-тов / Е. И. Лященко, К. В. Зобкова, Т. Ф. Кириченко и др.; Под ред. Е. И. Лященко. — М.: Просвещение, 1988. — 223 с.

9. Орехов, Ф. А. Решение задач методом составления уравнений [Текст]: Пособие для учителей восьмилетней школы / Ф. А. Орехов. — М.: Просвещение, 1971. — 156 c.

10. Пойа, Д. Как решать задачу /Пер. с англ. В. Г. Звонаревой и Д. Н. Белла, под ред. Ю. М. Гайдука. — 2-е изд. — М.: Учпедгиз, 1961. — 207 c.

11. Столяр, А. А. Логические проблемы преподавания математики / А. А. Столяр.– Минск: «Высшая школа», 1965. — 254 с.

12. Фридман, Л.М., Теоретические основы методики обучения математике [Текст]: Учебное пособие / Л. М. Фридман. — Изд. 3-е. — М.: Книжный дом «ЛИБРОКОМ», 2009. — 248 с.

13. Практикум по методике обучения математике в начальной школе: Развивающее обучение / Н. Б. Истомина, Ю. С. Заяц. — Смоленск: Ассоциация XXI век, 2009–144 с.: ил.

14. Пирютко О. Н., Графический метод решения текстовых задач: учебное пособие / О. Н. Пирютко. — Минск: «Новое знание», 2010. — Режим доступа http://elib.bspu.by/handle/doc/23659