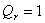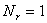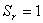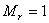Рассматриваются гармонические колебания двухслойных пластин с произвольными граничными условиями. Дается полный алгоритм решения задачи методом граничных интегральных уравнений. Получены фундаментальные динамические функции влияния перемещений и усилий.
Колебания тонких пластин могут быть значительно уменьшены с помощью демпфирующих покрытий [1,2]. С другой стороны, известно, что уравнения движения многослойных пластин с чередующимися мягкими и жесткими слоями также могут быть преобразованы к уравнениям для двухслойной пластинки [1]. Таким образом, теоретическое и экспериментальное изучение вибраций двухслойных пластин представляет собой важную задачу.
Система дифференциальных уравнений движения двухслойной пластинки в уточненной постановке с учетом сдвиговых деформаций в обоих слоях (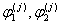
) приводится в [2]. Предположим, что для j=1 (поддерживающий слой) 
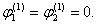В таком случае сдвиговые деформации учитываются только в демпфирующем покрытии(j=2).Система дифференциальных уравнений деформации пластинки принимает вид:
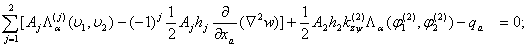
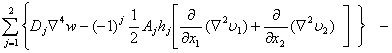(1)
(
)
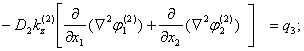
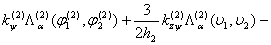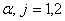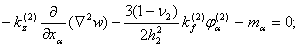
где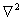 
- оператор Лапласса,
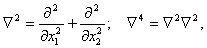
j –индекс слоя(j=1,2),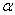 
- индекс координатных осей(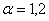
),
w,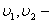
функции трансверсальных и осевых перемещений для точек на поверхности интерфейса;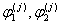-функции сдвиговых деформаций для слоя с индексом (j);
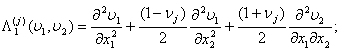
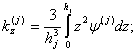
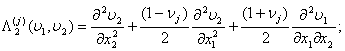
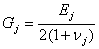(2)
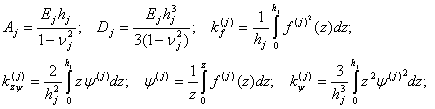
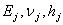— модуль упругости,коэффициент Пуассона и толщина слоя с индексом (j); 
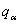- распределенные нагрузки в плоскости интерфейса(
);
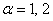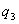-интенсивность трансверсальной нагрузки 
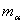-распределенная моментная нагрузка; 
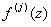- функция сдвигов.
Рассеяние энергии в демпфирующем покрытии может быть учтено введением комплексного модуля упругости: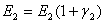 
(
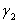- фактор потерь для демпфирующего покрытия).
Уравнения (1) могут быть преобразованы для описания колебаний различных частных моделей пластинки.
Если введенная в (2) функция f(z) является квадратичной, то имеем:
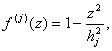и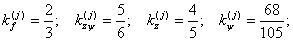 
(квадратичный закон распределения сдвигов [2]). Если функция f(z) =1(постоянняя):
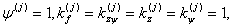(равномерное распределение сдвигов).
Предполагаем также, что: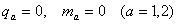 
Теперь введем в рассмотрение функции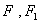 
[2]:
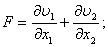
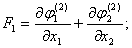(3)
Система (1) имеет пять уравнений.
Дифференцируем по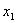 
первое уравнение (1) при 
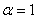и по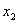 
то же самое уравнение при 
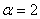а затем суммируем эти уравнения; далее используем ту же самую процедуру для четвертого и пятого уравнений системы (1). Таким образом, получим систему трех дифференциальных уравнений:
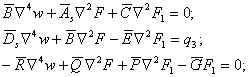(4)
где введены обозначения:
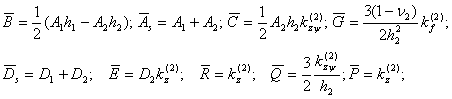(5)
Система дифференциальных уравнений (4) может быть заменена одним дифференциальным уравнением:
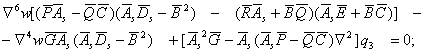(6)
Перейдем к полярной системе координат и представим функции, входящие в (6) функции в виде:
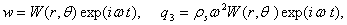(7)
Здесь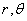
- полярные координаты,
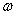— частота колебаний,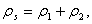 
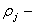распределенные массовые плотности.
С учетом (7), уравнение (6) принимает вид:
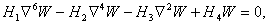(8)
где
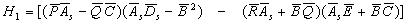(9)
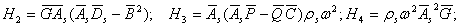
Следуя [3], будем искать решение (8) в виде:
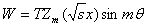(10)
где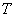 
-константа, 
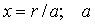-радиус пластинки. 
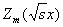-функция Бесселя индекса 
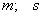- характеристический параметр.
Подставляя (10) в уравнение (8), мы получаем характеристическое уравнение относительно параметра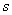 
.
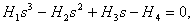(11)
Решения (11) при (учете демпфирования) являются комплексными числами, для которых справедливы следующие соотношения:
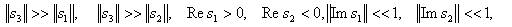
где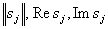
- соответственно модуль, действительная и комплексная части комплексного числа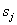 
С учетом этого, комплексный корень s3, соответствующий не изгибным формам деформации, может быть отброшен.
Решение (10) в общей форме можно записать:
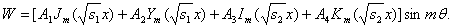(12)
Здесь
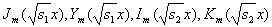-соответственно функции Бесселя первого рода и модифицированные функции Бесселя;
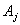-произвольные постоянные; 
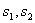-характеристические числа.
В дальнейшем удобно ввести в рассмотрение функции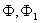
, связанные с функциями деформаций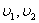
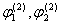соотношениями:
;
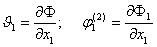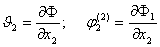; (13)
При подстановке (13) в (3) получим:
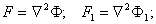(14)
Следствием системы дифференциальных уравнений задачи типа (4) являются зависимости вида:
(15)
где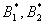 
множители, зависящие от параметра 
: 
.
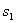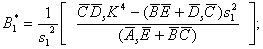
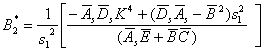Как и в случае однослойной пластинки [3], решение для функций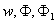 
при сосредоточенном трансверсальном воздействии
на бесконечную двухслойную пластинку (для m=0) разыскиваем в виде комбинации сингулярных при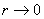 
цилиндрических функций.
С учетом (7.7) имеем:
; 
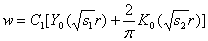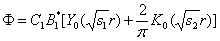
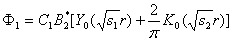(16)
где С1 –константа.
Справедливость соотношений (16) следует из представлений функций Y0,K0 при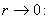 
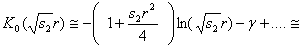
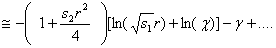(17)
; (
)
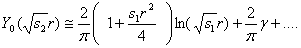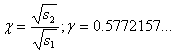Подстановка (17) в (16) приводит к взаимному уничтожению слагаемых, содержащих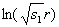 
.
Следствием (16) являются соотношения, определяющие перемещения в координатной системе, связанной с направлениями нормали (n) и касательной к контуру пластинки (t) (рис. 1).
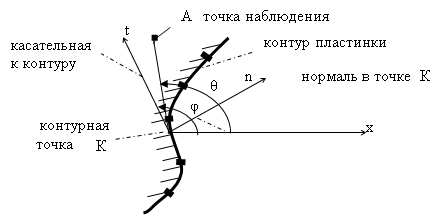
Рис. 1
Для упрощения преобразований введем функции:
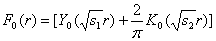, (18)
, 
.
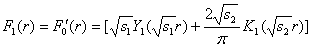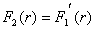В таком случае соотношения(16) принимают вид:
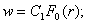
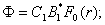
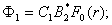(19)
Функции перемещений:
;
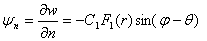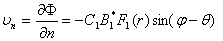; (20)
;
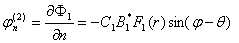Рассмотрим загружение пластинки сосредоточенной силой
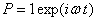. Поперечная сила 
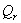для осесимметричного случая записывается в виде:
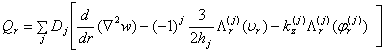, (21)
где в случае осесимметричного загружения имеем:
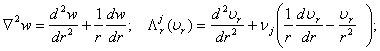(22)
В случае учета сдвигов только в подкрепляющем слое(j=2) выражение (21) преобразуется к виду:
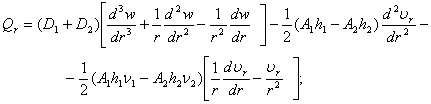(23)
Подставим (17),(19), (20) в (23) и выполним предельный переход:
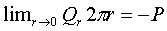
С учетом(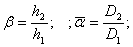
)получаем выражение для С1:
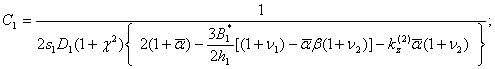(24)
Для данного загружения имеем:
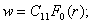
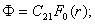
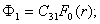(25)
где
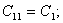
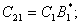
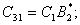(26)
Выражения (20) определяют фундаментальные функции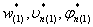
Остановимся на выводе функций влияния от действия кососимметричных динамических нагрузок, учитывая взаимосвязь функций перемещений и силовых факторов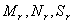 
.
Рассмотрим загружение нагрузкой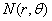
,расположенной в плоскости интерфейса:
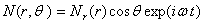; (27)
При 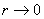получим предельный случай: действие сосредоточенной осевой единичной нагрузки:
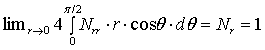; (28)
Здесь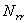 
с учетом 
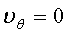имеет вид [2]:
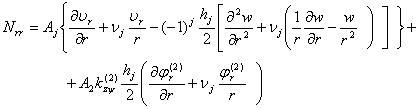(29)
Выполняя предельный переход в (29), получим:
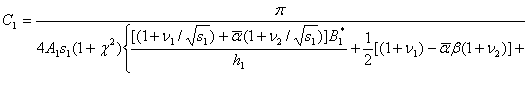
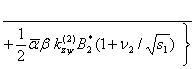(30)
Для этого варианта единичного загружения получим:
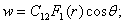
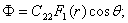
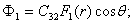(31)
где 
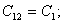
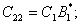
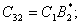(32)
Выражения (20) определяют фундаментальные функции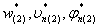
Точно также, рассматриваем загружение распределенными сдвиговыми моментами
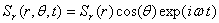; (33)
При 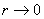имеем:
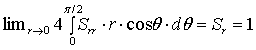(34)
Здесь
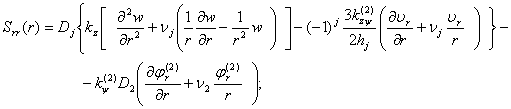(35)
В результате стандартных преобразований получим выражение для константы С1 для этого случая:
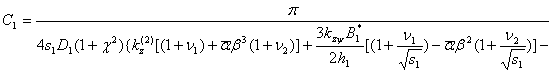
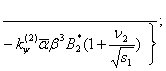(36)
Для этого варианта единичного загружения получим:
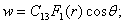
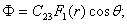
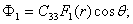(37)
где 
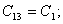
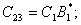
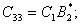(38)
Выражения (20) определяют фундаментальные функции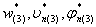
Рассмотрим загружение бесконечной пластинки моментной динамической нагрузкой, распределенной по окружности, и изменяющейся по закону:
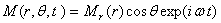(39)
Функции влияния для этого случая можно получить из соотношений для первого загружения, дифференцируя по нормали к контуру соответствующие случаю Р=1 функции. Отсюда ясно, что константы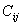 
для этого загружения остаются такими же по величине, как и в первом загружении,а выражения для функций влияния изменяются. Таким образом, для данного загружения можно записать:
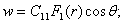
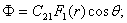
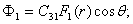(40)
Выражения (20) определяют фундаментальные функции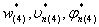
Определенные таким образом константы Cij образуют матрицу коэффициентов С и задают систему фундаментальных функций для перемещений.
Матрица коэффициентов С имеет вид:
|
|
|
|
|
|
С11 |
С12 |
С13 |
С14 |
|
С21 |
С22 |
С23 |
С24 |
|
С31 |
С32 |
С33 |
С34 |
(41)
Здесь учтено Ci4=Ci1 при (i=1,2,3)
Функции перемещений, соответствующие каждому загружению, удобно представить в тензорной форме:
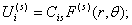(42)
где 
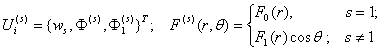(43)
В дальнейшем используем стандартную прямую формулировку задачи [3], основанную на принципе Бетти.
Обозначая: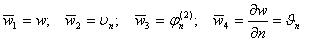 
, мы можем
записать систему четырех интегральных уравнений задачи в виде одного тензорного уравнения, вида:
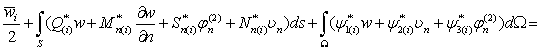
(44)
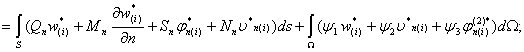
Здесь звездочкой помечены основные динамические функции влияния для перемещений и усилий, расположенных на контуре двухслойной пластинки;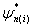 
-функции влияния гармонической внешней нагрузки, расположенной на пластинке.
Динамические функции влияния усилий на контуре пластинки определяются с учетом направления нормали к контуру.
Например, для функции влияния момента в направлении нормали к контуру можем записать:
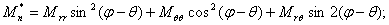(45)
где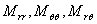 
определяются по известным формулам [2], выраженным в полярной системе координат, с помощью соотношений (20) для соответствующих загружений.
Окончательно для загружения j=1 имеем:
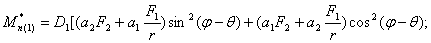
где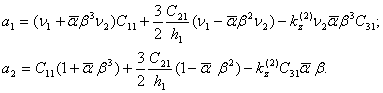 
(46)
Для загружений j=2,3,4:
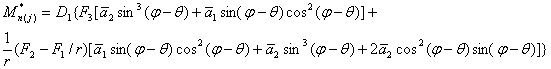
где
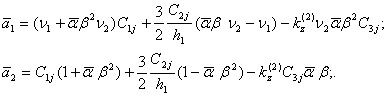(47)
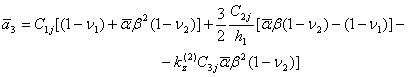
Вид остальных операторов (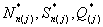
) имеет аналогичную структуру.
Дальнейший путь решения носит стандартный характер [5]. Контур пластинки аппроксимируется N граничными элементами. Для вычисления граничных и контурных интегралов используются квадратурные формулы. Получаем систему алгебраических уравнений относительно узловых усилий и перемещений на контуре пластинки.
Рис. 2 иллюстрирует применение рассматриваемой методики для расчета квадратной, шарнирно опертой по контуру двухслойной пластинки на действие сосредоточенной гармонической силы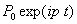 
,приложенной в центре пластинки(
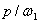=0.9–отношение частоты внешнего воздействия к первой частоте собственных колебаний). Пластинка имеет следующие параметры: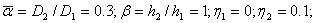 
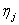-факторы потерь по гипотезе комплексных модулей упругости
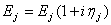координатной линии X1, проходящей через центр пластинки при различном числе узлов разбиения на стороне пластинки (а=1).
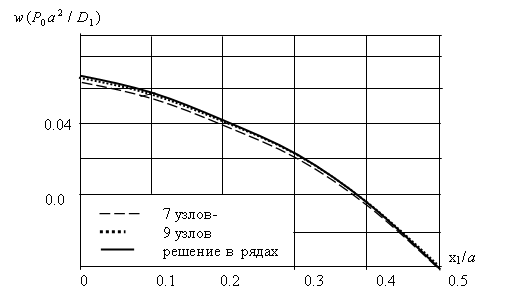
Рис. 2
Графики свидетельствуют о хорошем приближении к результатам, полученным в тригонометрических рядах. Динамические функции влияния для квадратной пластинки могут быть использованы в решении задач гашения колебаний пластин с помощью комбинированных средств виброзащиты, включающих демпфирующие покрытия и гасители колебаний.
Литература:
1. Nashif A., Johes D., Henderson J. Vibration damping. 1985,New York:John Wiley & Sons.
2. Болотин В. В., Новичков Ю. Н. Механика многослойных конструкций М.: Машиностроение, -1980.-375 с.
3. Коренев Б. Г. Некоторые задачи теории упругости и теплопроводности, решаемые в бесселевых функциях. М.: Физматгиз, 1960, -490 с.
4. Бенерджи, Прадип К, Баттерфилд Р. Методы граничных элементов в прикладных науках. М.: Мир, 1984, — 494.
