В работе исследуется напряженно-деформированное состояние диссипативно-однородных систем под действием активных сил. Получены численныерезультаты относительно подвижной координаты.

In work the intense-deformed condition of dissipative-homogeneous systems under the influence of active forces is investigated. Numerical results concerning mobile co-ordinate are received.

Рассматривается тонкая, бесконечно длинная цилиндрическая оболочка, взаимодействующая со своей внешней поверхностью относительно легким слоем (рис.1). Вдоль мягкого слоя с постоянной скоростью С, меньшей скорости распространения волн сдвига в слое, движется осесимметричная нормальная нагрузка. Уравнение движения мягкого слоя записывается в виде

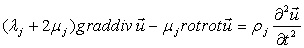,                                                          (1)

где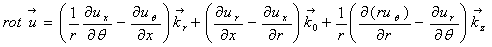

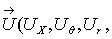) — вектор перемещения точек мягкого слоя. (j=0.1)

Уравнения движения оболочек в перемещениях в символической матричной форме запишем в виде

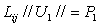.                                                                                                             (2)

Здесь U₁ –вектор перемещения точек срединной поверхности оболочек, причем для оболочек Кирхгофа — Лява он имеет размерность, равную трем.

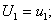
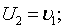
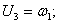   L_ij — матрицы дифференциальных операторов теории оболочек, включающая в задачах динамики и дифференцирование по времени (члены с демпфированием и инерционные члены в развернутом виде) приведена в работе [1]. Контакт между оболочкой и слоем принимается скользящими, а связь двухсторонней. Исследуется реакция оболочки на действие подвижной нагрузки и оценивается влияния жесткости и толщины амортизирующего слоя на величину резонансной скорости

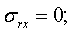
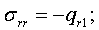
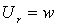
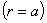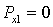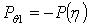
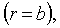; ;            (3,а)

где a и b — наружный и внутренний радиусы.

Если граница области, в которой изучается волновое поле, уходит в бесконечность, тогда требуются дополнительные условия в бесконечности. В первые эти условия получены Зоммерфельдом и подробно обсуждены в работе [1]. Здесь r радиус в цилиндрической системе координат. На границе мягкого слоя с упругой средой, выполняется условие жесткого контакта, т. е. выполняется условие равенства соответствующих перемещений и напряжений

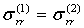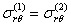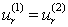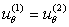; ; ; .                                                       (3,б)

При решении задачи (1) и (2) применяется преобразование Галилея

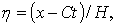                                                                                                          (4)

где Н - некоторая характерная в рассматриваемой задаче величина, имеющая размерность длин (для пластин это толщина, для оболочек –радиус внешнего или внутреннего слоя). С помощью преобразования (3) в рассматриваемых стационарных задачах исключаются независимое переменное время — t и вводится в уравнения параметр С (скорость движения нагрузки). В подвижной системе координат, определяемой согласно (4), задача сводится к совместному интегрированию уравнений движений оболочки (1), (2) и граничных условий на поверхности слоя (3,б). Применим в подвижной системе координат к уравнениям движения и граничным условиям комплексное преобразование Фурье [2].

Записывая общие решения преобразованных уравнений движения слоя в виде (1), (2) и (3), находим следующую систему алгебраических уравнений для определения безразмерных трансформант перемещений срединой поверхности

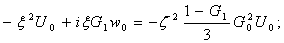                                                                (5)

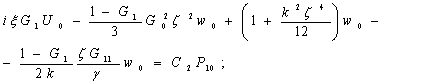
Где ;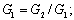

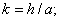
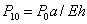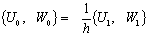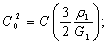;  a₁- толщина и радиус срединной поверхности оболочки соответственно; 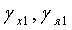-коэффициент демпфирования в осевом и радиальном направлениях.

Находим следующее выражение для трансформанты нагрузки, которая передается на оболочку со стороны мягкого слоя

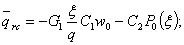
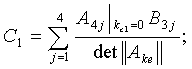
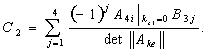
Элементы определителя 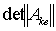 вычисляются по формулам

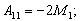
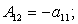
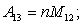
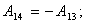
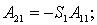
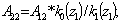
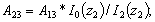
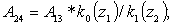
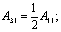
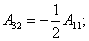
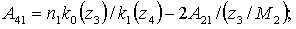
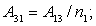
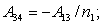
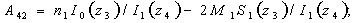
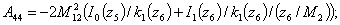
где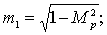    

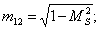
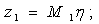
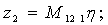
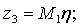
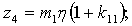
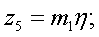
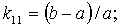
Здесь d = ρ/ρ_в представляет собой отношение плотности окружающей среды на плотность мягкого слоя; 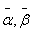 — являются функциями x и h;  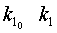-модифицированные функции Неймана;  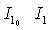-модифицированные функции Бесселя; Общее решение уравнений движений окружающей среды имеет вид  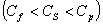[3]

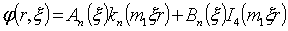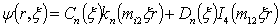, (6)

Выражение для трансформанты нормального перемещения имеет вид

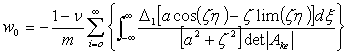                                                (7)

Определим 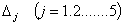 получаемый из  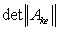заменой j=20 столбцов с элементами {0;0;1;0;0}. После этого функции из (7) могут быть вычислены по формулам

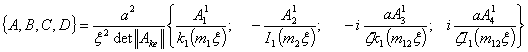
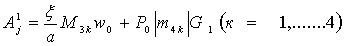
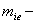миноры элемента А_je. Для конкретного значения скорости движения нагрузки С знаменатели под интегральных выражений в формулах (7) являются трансцендентными функциями относительно 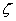с действительными коэффициентами, зависящими от С, а также от механических параметров оболочки и слоя.

Анализ интегралов обращения необходимо начинать с рассмотрения случаев 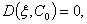 что эквивалентно построению дисперсионной зависимости в соответствующей задаче о распространении свободных волн и нахождению из дисперсионных кривых корней знаменателя для выбранной скорости движения нагрузки С. при С< С_S. Для заданной скорости С имеется один или два различных корня знаменателя (7), для некоторых значение С знаменатель имеет двойной корень. Этому случаю отвечает минимум coответствующей дисперсионной кривой на рис.1. Такая скорость движения называется резонансной и обозначается С^х. Появляется резонансный эффект, при котором прогибы и контактное давления стремятся к бесконечности. Для данного значения С знаменатель не имеет корней на действительной оси.

Разделив интеграл (7) на два слагаемых

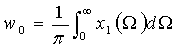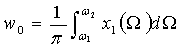 или ,                                  (8)

величину интеграла (8) найдем численно с помощью метода Ромберга [2].

При вычислении интеграла по методу Ромберга приходится многократно вычислять подынтегральную функцию. Показано, что при длине шага интегрирования 0,01 погрешность процедуры не превышает 0,3–0,5 %.

На рис. 1 изобрежено распределение контактных напряжений по верхней границе заполнителя при движении по внутренний поверхности трехслойной оболочки кольцевой нормальной нагрузки. Расчеты проведены для К_s=30; С₀₁=0.055. Кривые 1 соответствуют решению для рассматриваемой конструкции 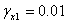, , 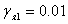при жестком контакте между несущими слоями и заполнителем; 2-соответствуют решению для рассматриваемой конструкции 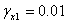, , 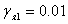при скользящем контакте между несущими слоями и заполнителем; 3 -отсутствия мягкого слоя; 4-оболочке , .

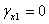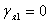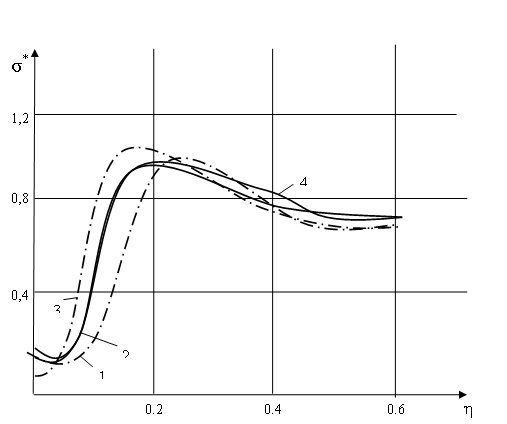
Рис. 1. Изменение контактных напряжений на границе заполнителя и нагруженной обшивки

Выявлено, что контактные напряжения с удалением от места приложения нагрузки меняют знак, что является следствием предложения о двусторонней связи заполнителя с несущим слоем и свидетельствует о возможности отрыва нагруженной радиальной нагрузкой оболочки от заполнителя.

Литература:

1.                  Сафаров И. И. Колебания и волны в диссипативно неоднородных средах и конструкциях. — Ташкент: ФАН, 1992. — 250с.

2.                  Бозоров М. Б., Сафаров И. И., Шокин Ю. И. Численное моделирование колебаний диссипативно однородных и неоднородных механических систем. — Новосибирск: СО РАН, 1966, — 188с.

3.                  Горшков А. Г., Пожуев В. И. Стационарные задачи динамики многослойных конструкций. — М.: — 223с.