В работе рассматривается распространение гармонических волн в цилиндрической панели с переменной толщиной. Для вывода уравнений оболочки использован принцип возможных перемещений. Решения краевой задачи получены методом ортогональной прогонки Годунова. Были исследованы дисперсионные кривые в зависимости от различных геометрических параметров системы.
Рассматривается деформированная бесконечная цилиндрическая оболочка толщиной h, плотности ρ, с модулем Юнга Е, коэффициентом Пуассона 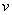 и вязкоупругих свойств материала. В криволинейной ортогональной системе координат (α1; α2; z) при z = 0 оболочка занимает область
и вязкоупругих свойств материала. В криволинейной ортогональной системе координат (α1; α2; z) при z = 0 оболочка занимает область
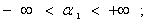
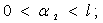
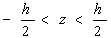 . Кривизны срединной поверхности z=0 равны
. Кривизны срединной поверхности z=0 равны 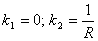 соответственно координатам α1 и α2. В рамках гипотез Кирхгофа — Лява закон изменения компонент вектора перемещений u1(z), u2(z), w(z) оболочки определяются следующими соотношениями [1,2]
соответственно координатам α1 и α2. В рамках гипотез Кирхгофа — Лява закон изменения компонент вектора перемещений u1(z), u2(z), w(z) оболочки определяются следующими соотношениями [1,2]
u1(z) = u — θ1z; u2(z)= v — θ2 z; u3(z) = w, (1)
где u, v, w — компоненты вектора перемещений срединной поверхности; θ1, θ2 — углы поворота нормали относительно осей α1 и α2. Для вывода уравнений оболочки, использовался принцип возможных перемещений. В свою очередь, усилия и моменты связаны с компонентами деформации определяющимися соотношениями, вытекающими из обобщенного закона Гука:
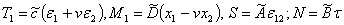
где
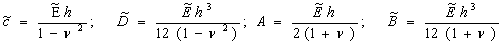
E — операторный модуль упругости, которые имеют вид:
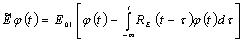
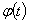 -произвольная функция времени;
-произвольная функция времени; 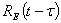 -ядро релаксации;
-ядро релаксации; 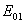 -мгновенной модуль упругости;
-мгновенной модуль упругости; 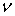 -коэффициент Пуассона, которая предлагается, что постоянная величина. Если пренебречь инерцией поворота нормали, то виртуальную работу силы инерции оболочки можно представить в виде:
-коэффициент Пуассона, которая предлагается, что постоянная величина. Если пренебречь инерцией поворота нормали, то виртуальную работу силы инерции оболочки можно представить в виде:
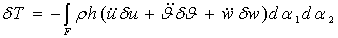 (2)
(2)
После подстановки выражения (2) в уравнение принцип возможных перемещений и стандарта процедуры интегрирования по частям, получаем уравнения движения в виде:
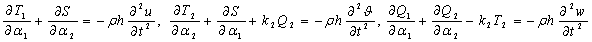
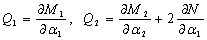 (3)
(3)
Альтернативные краевые условия свободного края, или жесткой заделки, при α2 = 0, имеют вид:
свободный край
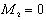 ;
;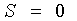 ;
;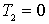 ;
;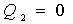 (4)
(4)
жесткая заделка
u=0, v=0, w=0, q2=0 (5)
Используя соотношения (3), (4) и (5) полную систему уравнений движения можно представить в виде восьми дифференциальных уравнений, размешенных относительно первых производных по α2. В случае бегущих вдоль α1 гармонических волн решения краевой задачи для полуених системы (5) с краевыми условиями типа (4), (5) допускают разделение переменных
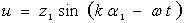 ;
; 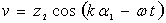 ;
; 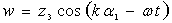 ;
;
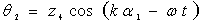 ;
;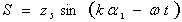 ;
; 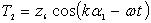 ; (6)
; (6)
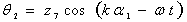 ;
; 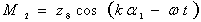 ;
;
где 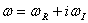 - комплексная собственная частота; к- волновое число, действительная величина;
- комплексная собственная частота; к- волновое число, действительная величина; 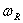 -действительная часть комплексной частоты;
-действительная часть комплексной частоты; 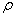 -плотность;
-плотность; 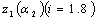 - функции формы колебаний.
- функции формы колебаний.
Далее предполагается, что оба края оболочки 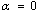 и α1= l — свободны. После подстановки соотношений (6) в уравнения (3) учитывая и краевые условия (4) имеем спектральную краевую задачу по параметру
и α1= l — свободны. После подстановки соотношений (6) в уравнения (3) учитывая и краевые условия (4) имеем спектральную краевую задачу по параметру 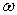 для системы восьми обыкновенных дифференциальных уравнений относительно комплексной функции формы:
для системы восьми обыкновенных дифференциальных уравнений относительно комплексной функции формы:
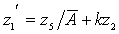
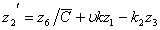
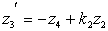
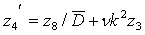
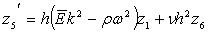 (7)
(7)
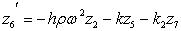
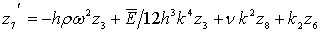 ;
; 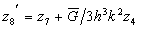 ;
; 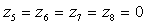 ;
; 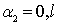
Е выражаются через операторные модули упругости: .
.
Здесь 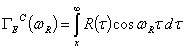 ,
, 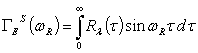 , соответственно, косинус и синус образы Фурье ядра релаксации материала. В качестве примеры вязкоупругого материала примем трех параметрические ядра релаксации
, соответственно, косинус и синус образы Фурье ядра релаксации материала. В качестве примеры вязкоупругого материала примем трех параметрические ядра релаксации 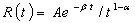 , обладающее слабой сингулярностью [2]. При анализе дисперсии гармонических волн параметр к считается заданным.
, обладающее слабой сингулярностью [2]. При анализе дисперсии гармонических волн параметр к считается заданным.
На основе решения краевой задачи (7) методом ортогональной прогонки Годунова был выполнен численный анализ дисперсии этих волн.
- с ростом кривизны цилиндрической панели постоянной толщины увеличивается реальные части комплексной 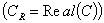 скорости распространения первой изгибной моды и уменьшается скорость распространения второй крутильной моды так, что, начиная с некоторого значения параметра кривизны, моды дважды пересекаются между собой. С увеличением кривизны увеличивается также число узловых точек формы колебаний прогиба;
скорости распространения первой изгибной моды и уменьшается скорость распространения второй крутильной моды так, что, начиная с некоторого значения параметра кривизны, моды дважды пересекаются между собой. С увеличением кривизны увеличивается также число узловых точек формы колебаний прогиба;
- в случае клиновидной цилиндрической панели для каждой моды существуют предельные скорости распространения при увеличении волнового числа, совпадающие по величине с соответствующими скоростями нормальных волн в клиновидной пластине нулевой кривизны. В коротковолновом диапазоне локализация движения существует и увеличивается с ростом кривизны панели. Число узловых точек формы колебаний прогиба зависит не только от кривизны, но и от волнового числа.
Литература:
1. Новожилов В. В. Теория тонких оболочек– Л.: Судпромгиз,1962.-431с.
2. Колтунов М. А. Ползучесть и релаксация -М.: Высшая шкала,1976.-277с.
3. Бозоров М. Б., Сафаров И. И., Шокин Ю. И. Численное моделирование колебаний диссипативно однородных и неоднородных механических систем. СО РАН, Новосибирск, 1996.- 188с.

