В статье рассматривается применение математического моделирования для построения геометрических объектов в среде MathCAD. На примере модели сферы, условно называемой «апельсинкой», демонстрируются возможности программного комплекса для визуализации математических формул и геометрических тел. Описываются теоретические основы построения модели, её практическое значение, а также проводится анализ существующих решений для математического моделирования.

Ключевые слова: математическое моделирование, MathCAD, сфера, визуализация, геометрические объекты.

Введение

Математическое моделирование является одним из фундаментальных методов научного познания, обеспечивающих воспроизведение, исследование и прогнозирование свойств сложных объектов и процессов. Оно позволяет формализовать реальные явления, выявлять их внутренние закономерности и на основе этого находить практические решения для задач различного уровня сложности. В условиях стремительного развития науки и техники моделирование приобретает особую значимость, поскольку традиционные методы анализа зачастую оказываются недостаточными для работы с многопараметрическими и междисциплинарными системами.

Актуальность данной работы определяется несколькими факторами. Во-первых, возрастающей ролью информационных технологий в образовании и науке, где особое внимание уделяется наглядности и интерактивности учебных материалов. Во-вторых, необходимостью подготовки специалистов, способных не только оперировать абстрактными математическими конструкциями, но и использовать современные программные комплексы для их визуализации и анализа. В-третьих, задачей повышения мотивации обучающихся, для чего требуется интеграция классических методов преподавания с инновационными средствами представления информации.

Как отмечал Н. Н. Моисеев, «Построение математических моделей является основой всего системного анализа. Это — центральный этап исследования или проектирования любой системы. От качества модели зависит судьба всего последующего анализа… Модель должна правильно отражать явления, однако одного этого ещё мало. Она должна быть удобной для использования. Поэтому степень детализации модели, форма её представления определяются целями исследования и непосредственно зависят от исследователя» [1] (Моисеев, 1981, с. 138). Данное утверждение сохраняет актуальность и в настоящее время, когда математическое моделирование становится не только инструментом науки, но и важнейшей составляющей образовательного процесса.

Объектом настоящего исследования является процесс построения и визуализации геометрических объектов средствами программного комплекса MathCAD. В качестве демонстрационного примера рассматривается модель сферы, условно называемая « апельсинка ».

Цель работы заключается в анализе возможностей MathCAD для создания наглядных математических моделей, а также в определении их методической ценности в образовательной практике.

Задачи исследования включают:

– описание теоретических основ построения модели сферы;

– демонстрацию возможностей MathCAD для визуализации формул и трёхмерных объектов;

– обоснование практической значимости использования таких моделей в учебном процессе;

– проведение анализа существующих подходов к математическому моделированию и выявление преимуществ применения рассматриваемого программного комплекса.

Практическая значимость исследования состоит в том, что полученные результаты могут быть использованы в учебной деятельности для повышения наглядности изложения материала, формирования у студентов системного мышления и навыков работы с современными средствами математического моделирования.

Обзор существующих решений

Сегодня существует множество программных комплексов, которые используются для математического моделирования и визуализации геометрических объектов. Наиболее известные из них — MATLAB, Maple, Mathematica, а также инженерные CAD-системы вроде AutoCAD и SolidWorks. Каждая из этих сред имеет свои преимущества, но в то же время накладывает определённые ограничения на работу пользователя.

MATLAB широко применяется в инженерных расчётах и обработке численных данных. Он позволяет строить графики функций и поверхностей, но требует хорошего знания языка программирования, что делает его менее удобным для начального обучения.

Maple и Mathematica ориентированы на символьные вычисления и прекрасно подходят для решения сложных аналитических задач. Однако для студентов младших курсов и школьников они могут оказаться излишне сложными и перегруженными функциями.

CAD-системы, такие как AutoCAD или SolidWorks, обеспечивают высочайшую точность построений и активно используются инженерами-проектировщиками. Тем не менее, эти системы не предназначены для работы с математическими формулами в их привычной учебной записи и требуют длительного освоения.

На этом фоне особенно выделяется MathCAD — программа, которая занимает промежуточное, но уникальное положение между математическими пакетами и инженерными CAD-системами. Главным её достоинством является возможность работать с формулами в естественном виде: пользователь вводит выражения так же, как в учебнике, а не в виде кода. Как подчёркивает А. А. Алямовский, «главное достоинство Mathcad заключается в том, что математические выражения вводятся в привычной для пользователя форме, аналогичной записи в учебнике. Это делает работу в среде доступной даже для начинающих» [2] (Алямовский и др., 2012, с. 5).

MathCAD сочетает символьные и численные вычисления, что позволяет не только преобразовывать уравнения, но и выполнять конкретные расчёты. По мнению В. С. Пугачёва, «Mathcad сочетает численные и символьные методы вычислений, при этом обеспечивая визуализацию результатов в виде графиков и таблиц. Такая интеграция делает программу особенно эффективной в образовательном процессе» [3] (Пугачёв, 2011, с. 12). Важным преимуществом является то, что все изменения в формулах сразу отражаются в связанных графиках и таблицах, благодаря чему достигается высокая интерактивность работы.

Особенно ценным для учебного процесса является встроенная возможность визуализации: MathCAD легко строит двумерные и трёхмерные графики, включая поверхности и параметрические кривые. При этом интерфейс остаётся интуитивно понятным даже для начинающих пользователей. Как отмечает Е. И. Кочетков, «использование Mathcad в учебной практике позволяет формировать у студентов навыки математического моделирования в наглядной и интуитивно понятной форме. Это существенно снижает барьер в освоении сложных дисциплин» [4] (Кочетков, 2006, с. 18).

По сравнению с MATLAB, где построение графиков требует написания кода, MathCAD обеспечивает гораздо более простую и наглядную работу. В отличие от Maple и Mathematica, он менее перегружен функциями, что делает его оптимальным для образовательных целей.

Следует отметить, что MathCAD всё же имеет ограничения: он уступает Maple и Mathematica в области сложных символьных вычислений и не может заменить CAD-системы для промышленного проектирования. Однако именно в области учебных задач и базового математического моделирования он остаётся наиболее удобным и эффективным инструментом.

Таким образом, MathCAD можно рассматривать как «золотую середину» между громоздкими профессиональными системами и узкоспециализированными пакетами. Его простота, наглядность и гибкость делают программу идеальной для построения моделей, подобных «апельсинке», где требуется одновременно математическая строгость и визуальная выразительность.

Метод и описание построения модели

Для построения модели «апельсинки» в среде MathCAD используется параметрическое уравнение сферы, которое выражается через углы  _i и  _j . Введённые пользователем формулы имеют привычный вид, что является одним из ключевых преимуществ MathCAD:

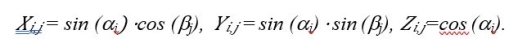
Задавая радиус R и диапазоны изменения параметров i и j , программа автоматически строит трёхмерную поверхность. При этом изменяя шаг дискретизации, можно регулировать детализацию изображения: меньший шаг обеспечивает более гладкую поверхность, а больший — формирует упрощённую геометрию.

Таким образом, формулы непосредственно «управляют» визуализацией: любое изменение выражений сразу отражается в построенной модели. На основе этих зависимостей получается объект, визуально напоминающий целый фрукт — условная «апельсинка» (рис. 1).

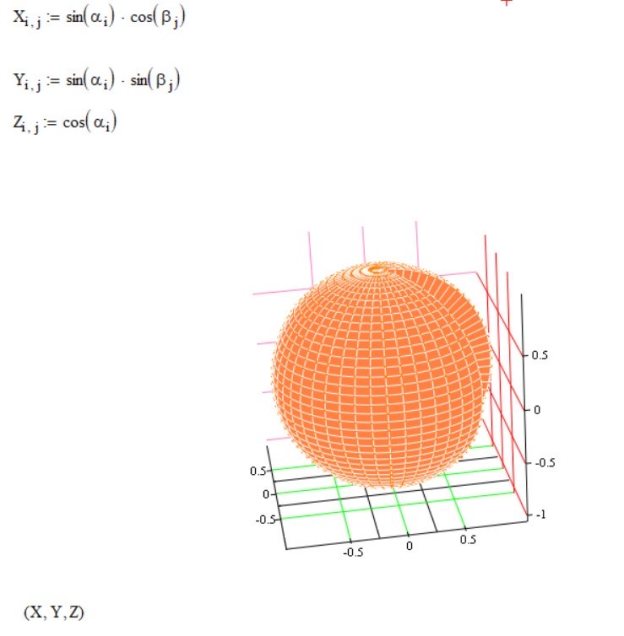
Рис. 1. «Апельсинка»

Дополнительно можно задать условие исключения части поверхности, что приводит к построению модели «апельсинки с долькой» (рис. 2). Такой приём демонстрирует не только возможности среды MathCAD по работе с параметрическими уравнениями, но и показывает, что абстрактные математические формулы могут иметь наглядное и практическое представление.

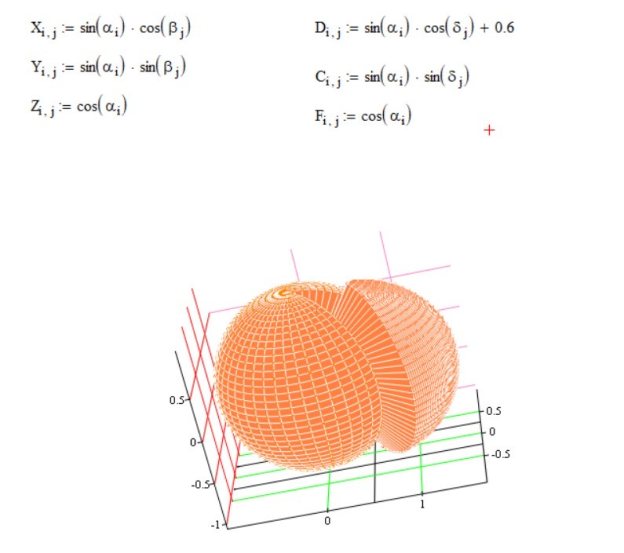
Рис. 2. «Апельсинка с долькой»

Результаты и исследование

Полученная модель «апельсинки» наглядно показала, что среда MathCAD эффективно справляется с задачей визуализации математических объектов и уравнений. Построение сферы в параметрической форме подтвердило, что даже достаточно сложные математические зависимости могут быть представлены в доступном и понятном виде. Такой подход особенно важен в учебной практике, так как позволяет студентам быстрее понять геометрический смысл уравнения и соотнести его с реальными объектами из окружающего мира.

Эксперимент подтвердил интерактивные возможности MathCAD: любое изменение исходных параметров модели, например, радиуса, моментально отражается на построенной поверхности. Это создаёт условия для проведения исследовательских экспериментов в реальном времени, когда студенты могут варьировать значения и сразу наблюдать результат. Дополнение модели «долькой» сделало её ещё более наглядной, усилив ассоциативное восприятие и показав, что даже абстрактные формулы могут быть интерпретированы в образной форме.

Таким образом, проведённое исследование подтвердило, что MathCAD подходит не только для решения абстрактных задач, но и для визуализации объектов, близких к повседневной жизни. Это значительно повышает интерес к предмету и облегчает понимание сложных математических понятий. В современных условиях цифровизации образования такой подход приобретает особую актуальность: он позволяет сделать обучение более интерактивным, доступным и мотивирующим.

Модель «апельсинки» продемонстрировала практическую ценность MathCAD как инструмента обучения и исследовательского анализа, показав, что программа может использоваться не только в профессиональной инженерной среде, но и в образовательных целях для формирования прочных знаний и развития пространственного мышления.

Выводы

В работе показано, что MathCAD — это удобный и эффективный инструмент для моделирования простых геометрических объектов. Построение модели «апельсинки» показало, что программа сочетает наглядность, простоту работы и достаточно широкие возможности для построения параметрических уравнений. На этом примере подтверждена практическая ценность MathCAD как средства обучения и проведения исследовательских задач, где важно не только получить точный результат, но и представить его в наглядной форме.

Модель сферы может использоваться в образовательной практике как иллюстрация при изучении математики, физики, информатики и инженерных дисциплин. Благодаря наглядности, студенты легче понимают абстрактные формулы и быстрее устанавливают связь между математической записью и её геометрическим образом. Такой подход помогает развивать пространственное мышление и повышает интерес к предмету.

В дальнейшем на основе тех же принципов можно создавать более сложные модели. Это могут быть как другие геометрические фигуры (например, многогранники или поверхности вращения), так и объекты из других областей знаний.

Таким образом, представленная работа является первым шагом к более широким исследованиям. В перспективе важно рассматривать моделирование не только простых сфер, но и более сложных структур, где требуется сочетание математической строгости и выразительной графики. Это позволит полнее раскрыть возможности MathCAD как современного инструмента математического моделирования и визуализации.

Литература:

1. Моисеев Н. Н. Математические задачи системного анализа. — М.: Наука, 1981. — 488 с.
2. Алямовский А. А., Собачкин А. А., Харитонов В. В. Mathcad 15. Самоучитель. — СПб.: БХВ-Петербург, 2012. — 688 с.
3. Пугачёв В. С. Mathcad: основы и примеры использования. — М.: ДМК Пресс, 2011. — 320 с.
4. Кочетков Е. И. Вычислительные технологии. Mathcad. — М.: Физматлит, 2006. — 272 с.