В статье автор описывает основные численные методы. Определено, что метод коллокаций на базе матриц дифференцирования и интегрирования позволяет получить точные решения при существенно меньших вычислительных затратах, что делает его актуальным инструментом в задачах, требующих высокой точности.Автор приходит к выводу, что выбор метода — определяется задачей и самое важное — насколько точно он передаёт физику задачи.

Ключевые слова: численный анализ, численные методы, метод коллокаций.

Одномерные модели теплопроводности играют ключевую роль в численном анализе процессов теплообмена как в теоретических исследованиях, так и в прикладных задачах инженерной и научной практики. Температурные поля в стержнях, нитях, каналах, микросенсорах и волоконных структурах описываются именно такими уравнениями. Несмотря на кажущуюся простоту, даже одномерная задача остаётся непростой с вычислительной точки зрения, особенно если требуется высокая точность при ограниченных ресурсах [2].

Численных методов много, и каждый из них предлагает свой взгляд на одну и ту же проблему — решение уравнения [3]. Чтобы понять, зачем использовать метод коллокаций, стоит сопоставить его с другими подходами, принятыми в научной и инженерной практике.

Метод конечных разностей можно назвать классическим. Локальные аппроксимации, жёсткая связь с геометрией, простота реализации — вот его сильные стороны. Но метод не любит кривых границ и теряет точность, если решение быстро меняется. При равномерной сетке появляются трудности с описанием процессов у краёв области, а порядок сходимости ограничен, чаще всего вторым.

Метод конечных элементов по-настоящему гибкий. Вместо равномерной сетки используется адаптивное разбиение, а аппроксимация строится кусочно. Он идеально подходит для сложных геометрий, позволяет встроить условия сопряжения, легко масштабируется на многомерные задачи. Но его реализация требует большего объёма работы, матрицы становятся разреженными, но громоздкими, а приращение точности не всегда оправдывает вычислительные затраты.

Метод Рунге — Кутты и его модификации. Их используют, когда задача зависит от времени, а по пространству всё уже дискретизировано. Это методы шагового интегрирования, они строят решение от одного момента времени к другому, используя информацию о производной. Преимущество — в высокой точности и адаптивности по шагу, недостаток — в слабой связи с пространственным аппроксиматором. Если сетка выбрана плохо, никакая Рунге–Кутта не спасёт решение от искажений.

Когда требуется добиться высокой точности без чрезмерного усложнения сетки, стандартные методы не всегда отвечают необходимым требованиям. В таких случаях возможно применение метода коллокаций — подход, в котором аппроксимация охватывает всю область, а не локально прицепляется к соседним узлам. Он использует полиномы как строительный материал, а в качестве фундамента берёт значения уравнения в особых коллокационных точках.

В основе метода лежит идея: вместо того чтобы решать уравнение в непрерывной форме, подставим приближение решения — в виде линейной комбинации базисных функций — и потребуем, чтобы оно точно удовлетворяло уравнению в заранее выбранных точках внутри области. Эти точки — не просто числа на оси, а якоря, через которые проходят все вычисления. Именно в них приближённая функция должна «соблюдать» дифференциальное уравнение.

Допустим, ищем решение (x)виде суммы:

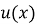
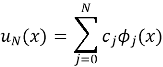
где — базисные функции (часто берут полиномы Лагранжа, Чебышёва или Лежандра), а — коэффициенты, которые нужно определить. Далее подставляем в исходное уравнение и требуем, чтобы оно выполнялось точно в точке .

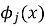
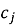
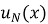
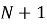
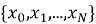
Такое требование превращает задачу в систему алгебраических уравнений относительно коэффициентов . Результат — аппроксимация, которая не «примерно» решает уравнение, а «жёстко» подчиняется ему в выбранных местах. Это создаёт баланс между глобальной точностью и локальным контролем.

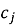
Особенность метода — в его чувствительности к выбору узлов. Расставлять точки равномерно в некоторой степени опасно: полиномы высокого порядка на равномерной сетке легко порождают осцилляции (эффект Рунге). Поэтому чаще используют специальные распределения, такие как узлы Чебышева, которые концентрируются ближе к краям интервала и стабилизируют аппроксимацию.

Метод коллокаций демонстрирует особенно высокую эффективность при решении задач с гладкими решениями. Он быстро сходится и обеспечивает точность, недостижимую для методов, основанных на локальной аппроксимации. Более того, его легко адаптировать к задачам со сложными граничными условиями, неоднородностями и нелинейностями [1, с. 226].

Метод коллокаций использует глобальный подход: приближает функцию на всей области сразу, не дробя её на отрезки. Такая стратегия даёт точность, недостижимую для локальных методов, особенно при гладком решении. Коллокации не нуждаются в равномерных сетках, так как они легко встраивают узлы Чебышева или Лежандра, что улучшает поведение аппроксимации вблизи границ. Более того, вся процедура базируется на линейной алгебре, без сложных трансформаций, разметок или разностных схем.

Однако стоит признать: метод коллокаций не универсален. Он теряет эффективность там, где решение обладает разрывами или локальными особенностями. Кроме того, глобальные матрицы чувствительны к росту размерности. Так, в задачах высокой размерности метод становится затратным. Тем не менее, при правильной постановке и выборе базиса, метод коллокаций превращается в точный и элегантный инструмент численного анализа.

Итак, выбор метода — это не вопрос моды. Это компромисс между точностью, устойчивостью, адаптивностью и вычислительной ценой. Методы конечных разностей и элементов хороши для широких инженерных применений, Рунге–Кутта выбираются для временной эволюции, а коллокации используются для задач с гладкой структурой, где нужна максимальная точность при минимальном числе узлов. Главное — не метод сам по себе, а то, как точно он передаёт физику задачи.

Литература:

1. Беляев В. А. Об эффективной реализации и возможностях метода коллокации и наименьших квадратов решения эллиптических уравнений второго порядка // Вычислительные методы и программирование. 2021. 22, 211–229. doi 10.26089/NumMet.v22r313.

2. Берлянд А. И., Гилев П. М. Численные методы в задачах теплопроводности. — Новосибирск: Наука, 1982. 296 с.

3. Гаврилов С. П. Численные методы в задачах математической физики. — М.: ФИЗМАТЛИТ, 2014. 368 с.