Рассмотрим краевую задачу (1)-(14) в [1].

Пусть

=

и где, i=1,2.

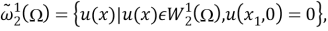
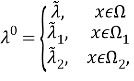
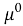
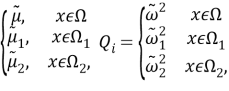
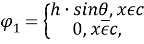
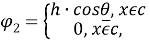
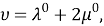
Систему уравнений (5) в [1] запишем в виде

— (1)

—

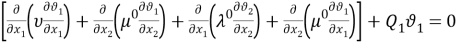
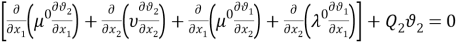
Построим интегральное тождество, которому должно удовлетворять обобщенное решение задачи (1).

Пусть произвольная функция из . Умножим первое уровнение системы (1) на и проинтегрируем по области

.

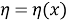
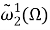
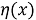
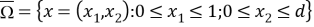
Используя формулу интегрирования по частям, найдем

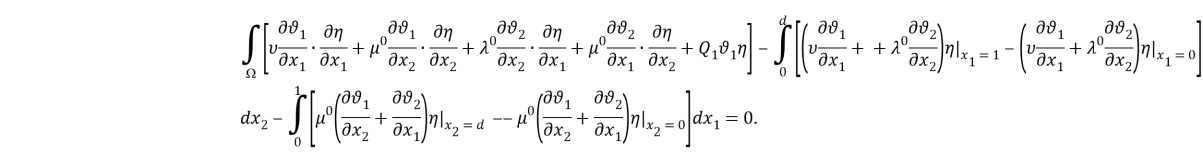
Учтем граничные условия (10)-(12) в [1]. Окончательно получим

. (2)

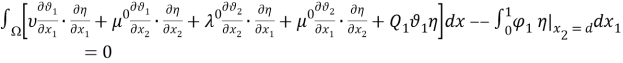
Для второго уравнения системы (1) аналогично будем иметь

(3)

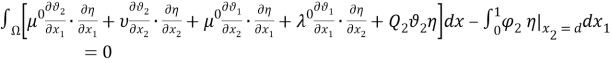
В области введем прямоугольную неравномерную сетку где

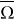
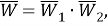
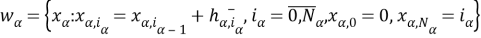
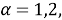
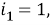
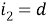
Пусть ; ,

; ; .

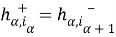
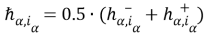
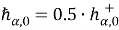
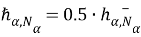
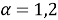
Обозначим через W множество всех внутренных узлов сетки ; узлы сетки при фиксированном ;

состоит из узлов при данном

— множество состоящее из и узла ;

включает и ; .

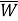
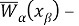
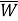
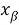
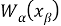
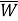
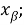
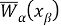
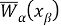
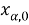
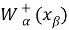
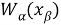
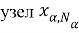
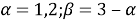
Считаем, что узлы сетки попадают на границы областей и .

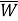
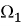
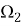
В тех случаях, когда не будет возникат недоразумений, вторые индексы при ; ; ; будем опускать и писать соответственно , , . Здесь и в дальнейшем используются обозначения, принятие в теории разностных схем [2, 3].

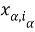
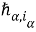
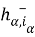
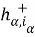
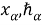
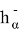
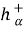
Систему интегральных тождеств (2), (3) аппроксимируем суммарными тождествами путем замены интегралов квадратурными формулами трапеций и центральных прямоугольников, а производных — разностными отношениями [2]. Получим систему:

; (4)

;

, .

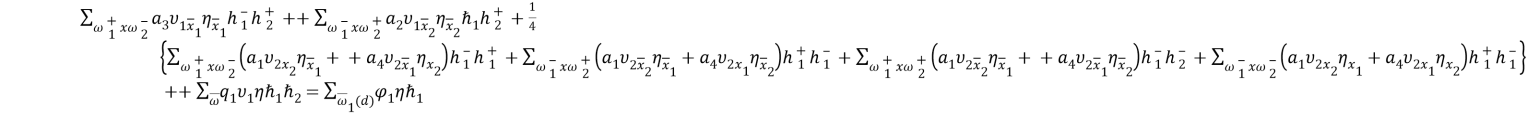
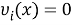
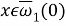
В тождествах (4) используются обозначения

;

;

;

;

;

;

.

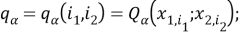
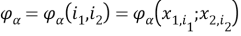
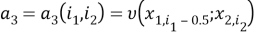
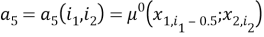
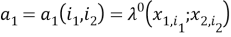
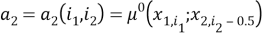
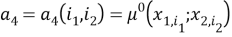
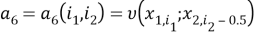
Приближенным решением задач (1)-(14) в [1] будем называть такую заданную на сеточную функцию V, которая при любой функции , определенной на той же сетке и равной нулю при , удовлетворяет сумматорным тождествам (4), где V-разностный аналог вектора упругих перемещений с компонентами и , соответствующими проекциям перемещений и на оси и .

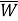
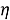
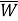
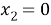
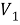
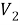
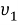
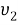
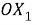
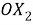
В силу произвольности функции положим её равной в одном из узлов сетки и равной нулю в остальных узлах. Перебирая таким образом все узлы, получим следующую разностную схему:

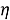
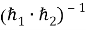
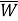
• внутренние узлы ( :

— — =0,

— — =0.

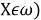
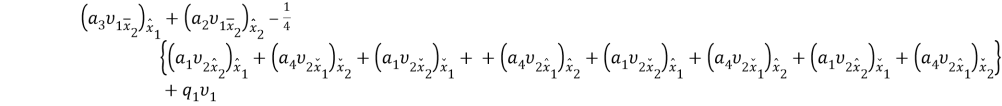
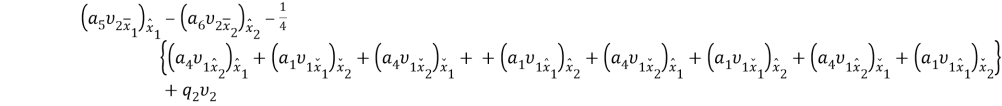
• граничные узлы:

:

— =0,

— =0.

:

— ;

— ;

:

— ;

— .

: .

• гловые точки:

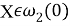
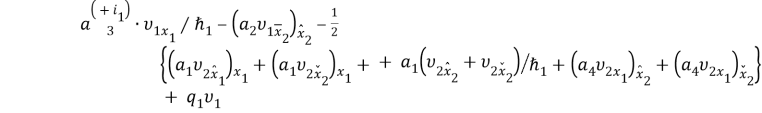
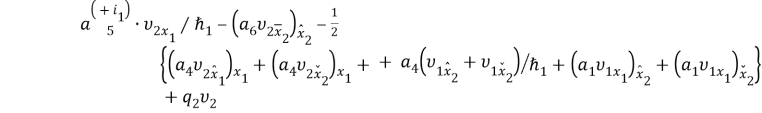
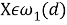
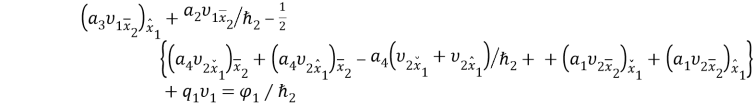
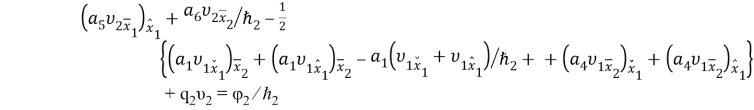
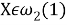
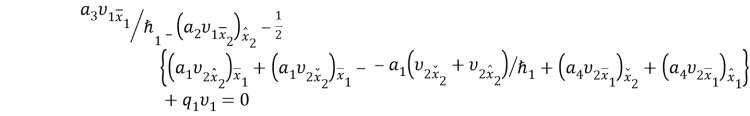
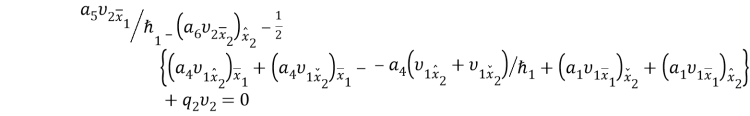
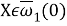
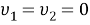
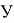
X=(0, :

— ;

— .

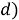
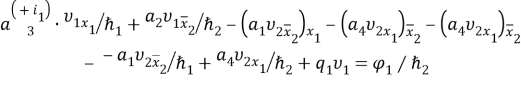
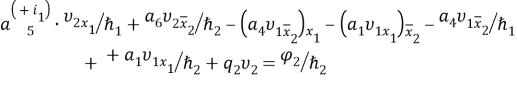
X=(1, :

— ;

— .

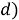
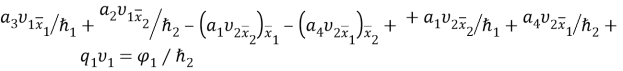
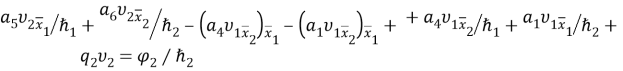
Здесь = .

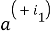
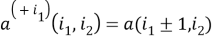
Литература:

1. Международный научный журнал «Молодой ученый» № 44 (431), ноябрь 2023
2. Самарский А. А., Андреев В. Д. Разностные методы для эллиптических уравнений — М.: Наука, 1976.
3. Самарский А. А. Николаев Е. С. Методы решений сеточных уравнений — М.: Наука, 1978.