В статье рассматривается задача об обслуживании клиентов в магазине и вычисляются некоторые показатели эффективности работы.

Ключевые слова: обслуживание, простейший поток, экспоненциальное распределение.

Рассмотрим такую задачу:

Допустим, что в магазине работает n касс. Число клиентов магазина представляет из себя простейший поток интенсивностью в человек в час. Допустим, что обслуживание представляет из себя экспоненциальное распределение. 1 клиент в среднем обслуживается за минут. Надо проанализировать длительность очереди клиентов, среднее время ожидания в очереди, среднее количество всех клиентов, обслуживаемых за это время.

Эта проблема очень распространена в сфере услуг. В результате данного анализа мы сможем приблизительно понять, сколько нужно кассовых аппаратов и, следовательно, сколько сотрудников.

Простейший поток и экспоненциальное распределение не выбрано случайным образом, а многие результаты схожи к показателям исследований. Более подробно об этих распределениях и их свойствах написано в [1].

Так как простейший поток представляет из себя Пуасонское распределиние, функция распределения будет:

,

где - вероятность, что в промежуток t в систему придут k клиентов.

Экспоненциальное распределение представляет из себя случайную величину , для которого

,

где , - среднее время обслуживания клиентов.

Обозначим вероятностью, что в промежутке t будет k клиентов. В [2] доказано, что удовлетворяет следующее рекурсивное соотношение:

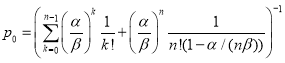
где условие значит, что количество приходяших клиентов меньше, чем количество клиентов, которых уже обслужили за одинаковый промежуток времени. В противном случае количество клиентов, стоящих в очереди, будет постоянно расти.

Выведем некоторые показатели эффективности:

– Вероятность того, что не будет не одного клиента будет.

– Вероятность того, что обслуживаются клиентов, будет .

– Вераятность того, что все кассы заняты обслуживая клиентов будет:

Отсюда получаем, что:

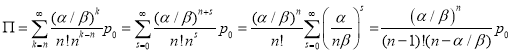
и для среднего времени ожидания получаем:

Среднее время пребывания клиента в магазине L будет равно:

Последная формула очевидна, поскольку присутствие в магазине означает, что клиент либо ждет в очереди, либо обслуживается.

Для получения средней длительности очереди клиентов рассмотрим случайную величину , которая представляет из себя возможную длину очереди. Очевидно, что — дискретная случайная величина, и поэтому функция распределения будет иметь такую форму:

Среднее значение длительности очереди A будет математическим ожиданием распределения (хи). Поэтому:

Вычислим полученную сумму:

,

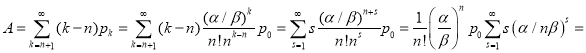
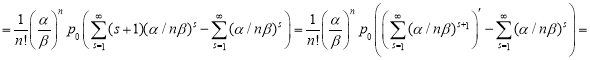
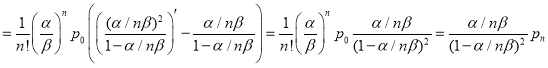где.

Вычислим среднее количество всех клиентов, обслуживаемых за это время B. Для получения значения B рассмотрим случайную величину , которая представляет из себя возможную длину очереди. Очевидно, что это дискретная случайная величина, и поэтому функция распределения будет иметь такую форму:

Среднее значение B будет равно:

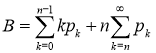
Идентично предыдущей схеме получим:

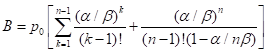
Есть ещё много второстeпенных показателей. Например, среднее количество клиентов, которое будет равно A + B.

Рассмотрим пример.

Допустим, что количество посетителей представляет из себя простейший поток интенсивностью 90 человек в час. Обслуживание представляет из себя экспоненциальное распределение. 1 клиент в среднем обслуживается за 1 минуту. Найдем минимальное количество касс, необходимых для корректной работы магазина, и вычислим показатели эффективности.

По нашим обозначениям .

Для начала допустим, что количество касс . В случае , означает, что кассы не успеют обслужить клиентов. Видно, что если то. Это означает, что при количестве 2 или более касс магазин успеет обслужить поток клиентов. Теперь вычислим показатели эффективности, когда .

В этом случае:

– ;

– ;

– ;

– ;

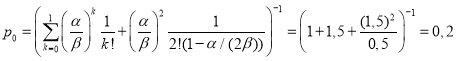
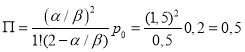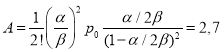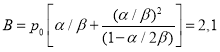– (= 120 сек․);

Исходя из результатов видно, что при касс магазин сможет обслужить своих клиентов, но будет очередь ().

Если рассмотрим вариант с тремя кассами (), то длина очерeди A будет равна:

,

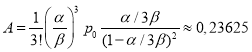что означает, что в среднем в очереди не будет даже одного клиента. Очевидно, что задействовать 4 кассы не имеет смысла, так как эта касса в среднем не будет обслуживать даже одного клиента.

Заключение:

Мы получили основные показатели эффективности обслуживания.

Литература:

1. Вентцель Е.С Теория вероятностей, Москва, 1969 г
2. Матвеев В. Ф., Ушаков В. Г. Системы массового обслуживания, Москва 1984 г