В статье рассмотрен процесс движения траектории точки кривой сателлита гибкого эпи-гипоциклоидального планетарного механизма в рабочей зоне сбора хлопка-сырца вертикальными шпинделями и в холостом зоне при съеме хлопка-сырца.

Ключевые слова: сателлит, водила, механизм, эпициклоида, гипоциклоида, передача, привод, ремень, кинематика.

Актуальность проблемы — несмотря на совершенствование конструкций хлопкоуборочных машин, ряд узлов и их деталей уменьшается их надежность, вследствие прогрессирующего износа ремней привода, поэтому вследствие изнашивания, этих ремней приводит к снижению агротехнических показателей машин [1].

Целью исследований является изучение условий работы привода шпинделей с разработкой математической модели их для построения траектории движения точки сателлита для обоих зон гибкого эпи-гипоциклоидального планетарного механизма.

Методика исследований включает теоретические вопросы кинематики движения сателлита в зонах сбора и съема их в камере уборочного аппарата и разработку математической модели их для эпи-гипоциклоидального планетарного механизма.

Основным узлом хлопкоуборочных машин являются уборочные аппараты, состоящие из вертикально-расположенных барабанов, содержащих по своей периферии, в специальных гнездах, вертикально размещенные шпиндели с приводными роликами, взаимодействующими с механизмами их прямого и обратного вращения. При движении хлопкоуборочной машины кусты 5 хлопчатника попадают в рабочую камеру, (рисунок 1, а) где контактируются со шпиндельными барабанами 6. В рабочей камере кусты 5 хлопчатника сжимаются с двух сторон барабанами 6 и, вращающиеся шпиндели 1 с посредством привода ремня 2 прямого вращения захватывают хлопок-сырец, извлекают его из коробочек 5 и наматывают на себя. При дальнейшем вращении шпиндельного барабана 6 хлопок-сырец совместно со шпинделями 1 переносится в зону съема 3, где направление их вращения меняется на противоположное, и хлопок-сырец со шпинделя частично снимаются самосбросом, а частично съемниками 4 подается в приемную камеру, откуда воздушным потоком через вентилятор попадает в бункер машины.

Задачей кинематического исследования является определение траектории перемещения, их скорости и ускорений точек движения звеньев сателлита гибкого планетарного механизма. Кинематические исследования можно вести аналитическим, графическим и графоаналитическими методами. При первом методе разрабатывается математическая модель в виде составления параметрических уравнений при движении точки сателлита в планетарной плоскости.

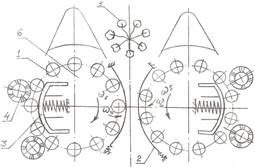
а)                              б)

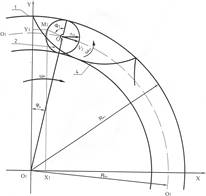
Рис. 1. Кинематическая схема (а) эпи-гипоциклоидального планетарного механизма и траектории движения сателлита в координатной оси 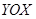 (б)

Для определения движений траекторий точки сателлита планетарного механизма обозначим: радиус водила через 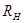, радиус сателлита — 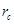, угол поворота водила — 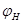, угол поворота сателлита по внутренней части ременной передачи — 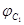, угла поворота сателлита по наружной части ременной передачи — 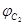. Спроектировав соответствующие радиусы звеньев механизма на выбранные координатные оси  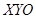(рисунок 1, б), получим параметрическое уравнение траектории движении точки сателлита:

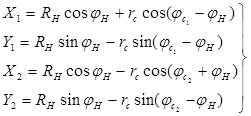                                                                        (1)

По вышеприведенным данным: 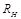, , 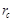, , 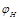 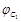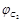напишем равенство: 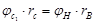, также 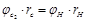, обозначив через передаточное отношение радиусов  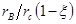ременной передачи будем иметь 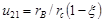, где 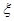 — коэффициент относительного скольжения в зависимости от типа ремня, 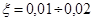;  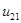— передаточное отношение радиуса  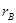внутренней части ременной передачи относительно радиуса  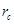сателлита.

Подставляя получим 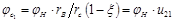. Также, обозначив через передаточное отношения в зоне наружной части передачи 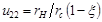, получим: 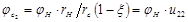, где 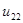 — передаточное отношение радиуса  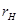наружной части ременной передачи относительно радиуса  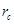сателлита в зоне эпициклоидального планетарного механизма.

Подставив полученные значения 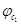 и 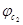 в выражение (1) получим:

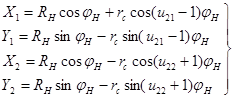                                                                            (2)

Преобразуем систему (2) и перепишем через передаточные отношения 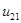,  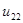ременной передачи, тогда в безразмерном виде получим:

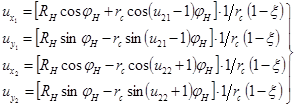                                                             (3)

Подставляя в уравнение (1) различные числовые значения 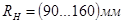 с шагом 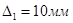,  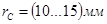с шагом  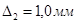и угла поворота водила  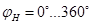с интервалом 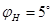, и используя прикладные пакеты AutoCAD, можно получить график кривых эпи-гипоциклоидальных траекторий движения точки сателлита. На рисунке 2 при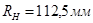 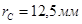  и угла поворота водила  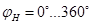с интервалом  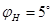получен график кривой эпициклоидальной (II) и гипоциклоидальной (I) траектории движения точки сателлита в рабочей зоне сбора хлопка-сырца и в зоне съема хлопка-сырца уборочного аппарата. Также в переходных зонах гибкого эпи-гипоциклоидального планетарного механизма получены дополнительно две совмещенные кривые (III) и (IV). Так, при переходе точки сателлита из эпициклоидальной (II) зоны в гипоциклоидальную (I) зону получена траектория движения точки сателлита, совмещенная с эпи-гипоциклоидальной (III) кривой, а в другой переходной зоне между гипоциклоидальной (I) и эпициклоидальной (II) также получена траектория движения совмещенной гипо-эпициклоидальной (IV) кривой планетарного механизма. Гипоциклоидальная кривая (I) получена в зоне прямого вращения шпинделя уборочного аппарата и является траекторией движения точки сателлита-шпинделя в рабочей зоне сбора хлопка-сырца, а эпициклоидальная кривая (II) обратного вращения шпинделя является траекторией движения точки сателлита в зоне съема хлопка-сырца.

Из рисунка 2 видно, что при вращении водила с угловой скоростью 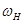 по часовой стрелки ролика шпинделя при соприкосновении его с ремнями прямого вращения получена гипоциклоидальная кривая (1) в четырех петлях, а в зоне обратного вращения при зоне съема хлопка-сырца получена эпициклоидальная кривая (II) в трех петлях. Габаритные размеры петли эпи-гипоциклоидальной кривой имеют два параметра: длину пути  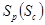и ширину. Длина пути  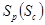петли эпи-гипоциклоидальной кривой имеет кратчайшее расстояние между выбранным по вершинам двух заостренной части точки гипоциклоиды (эпициклоиды) и составляет 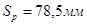, а ширина петли равно диаметру  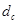сателлита, .

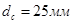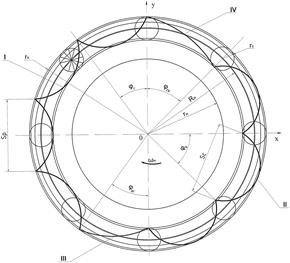
Рис. 2. Характер движения траектории точки кривой сателлита планетарного механизма в рабочей (I), съемной (II) и в переходных (III) (IV) зонах

Угол образования петли у гипоциклоидальной кривой составляет 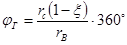, а у эпициклоиды 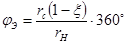. Подставляя численные значения получим: 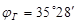; 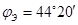, следовательно угол рабочего сбора хлопка-сырца шпинделем составляет 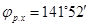, а угол в зоне съема хлопка-сырца .

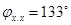На основании проведенного исследования можно сделать следующие выводы:

1.         Проведена и составлена математическая модель кинематики движения сателлита-шпинделя гибкого эпи-гипоциклоидального планетарного механизма для рабочего органа привода шпинделей уборочного аппарата в рабочей и съемной зоне сбора хлопка-сырца.

2.         При кинематическом исследовании получены аналитические выражения в размерных и безразмерных величинах и выявлен в графическом виде характер движения траектории кривой точки сателлита планетарного механизма в рабочей и съемной зоне хлопка-сырца.

Литература:

1.         Алимова Д. Б. К вопросу применения гибкого эпи-гипоциклоидального планетарного механизма для привода шпинделей хлопкоуборочной машины. // Республиканская научно-практическая конференция молодых ученых. Ташкент 14–16 мая, 2014 й. — С. 71–75.