В статье исследуется проблема формирования у студентов навыков математического моделирования процесса принятия решений в профессионально ориентированных задачах бизнес-планирования и эффективного управления.

Ключевые слова: математические модели, анализ деловых ситуаций, применяются математические задачи, решение задач бизнес-планирования.

Abstract. The article is devoted to the problem of developing of students' skills of mathematical modeling of decision-making process in the problems of business planning and effective management.

Keywords: mathematical models, analysis of business situations, applied mathematical problems, solution of business planning problems.

Согласно новому закону об образовании в России высшее образование призвано обеспечить подготовку высококвалифицированных кадров в соответствии с потребностями общества и государства, удовлетворение потребностей личности в интеллектуальном развитии, углублении и расширении образования. Поставленная цель предполагает решение целого ряда задач, одной из которых является обновление содержания высшего профессионального образования, в связи с чем актуализируются вопросы методики преподавания дисциплин и информационно-методического обеспечения образовательного процесса.

Современный преподаватель вуза сталкивается с проблемой структурирования, психологически грамотного и методически оправданного преобразования научного знания и профессионально–ориентированного материала в учебный материал.

Так, целью изучения математических дисциплин программ бакалавриата направлений экономического профиля является формирование методологии экономико-математического моделирования социально-экономических процессов, а также практических навыков использования экономико-математических методов для принятия эффективных управленческих решений и их экономического анализа.

Достижение названной цели предполагает формирование соответствующих компетенций, компоненты которых включают

– знание базовых экономико-математических моделей, предназначенных для решения типовых оптимизационных задач планирования и управления;

– умение разработать постановку задачи оптимального планирования и управления социально-экономическим процессом, сформировать на ее основе экономико-математическую модель, выбрать метод и средства для решения задачи, дать экономическую интерпретацию результатов.

Для анализа, прогнозирования и выбора оптимальных бизнес-стратегий при планировании и оперативном управлении производством; управлении трудовыми ресурсами; запасами; распределении ресурсов; размещении объектов; руководстве проектом; распределении инвестиций и т.п. необходимым инструментом являются математические модели. Как известно, экономико-математические модели – это модели, описывающие экономические процессы, объекты, связи с использованием математического аппарата: функций, уравнений, неравенств, их систем.

Обучение решению проблем эффективного управления бизнесом, расчета прибыли предпринимательской деятельности и себестоимости производимых товаров и услуг, необходимые для успешной конкуренции, происходит при формировании у студентов умений математического моделирования процесса принятия решения в задачах бизнес-планирования [1, 2, 3].

Под бизнес-планированием принято понимать процесс описания и прогнозирования планируемых действий в бизнесе, а также анализ вероятности наступления желаемых событий и появления желаемых результатов. Решения, которые принимаются в реальных производственных условиях (распределение ресурсов, управления поставками, организации перевозок и т.д.), связаны с переработкой огромных массивов информации, и зависят также от воздействия различных случайных факторов. Возникает необходимость в рациональном анализе и описании бизнес-ситуаций.

Рассмотрим анализ бизнес-ситуации, переход к прикладной задаче и построению ее математической модели на примере.

Бизнес-ситуация 1. Предоставляется выбор временной работы по сбыту в двух местах. Оплата работы на первом месте основывается на комиссионных началах: доход зависит от того, сколько вам удалось продать. Здесь имеются два в равной степени вероятных дохода: 2000 ден. ед. при высокой продаже, 1000 – при средней. За большую часть времени на втором месте работы платят 1510 ден. ед., но вы можете получить 510 ден. ед. в виде выходного пособия, если фирма выходит из бизнеса. Как выбрать себе место работы?

Проведем анализ бизнес-ситуации: На первом месте имеется два в равной степени дохода, то есть из условия имеем: 2000 ден. ед. при высокой продаже с вероятностью равной 0,5; 1000 ден. ед. при средней продаже с вероятностью так же равной 0,5. На втором месте за большую часть времени платят 1510 ден. ед., вероятность наступления данного события будем считать равной 0,99, тогда в случае выхода фирмы из бизнеса, с вероятностью равной 0,01 можно получить 510 ден. ед.

Анализ бизнес-ситуации предполагает:

1) выделение информационных данных и определение условий бизнес-ситуации;

2) установление связей между информационными данными и формулировка прикладной задачи.

Если в течение достаточно долгого периода времени условия практически не меняются, то решение принимается в ситуации определенности. Если же на них существенно влияют некоторые случайные факторы, то решение принимается в условиях неопределенности, риска. Основным инструментом, с помощью которого можно свести нежелательный риск к минимуму являются вероятностные модели.

Сформулируем прикладную задачу.  Найти среднеожидаемые значения зарплаты на первом и втором месте, используя исходные данные. (Если они в обоих случаях окажутся приближенно равными, то критерием большего риска служит большее значение среднеквадратического отклонения).

Перейдем к моделированию задачи. Введем следующие случайные величины:

x – первое место работы;

y – второе место работы.

Законы распределения этих случайных величин приведены в таблице 1:

Таблица 1 – Распределение случайных величин

Расчет по модели.

Найдем математические ожидания (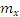, 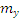) и среднеквадратические отклонения (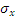, 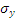) величин x и y, используя следующие формулы:

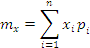
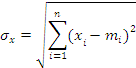
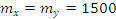
Итак, оба места работы имеют одинаковый ожидаемый доход. Далее найдем среднеквадратичное отклонение величин x и y. Они окажутся равными 501 и 99,8. Из этого сделаем вывод: второе место работы более предпочтительно с точки зрения риска, чем первое.

Бизнес-ситуация 2. Необходимо принять решение об инвестировании некоторого капитала в один из двух проектов:

– проект №1 сулит прибыль в размере 50 ден. ед. с вероятностью 0,4

– проект №2 сулит прибыль в размере 80 ден. ед. с вероятностью 0,2

Какому проекту отдать предпочтение как наиболее прибыльному?

Анализ бизнес ситуации. С вероятностью 0,4 проект №1 сулит прибыль 50 ден. ед., значит с вероятностью 0,6, прибыль будет равна 0 ден. ед. С вероятностью 0,2 проект №2 сулит прибыль 80 ден. ед., поэтому с вероятностью 0,8 прибыль составит 0 ден. ед.

Сформулируем прикладную задачу. Сравнить среднеожидаемую прибыль в случае выбора проекта №1 и №2.

Перейдем к моделированию задачи. Введем случайные величины:

x – характеризует прибыль проекта №1;

y – характеризует прибыль проекта №2.

Законы распределения этих случайных величин приведены в таблице 2:

Таблица 2 – Распределение случайных величин

Расчет по модели.

Найдем математические ожидания (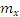, 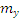) величин x и y по формуле:

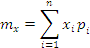
Математические ожидания данных случайных величин равны:

 ; ; .

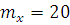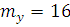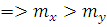Итак, стоит отдать предпочтение проекту №1 как наиболее прибыльному, исходя из среднеожидаемых результатов.

Таким образом, примеры демонстрируют следующую схему процесса формирования и принятия эффективного решения:

1) формулировка бизнес-ситуации;

2) анализ бизнес-ситуации;

3) формулировка прикладной задачи;

4) построение математической модели задачи;

5) расчеты по модели и их оценка;

6) формулировка решения.

Использование названной схемы позволяет преподавателю в реальном учебном процессе осуществлять информационно-методическую деятельность, включающую проектирование и разработку профессионально–ориентированных упражнений, тестов по различным темам и форм их представления в соответствии с современными требованиями [4, 5].

Литература:

1.      Атрощенко С.А. Формирование у учащихся базовых математических моделей задач эффективного управления // Международный научно-исследовательский журнал = Research Journal of International Studies. – 2013. – № 7-4 (14). – С. 55-56.

2.      Атрощенко С.А. Теория и методика обучения студентов педвуза методам изображения геометрических фигур в контексте укрупнения дидактических единиц: дисс. на соиск. уч. степени канд. пед. наук. – Арзамас, 1998.  – 186 с.

3.      Лысенкер В.Л., Лысенкер Л.Ш. Математика и бизнес. – М.: ИЛЕКСА, 2011. – 77 с.

4.      Напалков С. В. Электронные образовательные тренажёры по математике как эффективное средство развития познавательной активности сельских школьников // Мир науки, культуры, образования. – 2012. – № 1(32). – С. 98-101.

5.      Первушкина Е.А. Модель развития геометрической креативности школьников при обучении математике в 5-6 классах с использованием информационных технологий // Школа будущего. – 2011. – № 6. – С. 58-64.