Рассматриваются средства формирования профессиональных умений бакалавров по направлению “Строительство” на занятиях по математике.

Ключевые слова: профессиональная деятельность, профессиональные умения, профессионально-ориентированная математическая задача.

Связь образования с будущей профессией выпускника всегда была актуальной проблемой образования. Подобная тематика поднималась в трудах многих ученых, но была недостаточно отражена в стандартах 2 поколения, особенно для непрофильных дисциплин. Этот недостаток был устранен с введением ФГОС — 3. При изучении математики, в соответствии с новым стандартом бакалавр по направлению 270800 “Строительство” должен: знать фундаментальные основы высшей математики, включая алгебру, геометрию, математический анализ, теорию вероятностей и основы математической статистики; уметь самостоятельно использовать математический аппарат, содержащийся в литературе по строительным наукам, расширять свои математические познания; владеть первичными навыками и основными методами решения математических задач из общеинженерных и специальных дисциплин профилизации. [1].

Реализация требований, предъявляемых новыми образовательными стандартами к бакалавру, на наш взгляд возможна путем формирования и развития профессиональных качеств личности обучаемого.

Развитие профессиональных качеств личности предполагает, прежде всего, формирование умений, отражающих специфику профессиональной деятельности бакалавра — строителя. В свою очередь, профессиональную деятельность бакалавра — строителя можно подразделить на проектно — конструкторскую, организационно — управленческую, производственно — технологическую, исследовательскую. Каждый из видов профессиональной деятельности характеризуется совокупностью умений, которыми должен владеть специалист при решении профессиональных задач. Немаловажную роль в формировании этих умений играет дисциплина математика. Проанализировав государственный образовательных стандарт ФГОС ВПО по направлению 270800 “Строительство” мы выделили ряд умений, которые необходимо и возможно формировать у специалиста данного профиля средствами математики [2,3].

Выделим ряд профессиональных умений, адекватных основным видам профессиональной деятельности:

-          проектно–конструкторские — умение использовать математические средства в проведении инженерных и инженерно–экономических исследований и разработок при проектировании и сооружении объектов строительства;

-          организационно–управленческие — умение использовать математический аппарат при составлении отчетов, планов, смет и т. д.; умение, используя математические методы, принимать оптимальные управленческие решения; умение проводить экспертизу и оценку строительных объектов математическими средствами;

-          производственно-технологические — умение осуществлять математические расчеты при возведении, ремонте и реконструкции зданий и сооружений;

умение на основе использования математических методов находить оптимальные решения при сооружении строительных конструкций;

-                   исследовательские -- умение с использованием средств математики выполнять экспериментальные и теоретические исследования в области строительства и в других отраслях, связанных со строительством (умение определять распределение температурно-влажностных характеристик в строительных материалах и сооружениях математическими методами; умение с помощью математических средств исследовать эффективность работы механизмов строительных машин; умение производить математические расчеты на выявление прочности, устойчивости, деформации элементов строительных конструкций и целых сооружений; умение применять математический аппарат при вычислении скорости протекания строительных процессов; умение производить математическую обработку экспериментальных данных); умение разрабатывать рекомендации и делать выводы о явлении на основе проведенных математических исследований строительных объектов и процессов.

Развитие перечисленных умений возможно осуществить посредством решения профессионально-ориентированных математических задач.

Под профессионально ориентированной математической задачей мы понимаем задачу, условие и требование которой определяют собой модель некоторой ситуации, возникающей в профессиональной деятельности бакалавра-строителя, а исследование этой ситуации средствами математики способствует профессиональному развитию личности специалиста.

Профессионально ориентированные задачи, используемые в рамках математической подготовки бакалавра-строителя, должны удовлетворять следующим требованиям:

1)      задача должна описывать ситуацию, возникающую в профессиональной деятельности бакалавра-строителя;

2)      в задаче должны быть неизвестны характеристики некоторого профессионального объекта или явления, которые надо исследовать субъекту по имеющимся известным характеристикам с помощью средств математики;

3)      решение задач должно способствовать прочному усвоению математических знаний, приемов и методов, являющихся основой профессиональной деятельности бакалавра-строителя;

4)      задачи должны обеспечить усвоение взаимосвязи математики с общетехническими и специальными дисциплинами;

5)      содержание задачи и ее решение требуют знаний по специальным предметам;

6)      содержание профессионально ориентированной математической задачи определяет пропедевтический этап изучения понятий специальных дисциплин;

7)      решение задач должно обеспечивать математическое и профессиональное развитие личности бакалавра-строителя.

Профессионально ориентированные математические задачи можно проклассифицировать согласно видам профессиональной деятельности бакалавра-строителя: проектно-конструкторские, организационно — управленческие, производственно-технологические, исследовательские.

Проектно-конструкторские задачи — это задачи, отражающие применение математических средств при проведении инженерных и инженерно-экономических исследований специалиста в области проектирования объектов строительства.

Приведем пример подобной задачи: необходимо спроектировать план застройки массива десятью домами, причем домов первого типа должно быть три, второго типа — пять, третьего типа — два. Сколько вариантов плана можно представить?

Организационно-управленческие задачи касаются вопросов, связанных с использованием математического аппарата в процессе подготовки производственных отчетов, принятия управленческих решений, осуществления контроля за производством и качеством строительных объектов.

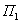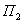Например: завод ЖБИ выпускает декоративные плиты двух типоразмеров —  и , затрачивая цветные минеральные наполнители (ЦМН) и цветные минеральные заполнители (ЦМЗ), единовременные ресурсы которых ограничены; доход от реализации продукци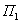и  и 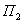 различен. Данные представлены в таблице 1.

Таблица 1

Расход и ресурсы материалов

Необходимо найти объем производимых плит, чтобы доход завода был максимален.

Производственно-технологические задачи демонстрируют применение математических знаний при возведении, ремонте и реконструкции зданий, сооружений и строительных конструкций [2,4,5].

В качестве примера приведем следующую задачу: для придания консоли 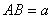 жесткости используются две опоры  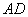и 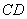, представленные на рисунке 1, где .

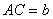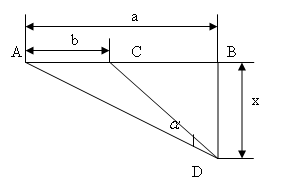
Рис. 1 Схема опирания консоли

Наибольшая жесткость конструкции достигается при наибольшей величине угла 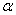, тангенс которого определяется формулой: 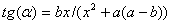. Определите, на каком расстоянии от точки  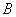следует закрепить опоры, чтобы придать конструкции наибольшую жесткость.

Исследовательские задачи связаны с использованием математических методов при выполнении экспериментальных и теоретических исследований в области строительства и других отраслей, связанных со строительством.

Примером задачи этого типа может служить такая задача: по опытным данным зависимости водопоглощения 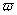от температуры обжига Т, приведенным в таблице 2, определить водопоглощение для промежуточного значения Т=1250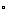С.

Таблица 2

Зависимость водопоглощения от температуры обжига

Приведенные задачи, на наш взгляд, позволят сформировать у будущего выпускника необходимые умения, которые в дальнейшем будут способствовать успешному применению математики в профессиональной деятельности.

Литература:

1.      Федеральный государственный образовательный стандарт высшего профессионального образования по направлению подготовки 270800 Строительство (квалификация (степень) «бакалавр») / Министерство образования и науки Рос. Федерации., 2010.

2.      Бочкарева О. В., Профессиональная направленность обучения математике студентов инженерно-строительных специальностей вуза [Текст]: автореферат диссертации кандидата технических наук / О. В. Бочкарева — Пенза, 2006–18 с.

3.      Снежкина О. В., О роли регионального компонента при преподавании дисциплин математического цикла/ О. В. Снежкина, Г. А. Левова, О. В. Бочкарева, Р. А. Ладин // Новый университет № 11–12 (32–33). 2013.-С.17–21.

4.      Ладин Р. А., Математика и междисциплинарные связи / Р. А. Ладин, О. В. Снежкина, О. В. Бочкарева, Н. В. Титова //Молодой ученый. № 1 (60).Часть 4. 2014.-С.550–553.

5.      Ямбогло И. И., Некоторые аспекты обучения иностранных студентов в российских вузах / И. И. Ямбогло, О. В. Бочкарева, О. В. Снежкина // Вестник магистратуры. № 1(28).2014.-С.25–28.
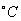
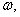