В данной работе рассматривается задача о воздействии течения, создаваемого источником, на распространение поверхностных волн. Указывается теоретическая возможность полного гашения волн подбором соответствующих характеристик источника.
Ключевые слова: поверхностные волны, гашение, источник.
Рассмотрим плоское потенциальное движение идеальной несжимаемой жидкости, ограниченной сверху свободной поверхностью, снизу – непроницаемым дном. Исследуем изменение интенсивности исходного волнения за счет создания течения от источника, помещенного под свободной поверхностью на пути распространения волн. Известно [1], что эта задача – нелинейна. Для получения решения в замкнутой форме будем рассматривать ее учетом традиционной линеаризации.
1. Постановка задачи. Требуется найти потенциал скорости 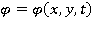 , удовлетворяющий уравнению Лапласа
, удовлетворяющий уравнению Лапласа
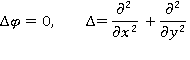
и краевым условиям:
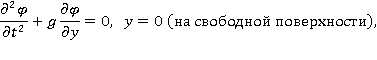
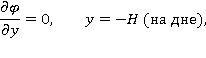
а также некоторым условиям на бесконечности, которые будут указаны ниже. Здесь ось  направлена вдоль невозмущенного уровня свободной поверхности вправо, ось
направлена вдоль невозмущенного уровня свободной поверхности вправо, ось 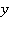 – вертикально вверх;
– вертикально вверх; 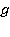 – ускорение свободного падения;
– ускорение свободного падения; 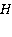 – глубина жидкости.
– глубина жидкости.
Ордината свободной поверхности определяется выражением [1]:
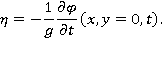
Для дальнейшего положим:
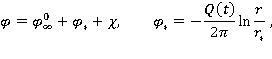
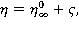
где 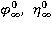 – потенциал скорости и ордината свободной поверхности исходного волнения;
– потенциал скорости и ордината свободной поверхности исходного волнения; 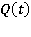 – интенсивность источника;
– интенсивность источника; 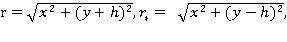
 - величина заглубления источника;
- величина заглубления источника; 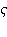 – возмущенная часть свободной поверхности. Поставим и условия на бесконечности:
– возмущенная часть свободной поверхности. Поставим и условия на бесконечности:
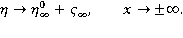
Пусть
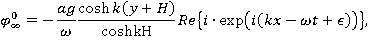
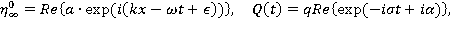
где 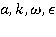 – амплитуда, волновое число, частота и фаза исходных волн;
– амплитуда, волновое число, частота и фаза исходных волн; 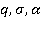 – амплитуда, частота и фаза колебаний источника. Положим [2]
– амплитуда, частота и фаза колебаний источника. Положим [2]
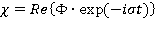
и сформулируем задачу для 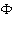 :
:
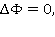
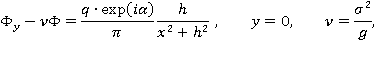
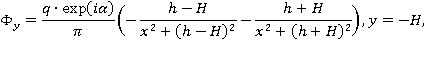
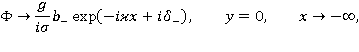
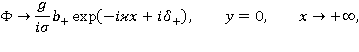
где величины 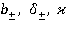 - искомые.
- искомые.
Поставленная задача определяет потенциал скорости при волнообразовании от источника. Это решение симметрично по  относительно
относительно 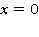 .
.
2. Решение поставленной задачи. Приведем краткое изложение метода, предложенного Л. Н. Сретенским[1], с использованием прямого пути построения решения.
В силу свойства симметрии решения, гармоническую функцию 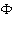 представим в виде:
представим в виде:
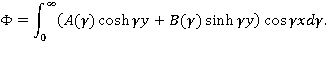
Удовлетворяя граничным условиям, получаем:
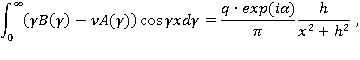
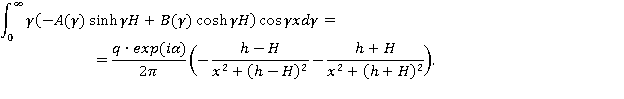
Отсюда, применяя свойства интеграла Фурье и пользуясь равенством
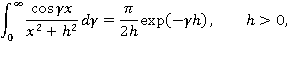
получаем
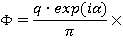
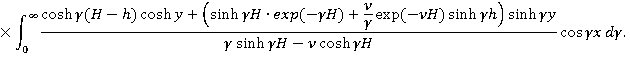
Ордината свободной поверхности определяется выражением:
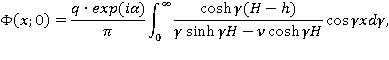
в котором подынтегральная функция обращается в бесконечность при
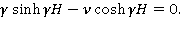
Корнями этого уравнения являются:
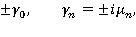
причем 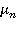 есть корень уравнения
есть корень уравнения
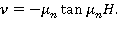
В этом случае предыдущий интеграл следует понимать в смысле главного значения по Коши [3].
Вычислим его. Представим
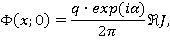
где
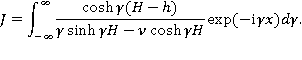
Продолжим аналитически подынтегральную функцию на область плоскости комплексного переменного 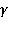 , ограниченную сверху полуокружностью
, ограниченную сверху полуокружностью 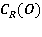 , снизу – отрезками вещественной оси
, снизу – отрезками вещественной оси 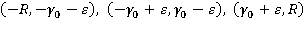 и полуокружностями
и полуокружностями 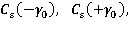 расположенными ниже вещественной оси. Согласно теореме Коши [3], интеграл от аналитической функции
расположенными ниже вещественной оси. Согласно теореме Коши [3], интеграл от аналитической функции
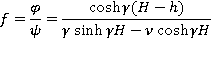
по указанному контуру будет равен 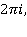 умноженному на сумму вычетов в точках
умноженному на сумму вычетов в точках 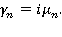
Отсюда получаем после перехода к пределу при 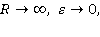 что
что
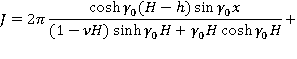
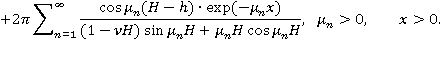
Следовательно
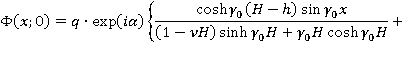
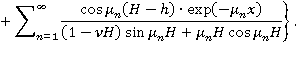
Чтобы удовлетворить условиям на бесконечности, надо к полученному частному решению неоднородной задачи присоединить решение однородной задачи:
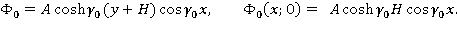
При этом:
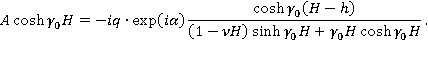
Тогда будем иметь:
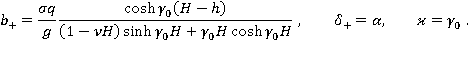
Итак, ордината свободной поверхности при больших  принимает вид:
принимает вид:
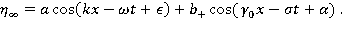
Пусть 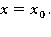 Найдем
Найдем 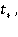 доставляющее максимум величины
доставляющее максимум величины 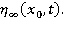 Затем следует подобрать параметры
Затем следует подобрать параметры 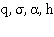 с тем, чтобы минимизировать
с тем, чтобы минимизировать 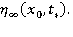 В общем случае
В общем случае 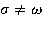 максимум выражения для ординаты свободной поверхности по
максимум выражения для ординаты свободной поверхности по  находится численным решением трансцендентного уравнения; последующая минимизация также осуществляется численно.
находится численным решением трансцендентного уравнения; последующая минимизация также осуществляется численно.
3. Частный случай. В случае 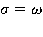 получается аналитическое решение задачи. Тогда:
получается аналитическое решение задачи. Тогда:
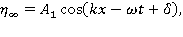
где
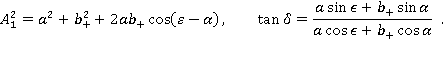
Таким образом, амплитуда прошедшей волны явно выражается через параметры источника. Нетрудно видеть в этом случае, что минимум выражения для амплитуды прошедшей волны достигается при 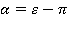 и равен
и равен 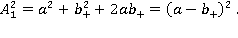
Отсюда, проходящая волна исчезает при 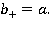 Подставляя это условие в выражение для амплитуды проходящей волны, получаем необходимую величину расхода источника, находящегося на глубине
Подставляя это условие в выражение для амплитуды проходящей волны, получаем необходимую величину расхода источника, находящегося на глубине  :
:
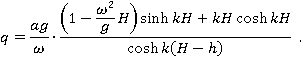
Литература:
1. Сретенский Л.Н. Теория волновых движений жидкости. - М.: Наука, 1977.
2. Хаскинд М.Д. Гидродинамическая теория качки корабля. – М.: Наука, 1973.
3. Лаврентьев М.А., Шабат Б.В. Методы теории функций комплексного переменного. – Изд. 5-е, испр. – М.: Наука, 1987.

