Разнообразие теоретических исследований . Исследовались различные виды креативности: историческая и личностная креативность (М. Боден), коммуникативная креативность (Т. А. Барышева, Ю. А. Жигалов, В. П. Пархоменко), вербальная креативность (Л. Г. Алексеева, А. Н. Воронин), креативность как качество личности (С. Л. Рубинштейн, А. Маслоу, Д. Б. Богоявленская), креативность в дошкольном возрасте (Н. Н. Подъяков, Л. А. Вернер), креативность как психологическое свойство (Я. А. Пономарев).
Компоненты теории креативности. Р. Муни выделил понятия: креативный процесс, креативная личность, креативный продукт и креативная среда. Креативный процесс понимается как форма активности в проблемном поиске. Его целью является формирование креативных свойств субъекта. Значительная часть креативного процесса состоит в постепенной аккумуляции «точек роста» креативности и создании условий для возможного «скачка». В обобщенном виде креативный продукт представляется в виде достижения субъектом положительной динамики в усвоении знаний и развития на данном отрезке креативного процесса. Креативный процесс, креативные свойства субъекта и реально получаемый креативный продукт интерпретируются как компоненты, образующие креативную среду . Различные сочетания значений троек этих компонентов приводят к трехмерной дидактической модели креативной среды. По аналогии с развивающим обучением говорят о креативном обучении, о системах и технологиях креативного обучения [2]. Ввиду многообразия содержания понятия креативности, в психологии и педагогике креативность рассматривается как интегральная способность к творчеству, имеющаяся в наличии у человека в развитом виде или в потенциальной форме. Последнее особенно важно учитывать при организации развивающего обучения, включающего в себя креативное обучение учащихся.
Условия для проявления творческих качеств субъектов: создание креативной среды; раннее начало формирования креативных навыков в процессе обучения всем учебным предметам на основе применения синтетического метода поиска решения задач, анализов Паппа и Евклида; формирование креативных навыков [1]. На основе технологии креативного обучения трансформируется репродуктивная деятельность, приобретая инновационные качества (например, сообщение в готовом виде образцов поисковой деятельности, образцов применения эвристических приемов).
Технологическая модель креативного процесса обучения геометрии. Для успешности креативного обучения используем технологическую модель креативного процесса обучения геометрии [1, с. 119, таблица 1].
Таблица 1
Модель креативного процесса обучения геометрии (в сокращ. виде)
|
Этапы |
Характеристика креативной деятельности |
|
I. Встреча с информационным сообщением: проблемная ситуация-1 |
Осознание информационного сообщения, представляемого в какой-либо форме: вербальной, графической, символической. Высказывание гипотез о том, какие геометрические задачи или теоремы можно составить на основе данного информационного сообщения. |
|
II. Переход от проблемной ситуации-1 к формулированию геометрических задач |
Компоненты структуры задачи , характеризующие ее с позиции субъектного подхода, записываются нами словом АВRСМЭ, в котором: А — условие задачи; В — требование задачи; С — теоретический базис решения; R — основное отношение между данными и искомыми; М — математический метод решения (М⊂С); Э — эвристические средства решения |
|
III. Поиск решения геометрической задачи — начальный этап поиска: проблемная ситуация-2 |
Поисковая деятельность учащихся — основной компонент креативного процесса — учебная деятельность, направленная на усвоение новых знаний, новых способов действий с ними; способствующая развитию творческих качеств личности. Создаются поисковые ситуации, способствующие формированию креативного мышления . |
|
IV . Основной этап поиска решения геометрической задачи: проблемная ситуация-3 |
Проблемная ситуация связывается с применением конкретизирующей и разрешающей моделей (они отражают специфику учебной темы, конкретной задачи). Отличительной особенностью конкретизирующих поисковых моделей является формулирование их в конкретно-предметной форме, ориентированной на учебную тему, на конкретную задачу, на формирование навыков выделения основного отношения, признаков математических методов. |
|
V . Рефлексия и обобщение |
Записывается найденное решение. Проводится рефлексия и обобщение процесса поиска. |
Некоторые выводы. Креативность и развивающее обучение имеют много общего, но эти понятия не совпадают. Креативность рассматривается как высшая форма развития субъекта. Методики формирования креативности и развития во многом схожи. Различия проявляются в масштабах и интенсивности реализации. На наш взгляд, креативность предполагает более форсированное и систематичное её формирование, подталкивающее естественные процессы формирования. Можно сказать, что креативное обучение есть развивающее обучение, в его наиболее целенаправленной и интенсивной форме . В этом смысле креативное обучение может рассматриваться как часть, как разновидность развивающего обучения.
Организация поиска решения задачи. Сообщается, что существуют различные методы построения сечений тел (метод использования линий пересечения плоскостей несмежных граней, метод следа, метод использования свойств данного тела и секущей плоскости, метод внутреннего проектирования и др.). Знакомство с методами решений начнем с наиболее простого метода — метода использования линий пересечения плоскостей несмежных граней (рис. 1).
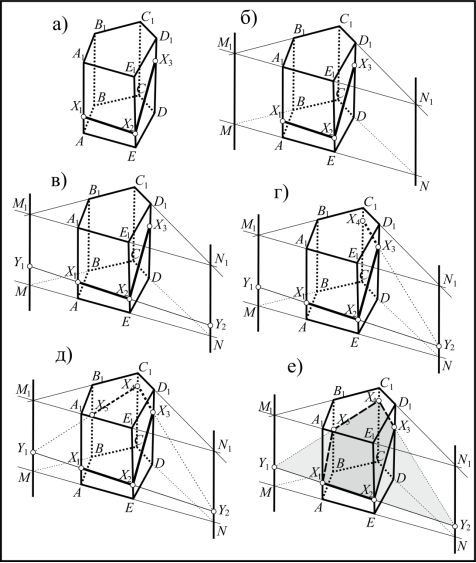
Рис. 1
Первоначальное знакомство с методом осуществляется в словесной форме, сопровождаемой визуальным сопровождением каждого шага построений.
Задача 1. Дана пятиугольная призма ABCDЕA 1 B 1 C 1 D 1 Е 1 , X 1 ∈ AA 1 , X 2 ∈ ЕЕ 1 , X 3 ∈ DD 1 . Постройте сечение призмы плоскостью X 1 X 2 X 3 (чертеж 1).
Шаг 1. Некоторые стороны многоугольника сечения можно построить сразу: строим стороны X 1 X 2 и X 2 X 3 (рис. 1а).
Шаг 2. Далее строим прямые пересечения MM 1 и NN 1 плоскостей несмежных боковых граней призмы — их применение лежит в основе замысла построения сечения. Для этого строим две точки этих прямых (рис. 1б, точки M,M 1 и N,N 1 ): М = АЕ ∩ ВС, M 1 = A 1 Е 1 ∩ В 1 C 1 ; N = AE ∩ CD, N 1 = A 1 Е 1 ∩ C 1 D 1 . Проводим прямые MM 1 и NN 1 : МM 1 = АA 1 Е 1 Е ∩ DD 1 C 1 C ; NN 1 = АA 1 Е 1 Е ∩ СС 1 D 1 D.
Шаг 3. Выясняем, какие вершины многоугольника сечения можно построить с помощью прямых MM 1 и NN 1 (рис. 1в). Замечаем, что прямая X 1 X 2 пересекает обе прямые МM 1 и NN 1 (все три прямые лежат в одной плоскости). Строим точки пересечения: Y 1 = X 1 X 2 ∩ MM 1 , Y 2 = X 1 X 2 ∩ NN 1 . Так как точка Y 1 принадлежит прямой MM 1 и прямая MM 1 принадлежит секущей плоскости, то точка Y 1 принадлежит секущей плоскости, аналогично: так как точка Y 2 принадлежит прямой NN 1 и прямая NN 1 принадлежит секущей плоскости, то точка Y 2 принадлежит секущей плоскости.
Шаг 4. Прямая Y 2 Х 3 принадлежит секущей плоскости (рис. 1г). Кроме того, эта прямая лежит в плоскости боковой грани СС 1 D 1 D . Поэтому прямая Y 2 Х 3 пересекает прямую СС 1 в некоторой точке Х 4 , которая является четвертой вершиной многоугольника сечения: Х 4 = Y 2 Х 3 ∩ СС 1 .
Шаг 5. Так как прямые Y 1 Х 4 и ВВ 1 принадлежит одной плоскости — плоскости боковой грани ВВ 1 С 1 (чертеж 1д), то можно построить точку их пересечения — точку Х 5 , которая является пятой вершиной многоугольника сечения: Х 5 = Y 2 Х 4 ∩ BB 1 . Таким образом, получаем искомое сечение Х 1 Х 2 Х 3 Х 4 Х 5 (рис. 1е).
Обобщающее коллективное закрепление.
- С каким методом построения сечений мы познакомились? Как он называется? Почему сразу можно построить стороны X 1 X 2 и X 2 X 3 (чертеж 1а)?
- Как строятся прямые МM 1 и NN 1 (чертеж 1б)?
- Использование прямых в дальнейшем начинается с построения точек Y 1 и Y 2 . Как они строятся?
- Как с помощью этих точек строятся две последние вершины многоугольника сечения? Какие именно вершины? Объясните, почему они действительно являются вершинами искомого многоугольника (чертеж 2).
- Какие вопросы возникли по решению задачи? Задайте их.
В качестве тренировки и выработки навыка обоснования предлагается следующая задача.
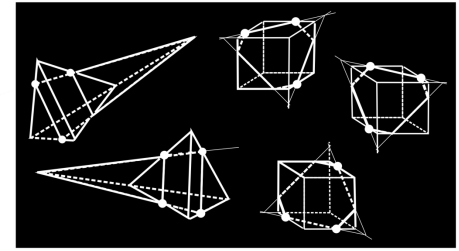
Рис. 2
Задача 2. На рис. 2 плоскость сечения задана тремя точками (они выделены светлыми кружочками). Укажите последовательность построений сечения и назовите метод построения.
Литература:
- Рогановская Е. Н. Теоретико-методические основы проектирования перспективно-инновационной среды геометрического образования (II и III ступени общего среднего образования): Монография / Е. Н. Рогановская. — Могилев: МГУ имени А. А. Кулешова, 2023. — 276 с.
- Рогановский Н. М. Методика преподавания математики. Ч. 1: Общая методика / Н. М. Рогановский, Е. Н. Рогановская. — Мн.: Народная асвета, 2018. — 174 с.

