Построение сечений исключительно благоприятный материал для развития пространственного представления и воображения. Этот материал необходим для развития креативности [1, с. 336], [2, с. 119] и для более успешного изучения стереометрии, которое часто сопряжено с затруднениями именно из-за недостатка развития пространственного воображения субъектов.

Отметим, что в традиционном обучении стереометрии задачам на построение сечений в школьном курсе отводилось весьма достойное место. Об этом свидетельствует, например, Сборник задач по стереометрии в 9–10 классах Н. Рыбкина, который многие годы сопровождал учебник геометрии А. П. Киселева и заслужил не меньшую популярность.

По существу задачи на построение сечений вводятся с самых первых страниц названного Сборника и на протяжении всех его параграфов (§§ 1–25) встречаются неоднократно.

О классификации задач на построение сечений тел и методов их решения. Анализ специальной литературы (см, например, [3], [4]) позволяет упорядочить методы построения сечений следующим образом.

Методы, которые относятся к произвольным многогранникам (произвольным призмам, произвольным пирамидам — таких задач в Сборнике почти нет); методы, которые относятся к многогранникам специального вида (куб, прямоугольный параллелепипед, прямая призма и др. — таких задач подавляющее большинство).

Кроме того, можно выделить методы, которые не требуют выполнения дополнительных построений, и методы, которые требуют выполнения дополнительных построений.

Последняя группа задач и соответствующих методов наиболее многочисленная. Её в свою очередь можно также подразделить на две группы. К одной такой группе отнести методы, которые основаны только на аксиомах принадлежности стереометрии, к другой группе — методы, которые используют более широкую теоретическую базу (аксиомы стереометрии, свойства параллельности и перпендикулярности прямых и плоскостей в пространстве, свойства самих многогранников и др.).

К методам, которые опираются только на аксиомы принадлежности стереометрии и первые следствия из них, относятся метод использования линий пересечения плоскостей несмежных боковых граней (наиболее удобный для произвольных многогранников) и метод следа. По частоте употребления на первом месте стоит конкурирующий с ними метод использования свойств секущей плоскости и многогранника.

Метод внутреннего проектирования ранее не рассматривался вообще. В современных учебниках к нему стали обращаться при наличии темы о параллельном проектировании и изображении фигур в стереометрии.

Отметим также, что решение задач на построение сечений допускает также совместное применение некоторых методов (вначале один метод, на завершающей стадии — другой метод).

Все методы заключают в себе значительный развивающий потенциал и выступают содержательной основой креативного обучения . Последнее замечание можно рассматривать как предупреждение от формального подхода к задачам на построение сечений.

Еще одно замечание. На наш взгляд, в тех случаях, когда изображения фигур выполняются точно — на основании свойств изображений, правильнее говорить о чертежах, а не о рисунках. Рисунок может быть слишком произвольным, схематичным, не передавать существенные признаки условия и решения задачи.

Общая методическая схема реализации креативного обучения решению задач на построение сечений : выделение опорных задач; первоначальная характеристика метода построения сечений; ознакомление с этапами решения задачи (чтение задачи, анализ текста задачи, выполнение чертежа по условию задачи, краткая запись задачи, поиск решения задачи, поэтапное выполнение построения сечения); обобщенная характеристика метода построения сечений; решение тренировочных задач на построение сечений тел данным методом; варьирование задач: построение сечений призм и пирамид; нестандартные случаи выбора секущей плоскости; самостоятельное решение задач на построение сечений тел различной сложности. Конкретизируем эту схему применительно к ознакомлению учащихся с методом построения сечений многогранников с помощью линий пересечения плоскостей несмежных граней . На чертеже (рис. 1) изображены общие элементы задач на построение сечений — призма и пирамида, плоскость основания, плоскости двух боковых граней и прямая, по которой пересекаются две последние плоскости.

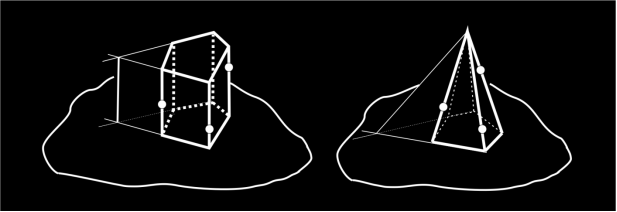
Рис. 1. Базовые элементы стереометрического чертежа

Опорная задача. Дана пятиугольная призма ABCDЕA ₁ B ₁ C ₁ D ₁ Е ₁ , X ₁ ∈ AA ₁ , X ₂ ∈ ЕЕ ₁ , X ₃ ∈ DD ₁ . Постройте сечение призмы плоскостью X ₁ X ₂ X ₃ (рис. 2).

Начнем с поиска решения задачи.

1. Некоторые стороны многоугольника сечения можно построить сразу: строим стороны X ₁ X ₂ и X ₂ X ₃

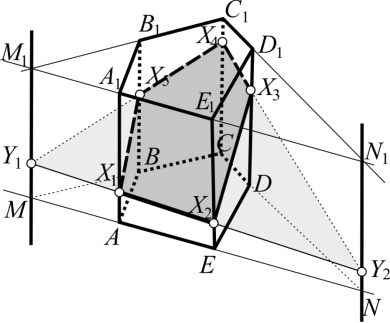
Рис. 2. Построение сечения методом пересечения плоскостей несмежных граней

2. Далее строим прямые пересечения MM ₁ и NN ₁ плоскостей несмежных боковых граней призмы, применение которых в дальнейшем составит основной замысел построения сечения. Чтобы построить эти прямые , нужно найти по две точки этих прямых (точки M,M ₁ и N,N ₁ ). Точки находятся как точки пересечения прямых, расположенных соответственно в плоскостях нижнего и верхнего оснований призмы:

М = АЕ ∩ ВС, M ₁ = A ₁ Е ₁ ∩ В ₁ C ₁ ; N = AE ∩ CD, N ₁ = A ₁ Е ₁ ∩ C ₁ D ₁ .

Далее через точки М и M ₁ проводим прямую MM ₁ , через точки N и N ₁ проводим прямую NN ₁ : МM ₁ = АA ₁ Е ₁ Е ∩ DD ₁ C ₁ C ; NN ₁ = АA ₁ Е ₁ Е ∩ СС ₁ D ₁ D.

3. Какие вершины многоугольника сечения можно построить с помощью прямых MM ₁ и NN ₁ ? Необходимо использовать аксиомы принадлежности стереометрии. Замечаем, что прямая X ₁ X ₂ пересекает обе прямые МM ₁ и NN ₁ (все три прямые лежат в одной плоскости). Строим точки пересечения: Y ₁ = X ₁ X ₂ ∩ MM ₁ , Y ₂ = X ₁ X ₂ ∩ NN ₁ . Так как точка Y ₁ принадлежит прямой MM ₁ и прямая MM ₁ принадлежит секущей плоскости, то точка Y ₁ принадлежит секущей плоскости, аналогично: так как точка Y ₂ принадлежит прямой NN ₁ и прямая NN ₁ принадлежит секущей плоскости, то точка Y ₂ принадлежит секущей плоскости.

4. Прямая Y ₂ Х ₃ принадлежит секущей плоскости. Кроме того, эта прямая лежит в плоскости боковой грани СС ₁ D ₁ D . Поэтому прямая Y ₂ Х ₃ пересекает прямую СС ₁ в некоторой точке Х ₄ , которая является четвертой вершиной многоугольника сечения: Х ₄ = Y ₂ Х ₃ ∩ СС ₁ .

5. Так как прямые Y ₁ Х ₄ и ВВ ₁ принадлежит одной плоскости — плоскости боковой грани ВВ ₁ С ₁ , то можно построить точку их пересечения — точку Х ₅ , которая является пятой вершиной многоугольника сечения: Х ₅ = Y ₂ Х ₄ ∩ BB ₁ .

Таким образом, получаем пятиугольник Х ₁ Х ₂ Х ₃ Х ₄ Х ₅ — искомое сечение, построенное с помощью линий пересечения плоскостей несмежных боковых граней.

Содержательное обобщение решения задачи. Перечислим все шаги, выполненные при построении сечения методом использования линий пересечения плоскостей несмежных боковых граней:

1. вначале строим две точки М и М ₁ , через которые проходит линия пересечения ММ ₁ первой пары непараллельных плоскостей. Каждая точка строится как точка пересечения прямых, лежащих соответственно в плоскостях нижнего и верхнего оснований;
2. строятся аналогичные две точки N и N ₁ и прямая NN ₁ для второй пары непараллельных плоскостей;
3. на этих прямых находятся точки Y ₁ и Y ₂ , которые принадлежат плоскости сечения — как точки пересечения с ними прямой Х ₁ Х ₂ , лежащей в плоскости сечения;
4. строим две новые прямые Y ₂ Х ₃ (при пересечении её с ребром СС ₁ получаем четвертую вершину многоугольника сечения Х ₄ ) и Y ₁ Х ₄ (при пересечении её с ребром ВВ ₁ получаем пятую вершину многоугольника сечения Х ₅ ). В итоге все вершины многоугольника сечения построены.

Тренировочные задачи : Рассматривается та же призма, изменяется расположение точек Х ₁ , Х ₂ и Х ₃ , эти точки могут лежать на ребрах или на их продолжениях. Варьируется выбор тела. Каждый раз построения соотносим со сделанным выше содержательным обобщением.

Нестандартные случаи задач : Рассмотрение метода на примере пятиугольной пирамиды, предполагается большая самостоятельность субъектов, действия по аналогии, перенос на новую ситуацию.

Литература:

1. Ильин Е. П. Психология творчества, креативности, одаренности / Е. П. Ильин. — СПб.: Питер, 2009. — 448 с.
2. Рогановская Е. Н. Теоретико-методические основы проектирования перспективно-инновационной среды геометрического образования (II и III ступени общего среднего образования): Монография / Е. Н. Рогановская. — Могилев: МГУ имени А. А. Кулешова, 2023. — 276 с.
3. Рогановский Н. М. Элементарная математика. Ч. IV. Стереометрия: учеб. пособие / Н. М. Рогановский, Е. Н. Рогановская. — Мн.: Адукацыя і выхаванне, 2004. — 336 с.
4. Четверухин Н. Ф. Стереометрические задачи на проекционном чертеже. Пособие для учителей. Изд. 3-е / Н. Ф. Четверухин. — М.: Учпедгиз, 1955. — 128 с.