Введение.
Большинство процессов и явления окружающего мира представляются в виде нелинейных моделей. В связи с этим появилась необходимость научиться решать именно нелинейные уравнения, не пытаясь заменить их слишком упрощенными приближенными линейными уравнениями. Одним из направлений, которое сыграло важную роль в формировании современных представлений о свойствах нелинейных волновых процессов, является теория солитонов. Набор солитонных моделей весьма узок и содержит не более двух десятков важных для практики солитонных уравнений, например, уравнение Кортевега-де-Вриза (КдВ), Нелинейное уравнение Шредингера (НУШ), Кадомцева-Петвиашвилли (КП). Sin -Gordon (SG) и т. д. [1] В связи с этим остро встал вопрос о сводимости достаточно широкого класса уравнений к солитонным уравнениям (задача редукции).
Рассмотрим способы построения двумерных интегрируемых уравнений, имеющих солитонные решения и интегрируемых с помощью обратной задачи рассеивания.
Метод построения двумерного интегрируемого уравнения, связанный с уравнением Лакса.
Пусть 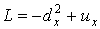 - оператор Шрёдингера,
- оператор Шрёдингера,
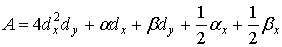 (1)
(1)
— кососимметрический оператор третьего порядка, где 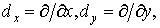
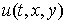 - неизвестная функция. Функции
- неизвестная функция. Функции 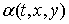 и
и 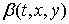 необходимо найти из уравнения Лакса
необходимо найти из уравнения Лакса 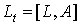 .
.
Коммутатор операторов L и A имеет вид
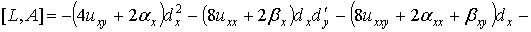
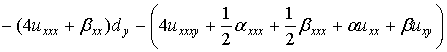 (2)
(2)
Тогда уравнение Лакса эквивалентно системе уравнений
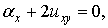
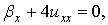
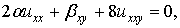
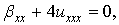
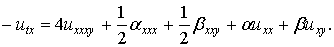 (3)
(3)
Уравнения во второй строке (3) являются следствиями уравнений первой строки, в результате находим
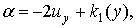
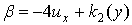 . (4)
. (4)
Будем полагать, что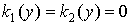 . Тогда уравнений (3) примет вид
. Тогда уравнений (3) примет вид
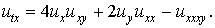 (5)
(5)
Для функций вида 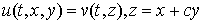 уравнение (5) переходит в уравнение Кортевага-де Вриза на функцию
уравнение (5) переходит в уравнение Кортевага-де Вриза на функцию 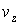
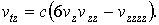 (6)
(6)
Для функций вида 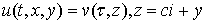 уравнение (3) переходит в уравнение
уравнение (3) переходит в уравнение
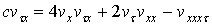 (7)
(7)
Оно также является интегрируемым модельным уравнением для распространения длинных волн в среде с нелинейной дисперсией. Если к оператору (1) добавить оператор
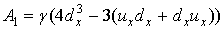 , (8)
, (8)
то из уравнения Лакса получим нелинейное уравнение вида
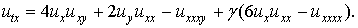 (9)
(9)
Уравнение (9) эквивалентно уравнению (5) и преобразуется в него заменой координат 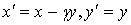 .
.
Метод построения нового двумерного интегрируемого уравнения
Пусть функция 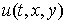 зависит от трех переменных, L — оператор Шрёдингера, оператор А — сумма операторов
зависит от трех переменных, L — оператор Шрёдингера, оператор А — сумма операторов
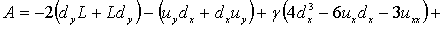
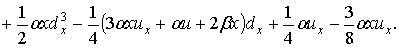 (10)
(10)
Тогда операторное уравнение
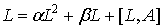 (11)
(11)
будет эквивалентно следующему уравнению
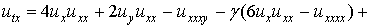
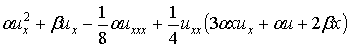 . (12)
. (12)
Это новое двумерное дифференциальное уравнение, так же как и уравнение (5), может быть решено методом обратной задачи рассеивания. [2]
Большинство известных солитонных уравнений описывают поведение функций, зависящих от двух пространственно — временных переменных. Вследствие этого актуальность приобретает задача посроения 2+1-мерного дифференциального уравнения. Рассмотрим способ получения такого уравнения из операторного уравнения Лакса
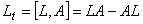 . (13)
. (13)
Теорема. Уравнение
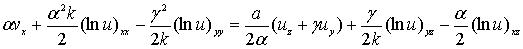 (14)
(14)
обладает парой Лакса с операторами L и А вида
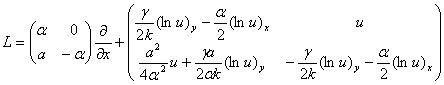 ,
,
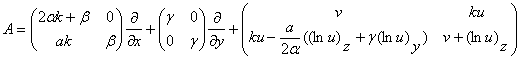 .
.
где 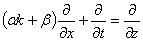 ,
, 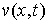 — произвольная функция.
— произвольная функция.
Доказательство. Рассмотрим частный случай, когда оператор L не содержит дифференцирования по х и имеет структуру
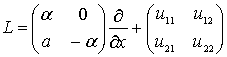 , (15)
, (15)
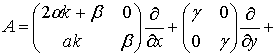
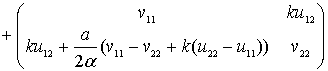 (16)
(16)
где 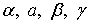 , k –произвольные постоянные, vij, uij — произвольные функции трех переменных х, у и t. Такой выбор операторов обуславливает равенство нулю коэффициентов при дифференциалах
, k –произвольные постоянные, vij, uij — произвольные функции трех переменных х, у и t. Такой выбор операторов обуславливает равенство нулю коэффициентов при дифференциалах 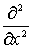 ,
, 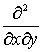 ,
, 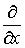 ,
, 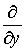 .
.
Выведем уравнение в частных производных, эквивалентное операторному уравнению Лакса. Для этого найдем элементы матричного уравнения 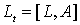 , используя обозначение
, используя обозначение 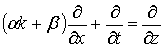 и принимая во внимание условие
и принимая во внимание условие 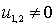 :
:
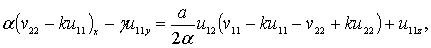 (17)
(17)
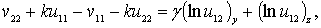 (18)
(18)
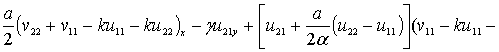
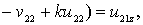 (19)
(19)
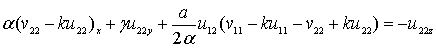 (20)
(20)
С учетом равенства (18) определим дополнительные условия так чтобы
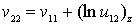 , (21)
, (21)
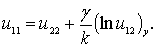 (22)
(22)
Подставим найденные значения в оставшуюся систему (10.6–9)
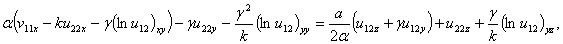 (23)
(23)
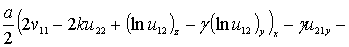
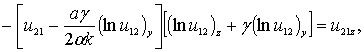 (24)
(24)
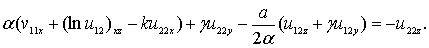 (25)
(25)
Найдем разность (23) и (25):
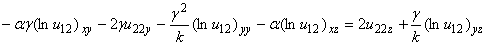 ,
,
или 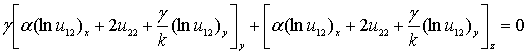 ,
,
что позволяет определить функцию 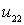
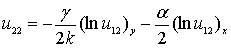 . (26)
. (26)
Выразим 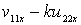 из (25)
из (25)
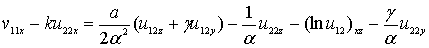 . (27)
. (27)
и выполним подстановку найденной функции (26)
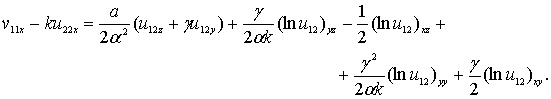
Найденное соотношение (27) подставим в (24)
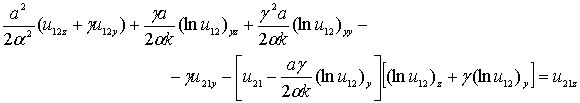
и умножим все члены на 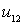
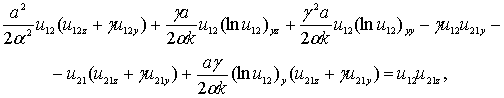
тогда выделяя полные производные, имеем
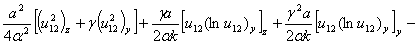
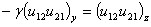
или
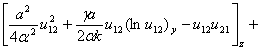 ,
,
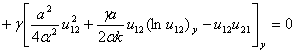
в результате можно найти функцию 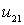
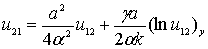 . (28)
. (28)
И так, в ходе преобразований системы (10.12–14) из (24) найдена функция 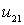 , а из (25) —
, а из (25) — 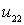 , поэтому осталось единственное уравнение (23), связывающее две функции
, поэтому осталось единственное уравнение (23), связывающее две функции 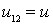 и
и 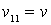
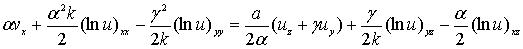 , (29)
, (29)
где 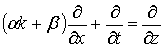 .
.
В последующих исследованиях будем считать произвольную функцию 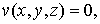 тогда уравнение примет вид
тогда уравнение примет вид
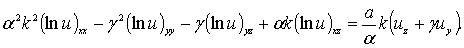 (30)
(30)
Полученное уравнение в частных производных имеет вид локального закона сохранения, при этом функция 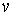 является произвольной и может описывать некоторое возмущение уравнения. При подстановке в (15), (16) найденные значения
является произвольной и может описывать некоторое возмущение уравнения. При подстановке в (15), (16) найденные значения 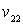 ,
, 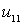 ,
, 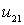 ,
, 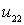 из равенств (21), (22), (28), (26) получим операторы Лакса.
из равенств (21), (22), (28), (26) получим операторы Лакса.
Уравнения 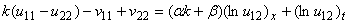 и (29) имеют общей оператор рассеяния L, а, следовательно, уравнения на собственные значения совпадают формально, но при этом собственное значение оператора L в одном случае являются постоянными, а во втором представляют собой некоторые функции, зависящие от дополнительной переменной у.
и (29) имеют общей оператор рассеяния L, а, следовательно, уравнения на собственные значения совпадают формально, но при этом собственное значение оператора L в одном случае являются постоянными, а во втором представляют собой некоторые функции, зависящие от дополнительной переменной у.
Литература:
1. Журавлев В. М. Нелинейные волны в многокомпонентных системах с дисперсией и диффузией. Точно решаемые модели. Ульяновск: УлГУ, 2001.
2. Богоявленский О. И. Опрокидывающиеся солитоны. М.: Наука. 1991.

