Введение
В работе рассматривается система уравнений вида:
![]() (1)
(1)
Частные случаи системы дифференциальных уравнений (1) рассматривались в статьях [1] — [3], в которых были получены условия, которым должна удовлетворять правая часть системы уравнений указанного вида, обладающей богатым набором законов сохранения.
В настоящей работе определены системы уравнений (1), которые обладают законами сохранения нулевого и первого порядков.
§1. Закон сохранения нулевого порядка
В этом параграфе рассматривается система уравнений (1), которая обладает законом сохранения нулевого порядка:
![]() (2)
(2)
Справедливо следующее утверждение.
Теорема 1. Система уравнений (1), которая имеет закон сохранения нулевого порядка (3), точечными преобразованиями приводится к системе вида:
![]() (3)
(3)
Доказательство.
Запишем закон сохранения нулевого порядка (2) в виде:
![]()
Перепишем последнее с учетом системы уравнений (1), а именно, заменим производные ![]() и
и ![]() .
.
![]()
Приравнивая при независимых переменных ![]() и
и ![]() получим следующую систему уравнений:
получим следующую систему уравнений:
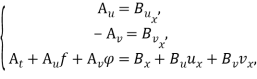 (4)
(4)
Рассмотрим случаи:
-
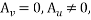
-
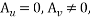
-
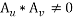 .
.
Пусть выполнен случай 1, то есть ![]() .
.
Тогда из первых двух уравнений системы (4), имеем:
![]() .
.
Далее функцию ![]() запишем в следующем виде:
запишем в следующем виде:
![]()
или ![]() , где
, где ![]() .
.
Сделаем точечную замену:
![]() (5)
(5)
Тогда система уравнений (1) согласно (2) примет вид:
![]() (6)
(6)
где ![]() .
.
Отметим, что система (6) имеет закон сохранения нулевого порядка (2), имеющий вид: ![]() .
.
Рассмотрим второй случай, когда ![]() .
.
Если ![]() , то из (4) следует, что
, то из (4) следует, что ![]() имеет вид:
имеет вид:
![]() .
.
Функцию ![]() запишем в виде:
запишем в виде: ![]()
или ![]() , где
, где ![]()
и тогда точечная замена вида:
![]() (7)
(7)
исходную систему уравнений (1) приводит к следующей системе уравнений:
![]() (8)
(8)
где ![]() .
.
При этом закон сохранения нулевого порядка (2) имеет вид:
![]() .
.
Рассмотрим последний случай, когда ![]() .
.
тогда из первых двух уравнений системы (4) следует, что:
![]() .
.
Теперь закон сохранения нулевого порядка (3) перепишем следующим образом:
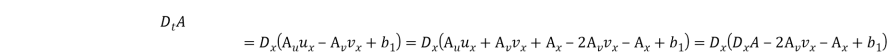
Далее сделаем точечную замену:
![]() (9)
(9)
Тогда последнее примет вид:
![]() ,
,
где ![]() .
.
Таким образом, полагая ![]() исходную систему уравнений (1) запишем в виде:
исходную систему уравнений (1) запишем в виде:
![]() (10)
(10)
Система уравнений (6) является частным случаем системы уравнений (11),если положить ![]() . Далее, если в уравнениях (8) сделать замену
. Далее, если в уравнениях (8) сделать замену ![]() , то получим систему (6).
, то получим систему (6).
Итак, система (1), имеющая закон сохранения нулевого порядка, точечными преобразованиями приводится к системе (11).Теорема доказана.
§2. Закон сохранения первого порядка
В этом параграфе рассматривается система уравнений вида (10).
В системе уравнений (11) сделаем замену:
![]() ,
,
тогда она запишется в виде:
![]() (11)
(11)
Далее перейдем от переменных ![]() ,
,![]() к переменным
к переменным ![]() .
.
Тогда закон сохранения первого порядка можно представить в следующем виде:
![]() ,(12)
,(12)
Справедлива следующая лемма.
Лемма 1. Система уравнений (11) имеет закон сохранения первого порядка (12), если справедливы следующие соотношения:
![]() , (13)
, (13)
![]() ,(14)
,(14)
![]()
![]() +
+
![]() ,(15)
,(15)
![]() , (16)
, (16)
![]() ,(17)
,(17)
![]() , (18)
, (18)
![]() . (19)
. (19)
Проведем анализ уравнений (14) — (19).
Из трех последних уравнений получаем, что ![]() имеет вид:
имеет вид:
![]()
![]() (20)
(20)
Теперь перепишем уравнения (14) — (16):
![]() , (21)
, (21)
![]()
![]() , (22)
, (22)
![]() , (23)
, (23)
Условие совместности:
![]() (24)
(24)
согласно (20),(22) и (23) примет вид:
![]() . (25)
. (25)
Рассмотрим случай, когда функция ![]() , определяющая функцию
, определяющая функцию ![]() по формуле (20), равна нулю. Имеет место следующее утверждение.
по формуле (20), равна нулю. Имеет место следующее утверждение.
Лемма 2. Пусть ![]() . Тогда система уравнений (11) имеет закон сохранения первого порядка (13), где
. Тогда система уравнений (11) имеет закон сохранения первого порядка (13), где ![]() вычисляются по формулам:
вычисляются по формулам:
![]() , (26)
, (26)
![]() , (27)
, (27)
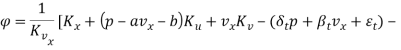
![]() . (28)
. (28)
Здесь
![]() , (29)
, (29)
![]() ,(30)
,(30)
![]() , (31)
, (31)
![]() , (32)
, (32)
![]() . (33)
. (33)
Лемма 3. Пусть ![]() . Тогда система уравнений (11) имеет закон сохранения первого порядка (13), где
. Тогда система уравнений (11) имеет закон сохранения первого порядка (13), где ![]() вычисляются по формулам:
вычисляются по формулам:
![]() , (34)
, (34)
![]() , (35)
, (35)
а φ произвольная функция.
При ![]() функции
функции ![]() и
и ![]() произвольные функции, а функции
произвольные функции, а функции ![]() определены по формулам:
определены по формулам:
![]()
![]() , (36)
, (36)
а при ![]() , эти функции определены по формулам:
, эти функции определены по формулам:
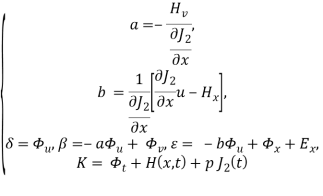 (37)
(37)
Здесь ![]() произвольная функция.
произвольная функция.
И наконец, рассмотрим случай, когда ![]() Справедливо следующее утверждение.
Справедливо следующее утверждение.
Теорема 2. Пусть ![]() , тогда система уравнений (11) имеет закон сохранения первого порядка, где функции
, тогда система уравнений (11) имеет закон сохранения первого порядка, где функции ![]() имеют вид:
имеют вид:
![]()
![]() , (38)
, (38)
![]() ,(39)
,(39)
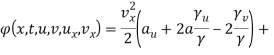
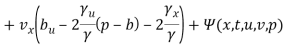 . (40)
. (40)
Здесь
![]() , (41)
, (41)
![]()
![]() , (42)
, (42)
![]() ,(43)
,(43)
![]() , (44)
, (44)
![]() ,(45)
,(45)
![]() ,(46)
,(46)
При этом выполнены следующие соотношения:
![]() (47)
(47)
![]()
![]() (48)
(48)
![]()
![]()
![]()
![]() , (49)
, (49)
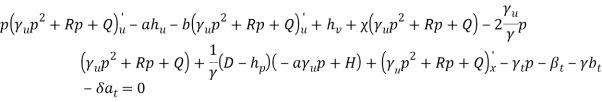 (50)
(50)
![]() ,(51)
,(51)
где r = ![]() , S =
, S = ![]() , χ =
, χ = ![]() . (52)
. (52)
Литература:
-
Михайлов А. В., Шабат А. Б. Условия интегрируемости систем двух уравнений вида
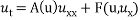 .I //ТМФ. 1985. Т. 62, № 2. С. 163–185.
.I //ТМФ. 1985. Т. 62, № 2. С. 163–185.
-
Михайлов А. В., Шабат А. Б. Условия интегрируемости систем двух уравнений вида
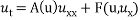 .II / / ТМФ. 1986. Т. 66, № 1. С. 47–65.
.II / / ТМФ. 1986. Т. 66, № 1. С. 47–65.
-
Шабат А. Б., Ямилов Р. И. О полном списке интегрируемых систем уравнений вида:
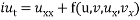 ,
, 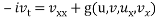 . / / Препринт. Уфа: БФАН СССР. 1985. С. 28.
. / / Препринт. Уфа: БФАН СССР. 1985. С. 28.

