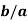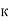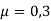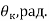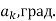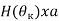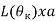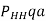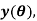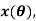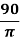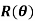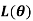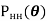В статье рассматривается алгоритм проектирования оптимального профиля в условиях минимизации энергозатрат на преодоление сопротивления при перемещении бурового и обсадного оборудования в скважинах с заданными начальной и конечной точками. В качестве модели выбрано движение материальной точки, изначально находящейся в состоянии покоя, под действием силы тяжести и трения, возникающего при движении по траектории, которая заранее неизвестна и определяется в процессе решения задачи. Решение задачи перемещения было сформулировано как принцип вариации за весьма малое время и относится ко второму нелинейному дифференциальному уравнению.

Точная аналитическая форма искомой кривой задаётся в неявном параметрическом виде и представляется в виде известных обобщённых формул брахистохроны.

Предлагается пример расчёта профиля скважины, построенного на основе предложенной модели с использованием данных месторождения.

Представляется оценка полученного экономического эффекта.

Ключевые слова: профиль, зенитный угол, траектория, обсадная колонна, ротор, циклоид.

Введение

Бурение направленных эксплуатационных скважин, в основном, выполняется по пятиинтервальному профилю, включающему начальный вертикальный участок, интервал набора зенитного угла в заданном азимуте, прямолинейный участок стабилизации зенитного угла, интервал дальнейшего набора зенитного угла и выход на конечный горизонтальный участок.

При строительстве нагнетательных скважин после интервала стабилизации в некоторых случаях зенитный угол, наоборот, снижается и реализуется вход в продуктивный пласт вертикальным стволом.

Практика буровых работ показала, что при значительных горизонтальных отклонениях забоев скважин от устья и, как следствие этого, при больших зенитных углах, поддерживать прямолинейность наклонного интервала стабилизации на достаточно протяжённых участках и одновременно сохранять неизменность азимута довольно сложно [1].

Из-за резкого увеличения сил сопротивления и в связи с этим возрастания крутящего момента на роторе при бурении интервала стабилизации дальнейшее углубление скважины сильно усложняется, а спуск обсадных колонн на проектную глубину в ряде случаев становится в принципе невозможным.

Итак, на основе анализа промыслового материала по пробуренным глубоким наклонно направленным скважинам можно сформулировать основные технологические требования к проектируемым профилям скважин. Профиль скважины должен обеспечить:

— значительное уменьшение сил сопротивления при бурении и спуске обсадных колонн на проектную глубину;

— предотвращение истирания обсадных колонн в приустьевой части скважины;

— экономию энергетических затрат и сокращение времени на бурение.

В качестве простой теоретической модели, адекватно описывающей процесс перемещения колонны бурильных или обсадных труб в скважине, выберем движение первоначально покоящейся материальной частицы вдоль неизвестной заранее траектории с заданными начальной и конечной точками (соответственно устьем и забоем). Геометрическая форма линии движения определяется в результате решения математической задачи, исходя из принципа минимизации времени прохождения траектории. В нашем случае движение материальной частицы происходит под действием собственного веса и сил сопротивления.

Методы исследования

Расчёт траектории наибыстрейшего спуска материальной частицы под действием гравитации и кулоновского трения. Найдём плоскую кривую, соединяющую две заданные точки А и В , при движении вдоль которой материальная частица, первоначально находившаяся в точке А в состоянии покоя и перемещающаяся под действием силы тяжести с учётом трения скольжения по закону Кулона — Амонтона, достигнет точки В за наименьшее время

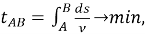
где — путь движения точки; — скорость движения.

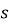
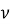
Введём декартову систему координат ХУ , где ось Х направлена по горизонтали вправо, а ось У — вертикально вниз (рис. 1). Начало координат (х = у = 0) поместим в точку А . Единичные векторы (орты) вдоль обеих осей обозначим как х и у. Тогда тангенциальный Т и нормальный N единичные векторы и каждой точке линии АВ , направленные соответственно по касательной и по нормали к траектории движения частицы, можно разложить на составляющие по координатным ортам.

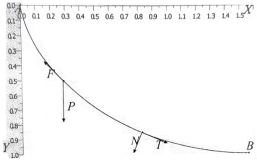
Рис. 1. Схема механических сил, действующих на движущуюся частицу

Компоненты сил, направленные вдоль траектории движения материальной частицы, определяют величину ускорения а , с которым частица перемещается из точки А в точку В в соответствии со вторым законом Ньютона

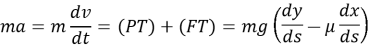
где — масса частицы; — безразмерный коэффициент трения; — ускорение свободного падения.

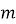
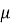
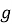
Учитывая, что , преобразуем уравнение движения следующим образом:

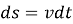
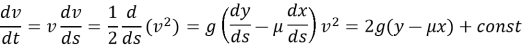
Полученное выражение представляет собой закон сохранения энергии. По условию задачи в начальной точке А (х = у = 0) частица находится в состоянии покоя, т. е. её начальная скорость равна нулю (v = 0). Таким образом, const = 0, а полное время движения вдоль линии АВ равно

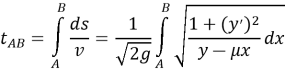
Величину этого функционала необходимо минимизировать.

В качестве варьируемой функции используем подынтегральное выражение из формулы для .

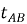
Применяя классическое уравнение вариантного исчисления Эйлера-Лагранжа [2,3], получаем для искомой траектории у(х) следующее равенство:

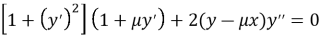
Это — обыкновенное нелинейное дифференциальное уравнение второго порядка. Оно допускает вычисление первого интеграла, который будет иметь вид

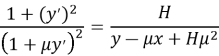
где Н — произвольная постоянная, определяемая из заданных граничных условий.

Общего решения рассматриваемой задачи в явном виде не существует. Поэтому, вводя для удобства безразмерный параметр  и выражая через него текущий угол наклона траектории АВ к горизонтали , можно записать решение поставленной задачи в параметрической форме

,

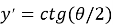
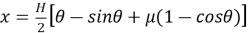
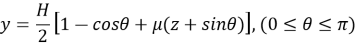
Заметим, что при найденные формулы (1) описывают хорошо известную кривую брахистохрону.

Использование результатов полученные решения

Рассмотрим оптимальную траекторию скважины. Принимаем h — длина прямолинейного вертикального участка; а — глубина скважины по вертикали, считая от точки зарезки ствола b — отклонение забоя от вертикали; L _верт. — глубина скважины по вертикали ( L _верт. =h+a ).

В начале определим значение Н из второго уравнения (1)

при

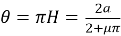
Тогда

(2)

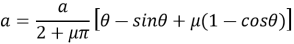
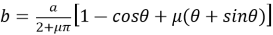
Построенная по формулам (2) траектория скважины (первая циклоида) соответствует значении и отклонения забоя , . Если забой скважины расположен левее перкой циклоиды, т. е. то траектория её будет иметь форму укороченной циклоиды, которая пересекает горизонтальную линию забоя в точке забоя.

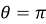
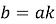
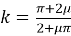
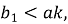
Если же забой скважины расположен правее точки т. е. , то следует рассматривать вторую циклоиду, далее третью и т. д.

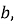
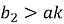
Допустим, что задано условие , т. е. . В этом случае необходимо построить вторую циклоиду, координаты которой изменяются в пределах 0–2 и 0–2 . Если находится в пределах то следует строить третью циклоиду с координатами и т. д.

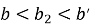
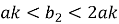
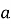
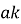
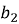
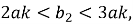
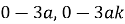
Тогда уравнения траектории, проходящей через любую точку забоя скважины, можно записать в виде

(3)

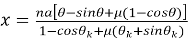
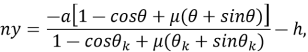
где — коэффициент, равный соответственно для первой циклоиды , для второй , третьей и т. д.

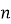
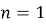
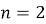
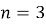
Значение наибольшего угла определяется из решения следующего трансцендентного уравнения:

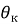
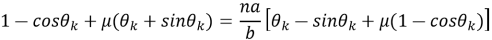
Определив , можно вычислить значение масштабного коэффициента

(4)

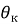
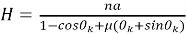
Длина скважины по стволу определяется как

(5)

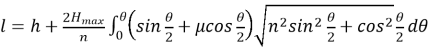
Усилие, действующее на колонну в точке зарезки ствола при её подъёме, определяется из выражения

(6)

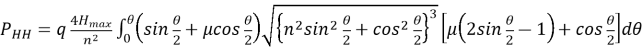
В табл. 1, 2 приводятся полученные с использованием компьютерных программ Mathcad 14 параметры траектории и величины для криволинейного интервала скважины в зависимости от отношения и .

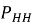
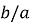
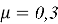
Практический пример расчёта. Рассчитать параметры криволинейного профиля скважины и бурильную колонну при бурении забойным двигателем при следующих данных: глубина скважины по вертикали — 1800, глубина зарезки — 300 м, отклонение забоя от вертикали м, перепад давления в забойном двигателе МПа, плотность раствора кг/м3. Бурильная колонна одноразмерная, составлена из труб 140х9 мм ( ).

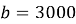
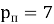
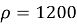
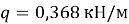
Таблица 1

Таблица 2

Из табл. 1 и 2 для соотношения и коэффициента трения определяем следующие показатели траектории скважины:

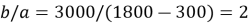
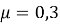
— максимальный зенитный угол на забое скважины ;

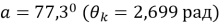
— протяжённость ствола скважины ;

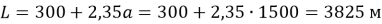
— масштабный коэффициент траектории скважины м.

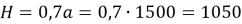
Выполним следующие предварительные расчёты:

при , м, м, , так как м, величину в формуле (3) принимаем равной 2.

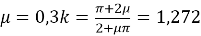
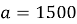
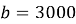
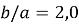
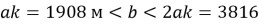
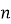
Рис. 2. Профиль скважины

Таблица 3

Тогда параметрическое уравнение профиля будет иметь вид

,

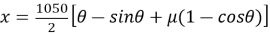
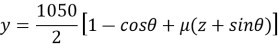
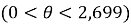
Траектория скважины приводится на рис. 2, а фрагмент расчёта параметров профиля в интервале 1659–1800 м — в табл.3.

Усилие на устье при подъёме бурильной колонны

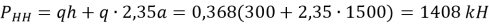
Общее усилие у устья скважины с учётом потери массы колонны в буровом растворе и перепада давления в забойном двигателе определится из выражения

кН

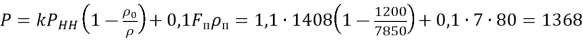
а напряжение

кН/м2

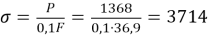
Коэффициент запаса прочности для труб группы прочности E равен

что выше допустимого 1,35.

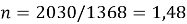
Коэффициент запаса прочности в клиновом захвате

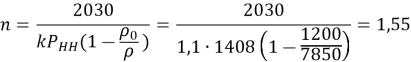
что выше допустимого .

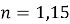
Таким образом, по пробуренным скважинам, криволинейные профили которых были рассчитаны в соответствии с изложенным алгоритмом, получены следующие результаты

— уменьшение сил сопротивления при спускоподъёмных операциях примерно на 10 снижение вращающего момента на роторе на 20 % и суммарная экономия энергетический затрат при вращении бурильной колонны в 20–25 %;

— снижение количества затяжек и постиг при бурении и спуске обсадных колонн.

— сокращение времени на бурение на 5–7 %

На разработанный профиль скважины получен патент РФ № 2370620, приоритет изобретения от 05 июня 2008 г., регистрация в Государственном реестре РФ 20.10.09.

Литература:

1. Чан Суан Дао, Ширин-заде С. А. Новые профили наклонно направленных скважин на месторождениях Белый Тигр и Дракон // Азербайджанское нефтяное хозяйство. — 1999. — № 1.- с.10–15.
2. Ректорис К. Вариационные методы и математической физике и технике. –М.: Мир, 1985.
3. Эльсгольц Л. Э. Дифференциальные уравнения и вариационное исчисление. — М.: Эдиториал УРСС, 2000.
4. Мирзаджанзаде А. Х., Крылов В. И., Аветисов А. Г. Теоретические вопросы скважин в поглощающих пластах. М., ВНИИОЭНГ, 1973, 81 с.
5. Мирзаджанзаде А. Х., Сидоров Н. А., Ширинзаде С. А. Анализ и проектирование показателей бурения. М., Недра, 1976.
6. Белонин М. Д., Славин В. И., Чилингар Д. В. Аномально высокие пластовые давления. Происхождение, прогноз, проблемы освоения залежей углеводородов: монография. СПб.: Недра, 2005. 324 с.