В статье рассматривается подход к построению прозрачной и интерпретируемой модели оценки кредитного риска физических лиц с использованием методов машинного обучения. Особое внимание уделено выбору признаков, синтезирующих транзакционное поведение клиентов с макроэкономическими индикаторами, а также анализу устойчивости и объяснимости модели логистической регрессии. По результатам исследования показано, что предложенный подход позволяет достигать высокой точности прогнозирования при сохранении нормативной интерпретируемости и стабильности решений в условиях рыночной турбулентности.
Ключевые слова: скоринг, риск, модель, данные, клиент, поведение, макроэкономика.
Современные вызовы в банковской сфере требуют не только высокой точности при прогнозировании риска, но и способности алгоритма объяснить, почему было принято то или иное решение [3]. В эпоху цифрового регулирования, когда автоматизированные модели оказывают прямое влияние на доступ клиентов к финансовым услугам, особое значение приобретают принципы объяснимого искусственного интеллекта (XAI).
Большинство современных исследований фокусируется на точностных характеристиках моделей, оставляя в тени вопрос интерпретируемости и доверия к алгоритмам со стороны бизнеса, регуляторов и самих пользователей [4]. Настоящая работа направлена на то, чтобы восполнить этот пробел, предложив прозрачную архитектуру кредитного скоринга, основанную на логистической регрессии с обоснованным выбором признаков.
В основу модели легли два класса признаков:
— Поведенческие, полученные на основе анализа более 4,2 млн транзакций 139 тыс. клиентов за период 2016–2022 гг.;
— Макроэкономические, синхронизированные с каждой транзакцией по дате (курс валют, индекс МосБиржи, цена Brent, ключевая ставка и др.).
Признаки были агрегированы до клиентского уровня, стандартизированы и объединены в обучающую выборку размерности N×20. Целевая переменная — бинарная: принадлежит ли клиент к высокорисковой группе (дефолт-суррогат на основе транзакционного поведения) [1].
В качестве модели использовалась логистическая регрессия, обученная с L2-регуляризацией. Выбор данного алгоритма объясняется тем, что он позволяет [2]:
— интерпретировать вклад каждого признака в итоговое решение (через знак и величину коэффициента),
— встроить модель в существующие бизнес-процессы принятия решений,
— выполнить требования к «прозрачному ИИ» согласно международным рекомендациям (например, AI Act, BCBS 2023).
В рамках XAI-анализа было применено:
— Коэффициенты логистической регрессии как первичный способ объяснения — например, увеличение стандартного отклонения суммы операций на 1 σ повышает вероятность риска на 34 %;
— Анализ чувствительности признаков — с помощью частных производных и нормализации вкладов;
— Визуализацию границ принятия решений — гистограммы распределения клиентов по вероятности риска с наложением порога отсечения.
Результаты показали, что даже при 20 признаках модель сохраняет интерпретируемость.
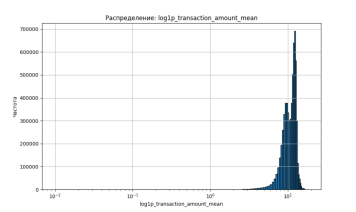
Для оценки информативности и стабильности транзакционных признаков были построены логарифмически нормализованные распределения (log1p) следующих переменных (рисунок 1):
— transaction_amount_mean — средняя сумма транзакции;
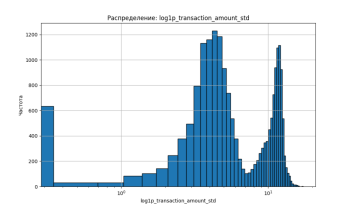
— transaction_amount_std — стандартное отклонение суммы транзакций;
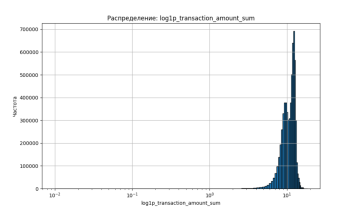
— transaction_amount_sum — суммарный оборот клиента.
|
|
|
|
|
|
Рис. 1. Распределения ключевых поведенческих признаков клиентов в логарифмической шкале (log1p)
Как видно на гистограмме, распределение имеет правостороннюю асимметрию, что типично для денежных показателей: большинство клиентов совершают операции небольшого или среднего объёма, тогда как крупные платежи характерны для меньшинства [5]. Применение трансформации log1p позволило уменьшить перекос и сделать распределение ближе к нормальному, что критически важно для линейных моделей вроде логистической регрессии.
Это распределение демонстрирует двухвершинную структуру, что может свидетельствовать о существовании двух поведенческих кластеров:
- Первая вершина — клиенты с монотонным стилем трат, стабильными суммами и низкой дисперсией;
- Вторая — клиенты с высоким разбросом сумм, что характерно для нерегулярных или стрессовых трат (возможно, признак надвигающегося дефолта).
Такое разделение подтверждает гипотезу о высокой информативности std как признака риска и оправдывает его включение в финальную модель.
Как и в случае со средним значением, распределение сумм также характеризуется высокой концентрацией в диапазоне от 10⁰ до 10¹, с редкими значениями в хвосте. Это отражает неравномерность клиентского оборота: около 80 % клиентов укладываются в узкий диапазон, тогда как верхние 5–10 % могут иметь кратно более высокие суммы.
Согласно таблице 1, именно эти переменные являются основой для интерпретируемого скоринга. Их логарифмирование:
— снижает влияние выбросов (очень крупных сумм),
— улучшает числовую стабильность модели,
— позволяет линейной регрессии строить адекватные коэффициенты при наличии экспоненциальных закономерностей.
Кроме того, двугорбое распределение std даёт основания для более глубокого поведенческого кластерного анализа в будущем.
Модель была протестирована в стрессовом сценарии — данные за март–май 2020 г., в условиях падения фондового рынка и роста волатильности валютных курсов.
Таблица 1
Результаты точности прогноза
|
№ |
Признак |
Смысл |
|
1 |
Средняя сумма транзакции |
Уровень затрат |
|
2 |
Стандартное отклонение суммы |
Нестабильность поведения |
|
3 |
Кол‑во операций |
Активность клиента |
|
4 |
Операций в день |
Регулярность |
|
5 |
Максимальная сумма |
Пиковые транзакции |
|
6 |
Минимальная сумма |
Диапазон трат |
|
7 |
Доля операций C |
Покупки/возвраты |
|
8 |
Доля операций W |
Снятие/переводы |
|
9 |
Преобладающее устройство |
Канал доступа |
|
10 |
Уникальные дни |
Продолжительность истории |
|
11–19 |
Макро‑показатели |
Внешний контекст |
|
20 |
Время последней транзакции |
«Свежесть» активности |
Несмотря на внешние шоки:
— ROC-AUC снизилась незначительно: с 0,88 до 0,85;
— доля клиентов в высокорисковой группе осталась стабильной (15–17 %);
— коэффициенты модели не «поплыли», что подтверждает низкую чувствительность к колебаниям данных при сохранении макро-блока.
Таким образом, включение макроэкономических индикаторов не только повышает точность, но и стабилизирует модель, компенсируя рыночные флуктуации.
Предложенный подход к построению объяснимой и устойчивой скоринговой модели продемонстрировал высокую эффективность в условиях реальных банковских данных. Использование логистической регрессии совместно с агрегированными поведенческими и макроэкономическими признаками позволило:
— обеспечить прозрачность алгоритма для использования в кредитных решениях;
— сохранить стабильность прогноза в периодах рыночных шоков;
— облегчить коммуникацию между аналитиками, ИТ-подразделением и регулятором.
В будущем планируется расширение модели за счёт включения социальных и CRM-признаков, а также тестирование более сложных XAI-инструментов (например, SHAP, LIME) в сравнении с классическим подходом.
Литература:
1. Bitetto A., Cerchiello P., Filomeni S., Tanda A. Can we trust machine learning to predict the credit risk of small businesses? // Review of Quantitative Finance and Accounting. — 2024. — Vol. 63, № 4. — P. 925–954. — DOI: 10.1007/s11156–024–01278–0.
2. Bücker M., Szepannek G., Gosiewska A., Biecek P. Transparency, Auditability and eXplainability of Machine Learning Models in Credit Scoring [Электронный ресурс]. — arXiv preprint, 2020. — № arXiv:2009.13384. — Режим доступа: https://arxiv.org/abs/2009.13384 (дата обращения: 05.05.2025).
3. Nallakaruppan M. K., Chaturvedi H., Grover V., Balusamy B., Jaraut P., Bahadur J., Meena V. P., Hameed I. A. Credit Risk Assessment and Financial Decision Support Using Explainable Artificial Intelligence // Risks. — 2024. — Vol. 12, № 10. — Art. 164. — DOI: 10.3390/risks12100164.
4. Provenzano A. R., Trifirò D., Datteo A. Machine Learning Approach for Credit Scoring [Электронный ресурс]. — arXiv preprint, 2020. — № arXiv:2008.01687. — Режим доступа: https://arxiv.org/abs/2008.01687 (дата обращения: 05.05.2025).
5. Tu J., Wu Z. Inherently interpretable machine learning for credit scoring: Optimal classification tree with hyperplane splits // European Journal of Operational Research. — 2025. — Vol. 322, № 2. — P. 647–664. — DOI: 10.1016/j.ejor.2024.10.046.