В статье решена задача имитационного модулирования средствами AnyLogic.
Ключевые слова: имитационная модель, моделирование, IT, компьютерное модулирование.
Постановка задачи:
Двухпроцессорный вычислительный комплекс (ВК) обслуживает три автоматизированных рабочих места (АРМ). Первое АРМ имеет абсолютный приоритет по отношению к остальным, а второе — более высокий приоритет по отношению к третьему АРМ. От первого АРМ поступают запросы на обслуживание, интервалы между которыми распределены равномерно [t1,t2] с. Интервалы времени поступления запросов от второго и третьего АРМ распределены по экспоненциальному закону с параметрами t3 и t4 соответственно. На обслуживание одного запроса 1-й категории любой процессор затрачивает время, экспоненциально распределенное с параметром t5 с, 2-й категории — t6 с, 3-й категории — t7 c. В оперативной памяти ВК организован накопитель емкостью L запросов.
Каждый процессор имеет конечную надежность. Длительность интервалов между отказами распределена по экспоненциальному закону с параметром t8 с. Длительность восстановления распределена по нормальному закону с параметрами t9 c и t10 c. При отказе любого процессора обслуживаемые и прерванные запросы теряются.
Исходные данные:
L — ёмкость накопителя = 5 запросов
t1 — средний интервал времени поступления запросов от АРМ1 = 32
t2 — среднеквадратическое отклонение интервала времени поступления запросов от АРМ1 = 5
t3 — средний интервал времени поступления запросов от АРМ2 = 25
t4 — средний интервал времени поступления запросов от АРМЗ = 42
t5 — среднее время обработки запросов от АРМ1 = 11
t6 — среднее время обработки запросов от АРМ2 = 7
t7 — среднее время обработки запросов от АРМЗ = 9
t8 — средний интервал времени возникновения отказов = 8000
t9 — среднее время восстановления = 18
t10 — среднеквадратическое отклонение времени восстановления = 2
Koef — коэффициент изменения t9 и t10 = 1
Созданию системы, действующей в реальном мире, предшествует моделирование — создание и анализ системы–заместителя, которая повторяет основные характеристики исходной, но позволяет снизить расходы (времени или денег) требуемые для проведения экспериментов [1].
По Ляпунову, математическое моделирование — это опосредованное практическое или теоретическое исследование объекта, при котором непосредственно изучается не сам интересующий нас объект, а некоторая вспомогательная искусственная или естественная система (модель), находящаяся в некотором объективном соответствии с познаваемым объектом, способная замещать его в определённых отношениях и дающая при её исследовании, в конечном счёте, информацию о самом моделируемом объекте [3].
Среди математических моделей, позволяющих адекватно описать и проводить анализ широкого класса систем, следует выделить имитационные модели.
В данной статье используется среда моделирования AnyLogic. AnyLogic — программное обеспечение для имитационного моделирования, разработанное российской компанией The AnyLogic. Инструмент обладает современным графическим интерфейсом и позволяет использовать язык Java для разработки моделей [2].
Построение модели
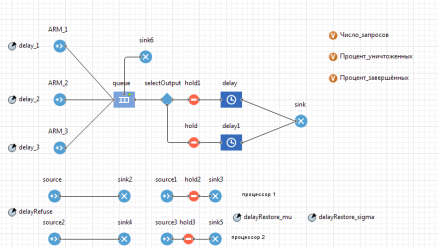
Рис. 1. Исследуемая модель
Проведём следующие исследования модели:
1. В течение 2 ч функционирования двухпроцессорного вычислительного комплекса исследуем зависимость вероятности потерь запросов от:
— емкости накопителя,
— интервалов времени выхода из строя,
— времени восстановления процессоров.
Для исследования нам понадобятся следующие переменные.
Рис. 2. Переменные
Таблица 1
Анализ работы системы в зависимости от ёмкости памяти
|
Ёмкость накопителя |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
Вероятность потери запроса |
23,3 |
18,4 |
8,4 |
8,3 |
6 |
6,1 |
3 |
2,8 |
1,1 |
1 |
Таблица 2
Анализ работы системы в зависимости от времени работы процессора
|
Время работы процессора до отказа |
600 |
650 |
700 |
750 |
800 |
850 |
900 |
950 |
1000 |
1050 |
|
Вероятность потери запроса |
8,3 |
6,9 |
6,8 |
6,5 |
5,7 |
4,3 |
4,1 |
4 |
4 |
3,9 |
Таблица 3
Анализ работы системы в зависимости от времени восстановления процессора
|
Мат ожидание (время восстановления) |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
21 |
|
Вероятность потери запроса |
5,3 |
5,4 |
5,6 |
5,3 |
6,2 |
5,9 |
6,3 |
6 |
6,3 |
6,2 |
Анализ результатов
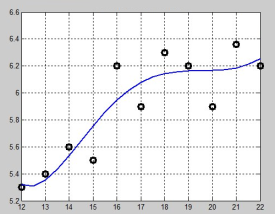
Рис. 3. Визуализация анализа работы системы в зависимости от времени восстановления процессора
В ходе выполнения этой работы были получены основные навыки решения задач по автоматизации технологических процессов в среде имитационного моделирования AnyLogic, что включает в себя проведение научно — исследовательской и проектно-конструкторской работы в области исследования и разработки сложных систем; способность ставить и проводить имитационные эксперименты с моделями процессов функционирования систем на современных ЭВМ для оценки вероятностно — временных характеристик систем. В результате выполнения работы получены результаты о работе сервера с учетом различной интенсивности генерации запросов.
Литература:
- Николенко С. Д. Глубокое обучение. Погружение в мир нейронных сетей: — Питер СПб.: ВАС, 2018. — 480 с.
- Бэзнис Б. В. Java для начинающих. Объектно-ориентированный подход в построение интерфейса Web-приложений. — СПб.: ВАС, 2018. — 680 с.
- Рашид Т. Г. Создаём нейронную сеть. — Вильямс, 2017. — 272 с

