Настоящая статья является продолжением работы [1], в которой приведены основные свойства квадратичного числового образа. Там утверждается, что квадратичный числовой образ определен, если дано разложение и , где и гильбертово пространство, а пространство линейных ограниченных операторов в гильбертовом пространстве . Тогда оператор всегда записывается в виде блочно–операторной матрицы

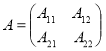(1)

с линейными ограниченными операторами , . Для неограниченного линейного оператора в , его область определения необязательно должна быть разлагаемой как прямая сумма подпространств , и следовательно, утверждение о том, что оператор имеет представление (1) является дополнительным предположением. В этом случае

.

Для удобства сначала дадим определение числового образа оператора . Пусть и — скалярное произведение и норма в , , соответственно.

Для линейного оператора в гильбертовом пространстве с областью определения его числовой образ определяется следующим образом:

.

Пусть — одномерное комплексное пространство, - гильбертово пространство квадратично интегрируемых (комплекснозначных) функций, определенных на , . Рассмотрим случай ,

, , , ;

, , , .

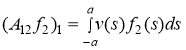Здесь –вещественные постоянные, а – вещественнозначная непрерывная функция на . В этих предположениях оператор , определенный по формуле (1) и действующий в гильбертовом пространстве , является ограниченным и самосопряженным.

Рассмотрим уравнение для собственных значений

, .

Это уравнение эквивалентно следующей системе уравнений

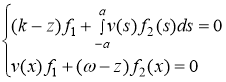. (2)

Случай 1: пусть . Тогда система уравнений (2) записывается в виде

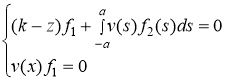. (3)

Видно, что если и , то система уравнений (3) превращается в тождество. Так как , имеем, что . Тем самим

.

Это и означает, что число является бесконечнократным собственным значением оператора .

Случай 2: пусть теперь . Тогда из второго уравнения системы уравнений (2) для имеем

. (4)

Подставляя полученное выражение (4) для в первое уравнение системы уравнений (2) имеем, что число является собственным значением оператора тогда и только тогда, когда

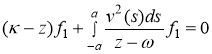
или

.

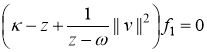Если , то в силу (4) имеем , т. е. , который противоречит тому, что число является собственным значением оператора . Поэтому . Следовательно,

.

Найдем нули этого уравнения. Простые вычисления показывают, что нули равны

.

Таким образом, и являются простые собственные значения оператора и . Мы получили следующие заключение:

1. Для существенного спектра оператора имеет место равенство:

.

2. Для дискретного спектра оператора имеет место равенство:

.

Причем обе собственные значение являются простыми.

3. Для числового образа оператора имеет место равенство:

.

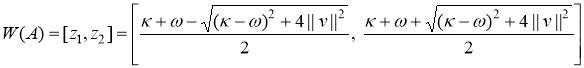Литература:

1. И. Б. Куланов. Основные свойства квадратичного числового образа. Молодой учёный, — 2016, –№ 13 (117), — С. 41–44.