В статье исследуется моделирование поведения частиц, обладающее электрическим дипольным моментом во внешнем электрическом поле. Рассмотрены устойчивые дипольные образования и их взаимодействие с ионными парами.

Ключевые слова: диполь, ионизация, электрическая частица, физико-математическая модель, вычислительный эксперимент, методы Рунге-Кутты.

Введение

Работа посвящена численному моделированию поведения молекул, обладающих электрическим дипольным моментом и взаимодействующих с ионными парами во внешнем электрическом поле. С этой целью предложена математическая модель движения большого числа таких частиц во внешнем поле. Для решения этих уравнений применяется явный метод Рунге-Кутты-Мерсона пятого порядка с контролем точности и устойчивости.

1. Электрическая дипольная частица

В качестве типичной электрической дипольной частицы рассмотрим молекулу воды . Известно [3], что масса атома кислорода масса атома водорода расстояние между атомами и а угол (рис. 1).

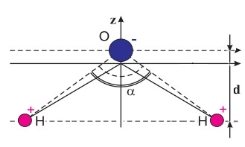
Рис. 1. Геометрическая схема молекулы воды

Поскольку основная масса атомов сосредоточена в их ядрах с размерами порядка (что значительно меньше межъядерного расстояния ), мы будем моделировать атомы водорода и кислорода материальными точками.

Уголковая конфигурация (рис. 1) и смещение электронных оболочек атомов водорода к атому кислорода приводят к возникновению в молекуле воды электрического дипольного момента (рис. 2)величиной , направленного от центра иона кислорода к середине прямой, соединяющей центры ионов водорода [3, 5].

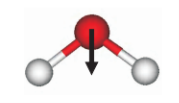
Рис. 2. Схематическая замена молекулы воды на ее дипольный момент

2. Математическая модель

Известно [1, 7], что в атмосфере в значительном количестве присутствуют ионные пары. Например, при ультрафиолетовой ионизации молекулы воды получается два иона:

(2)

Рассмотрим в качестве заряженных частиц пару и со следующими параметрами [1]:

– масса положительно заряженного иона:

– масса отрицательно заряженного иона:

– численное значение заряда иона : (3)

– численное значение заряда иона :

В качестве электрической дипольной частицы используем молекулу воды, описанную в разделе 1.

Для описания движения частицы введем инерциальную [2] декартову систему координат . Движение дипольной частицы представим в виде суперпозиции поступательного и вращательного движений. Для дипольной частицы определим поступательное движение перемещением центра масс, а вращательное – вокруг этого центра. Для описания поступательного движения дипольной частицы выпишем силу, действующую на ее центр масс, и используем второй закон Ньютона. Вращательное движение смоделируем под действием вращательного момента, определяемого относительно центра масс. 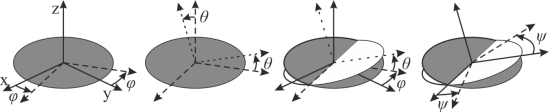Для описания вращательного движения введем также локальную подвижную систему координат , жестко закрепленную с частицей. Тогда вращение молекулы отождествляется вращением этой подвижной системы координат, описываемым с помощью углов Эйлера [2], интерпретация которых изображена на рис. 3. Углы называются углами прецессии, нутации и собственного вращения соответственно.

Постановка задачи. Рассмотрим дипольных частиц с массой , диагональным тензором инерции и вектором дипольного момента заданными в подвижной системе координат, привязанной к главным центральным осям тензора инерции, . Для каждой j-той дипольной частицы на каждый момент времени в инерциальной декартовой системе координат определим следующие величины:

– радиус-вектор центра масс дипольной частицы;

– вектор поступательной скорости центра масс;

– вектор угловой скорости относительно центра масс;

– модуль вектора дипольного момента;

– углы Эйлера.

Здесь и далее символ «» означает, что величина задана в подвижной системе координат.

Рассмотрим также заряженных частиц с массой и зарядом , .

Для -той заряженной частицы в каждый момент времени в инерциальной декартовой системе координат определим следующие величины:

– радиус-вектор центра масс заряженной частицы;

– вектор поступательной скорости центра масс.

Требуется для -той дипольной частицы, , определить на момент времени следующие величины: , , ,, а для каждой -той заряженной частицы – значения ,.

Уравнения движения. Взаимодействие дипольных частиц осуществляется посредством поля, порожденного всеми диполями и внешним полем. Известно, что напряженность [5] полного поля, действующего на -тую дипольную частицу, описывается формулой

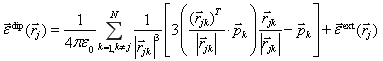,(4)

где – электрическая постоянная, , – внешнее электрическое поле, действующее на -тую дипольную частицу. Функция потенциальной энергии взаимодействия -той молекулы воды с полным дипольным полем определяется формулой

.(5)

Известно, что сила , действующая на центр масс -той дипольной частицы, представима в виде

(6)

В качестве дифференциального уравнения, описывающего поступательное движение -той дипольной частицы, используем второй закон Ньютона:

, ; .(7)

Уравнение (7) сведем к системе обыкновенных дифференциальных уравнений первого порядка посредством использования компонент вектора скорости:

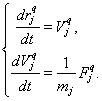
; .(8)

После проведения несложных преобразований с учетом (4)–(8) для частиц с дипольных моментом получим следующую систему уравнений:

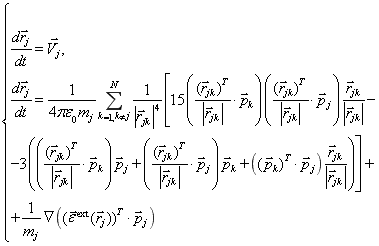
.(9)

В свою очередь, взаимодействие заряженных частиц осуществляется посредством поля, порожденного диполями; поля, порожденного взаимодействием ионов между собой и внешним полем. Напряженность поля, созданного дипольными частицами и действующего на -тую заряженную частицу нетрудно получить, зная, что полное поле, созданное дипольными частицами, описывается формулой (4). Таким образом,

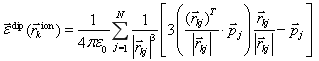,(10)

где – электрическая постоянная, .

Поле, порожденное взаимодействием ионов, описывается [4] формулой

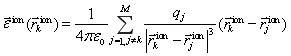. (11)

Согласно принципу суперпозиции и с учетом (10), (11), получаем, что полное поле, действующее на -тую заряженную частицу:

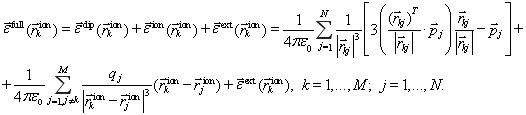(12)

Для нахождения силы, действующей на центр масс заряженной частицы, воспользуемся законом Кулона [4]:

.(13)

Пользуясь теми же рассуждениями, что и для (9), с помощью (7)–(8) получим систему обыкновенных дифференциальных уравнений (ОДУ) первого порядка, состоящую из скалярных уравнений:

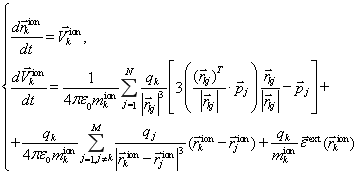
(14)

Вращательное движение -той дипольной частицы опишем вращением частицы вокруг ее центра масс под действием момента сил , который определим векторным произведением

, .(15)

Для описания вращательного движения каждой -той дипольной частицы сопоставим ей локальную подвижную систему координат , жестко закрепленную с дипольной частицей. Таким образом, вращение каждой -той дипольной частицы отождествим с вращением -той подвижной системы координат. Описание вращения подвижной системы координат осуществим с помощью углов Эйлера [2]. Исходя из определения углов Эйлера, матрица перехода [6] от подвижной системы координат к инерциальной системе имеет вид:

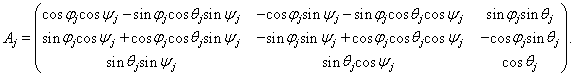
Аналогично построена матрица перехода от инерциальной системы координат к подвижной

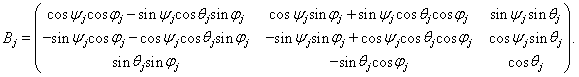
Вращательное движение каждой -той дипольной частицы опишем дифференциальным уравнением моментов, которое в подвижной системе координат имеет вид:

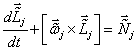, .(16)

Здесь – момент импульса -той дипольной частицы, который определим в виде:

, .(17)

Поскольку каждая -тая дипольная частица жестко закреплена с соответствующей подвижной системой координат , то элементы тензора инерции не меняются со временем:

; .(18)

Учитывая (18), в скалярном виде имеем

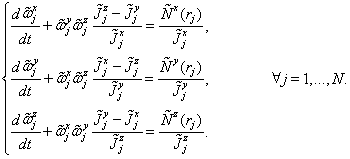(19)

Уравнения (19) называют динамическими уравнениями Эйлера, характеризующими скорость изменения угловой скорости , заданной в локальной подвижной системе координат . Определим изменение во времени самой подвижной системы координат. Для этого выпишем уравнения, характеризующие связь между производной по времени от углов Эйлера и угловой скоростью [6]:

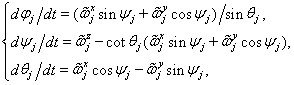
.(20)

Интегрирование системы (19)–(20), содержащей в себе скалярных уравнений, в общем случае может быть выполнено только численно.

Начальные данные. Пусть вычислительная область – сфера диаметра. В качестве диполей рассмотрим молекулы воды. Для дипольных частиц с приемлемой для нас степенью точности известны [1] их физические параметры:

; ; ;

; .(21)

На начальный момент времени поступательную и угловую скорости каждой частицы определим равными нулю

, .(22)

Углы Эйлера и координаты радиус-вектора будем задавать случайным образом с учетом следующих ограничений:

, , , .(23)

Минимально допустимое расстояние между центрами масс дипольных частиц определим, как три минимальных длины частицы вдоль линии её дипольного момента:

.(24)

Для ионов в качестве начальных данных будем использовать их физические характеристики (3). Также на начальный момент времени поступательные скорости каждой заряженной частицы определим равными нулю

.(25)

Компьютерная арифметика использует ограниченную запись вещественных чисел. Для традиционных языков программирования максимальная точность представления вещественного числа составляет 15 значащих цифр. Поэтому для корректных вычислений желательно, чтобы отношение максимального числа к минимальному по модулю числу не превышало 10¹⁵. Исходя из этого диаметр вычислительной области зададим как .

Проведем масштабирование единиц измерения с параметрами, указанными в [10]:

, , , (26)

Тогда, с учетом (26) вместо (21)–(23), получим следующие значения параметров для частиц с дипольным моментом:

(27)

и ограничения

(28)

Для заряженных частиц из (3) с учетом (26) получим:

масса положительно заряженного иона:

масса отрицательно заряженного иона:

численное значение заряда иона : (29)

численное значение заряда иона:

3. Численное решение

Для поиска численного решения системы ОДУ, состоящей из уравнений (9), (14), (19)–(20), использовались различные методы из семейства явных численных методов типа Рунге-Кутты [8] с контролем точности и устойчивости.

Вычислительный эксперимент. Изначально была проведена апробация и сравнение численных методов решения систем ОДУ на тестовых задачах. Наиболее точные расчеты за меньшее время вычислений получены с помощью метода Мерсона [9] пятого порядка точности. Кроме этого был проведен ряд расчетов для тестирования всей программы. Вычислительный эксперимент состоит в следующем. Расположим дипольные частицы в плоскости цилиндра диаметром равном , ось цилиндра параллельна оси . Начальные данные будем задавать с учетом (27)–(29). Направление дипольных моментов и положение заряженных частиц зададим случайным образом в пределах вычислительной области. Внешнее электрическое поле , направленное противоположно оси , будем считать равным внешнему электрическому полю Земли [7]:

.

Под действием внешнего электрического поля дипольные частицы упорядочиваются вдоль линий напряженности внешнего поля, а заряженные частицы «облепляют» образованную таким образом дипольную «косичку» (рис. 4).

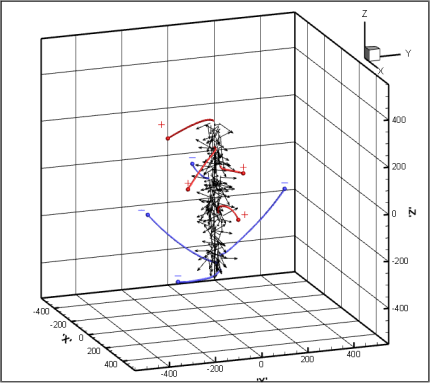
Рис. 4. Траектории движения заряженных частиц.

“+”– положительно заряженные, “–” – отрицательно

Таким образом, устойчивое во времени образование из частиц с электрическим дипольных моментом создает собственное электрическое поле, на порядки превышающее взаимодействие ионов между собой. Ближе к верхнему отрицательному полюсу такого образования скапливается положительный заряд, а ближе к нижнему положительному – отрицательный, усиливая тем самым созданное диполями поле.

Этот эффект может объяснить образование в атмосфере так называемого тёмного лидера, предшествующего обратной вспышке молнии.

Заключение

В рамках статьи была предложена и описана математическая модель, описывающая взаимодействие электрических дипольных частиц с заряженными частицами. Проведена верификация созданного программного комплекса для устойчивых во времени образований из электрических диполей и их взаимодействия с ионными парами. Проведен вычислительный эксперимент, демонстрирующий усиление электрического поля исходного дипольного образования за счет взаимодействия с ионными парами.

Работа поддержана Проектом 14-01-00147 Российского научного фонда.

Литература:

1. Куриленко О.Д. Краткий справочник по химии // 4-е изд., исправл. и доп. – Киев: Наукова думка, 1974. – 992 с.
2. Ландау Л.Д. Теоретическая физика в 10 т. Т. 1: Механика. Электродинамика / Л.Д. Ландау Е.М. Лифшиц. – 3-е изд., перераб. и доп. – М.: Наука, 1973. – 208 с.
3. Aлешкевич В.А. Механика сплошных сред. Лекции / В.А. Алешкевич, Л.Г. Деденко, В.А. Караваев. – М: Изд-во физ. фак. МГУ, 1998. – 92 с.
4. Арцимович Л.А. Движение заряженных частиц в электрических и магнитных полях. Учебное пособие / Л.А. Арцимович, С.Ю. Лукьянов. – М: Изд-во «Наука», 1978. – 225 с.
5. Киттель Ч. Введение в физику твердого тела. – М.: Наука, 1978. – 791 с.
6. Поляхов Н.Н. Теоретическая механика / Н.Н. Поляхов, С.А. Зегжда, М.П. Юшков; под ред. проф. Н.Н. Поляхова. – Л.: изд-во Ленингр. ун-та, 1985. – 536 с.
7. Тарасов Л.В. Ветры и грозы в атмосфере Земли: Учебное пособие / Л.В. Тарасов. – Долгопрудный: Издательский Дом «Интеллект», 2011. – 280 с.
8. Бахвалов Н.С. Численные методы. – М.: Наука, 1975.
9. Захаров А.Ю. Некоторые результаты сравнений эффективности методов решения систем обыкновенных дифференциальных уравнений: Препринт № 125 / А.Ю. Захаров. – М.: Изд. ИПМ АН СССР, 1979. – 25 с.
10. Лабутин А.А. Краткие сведения о международной системе единиц измерений (СИ). – Киев: Вища школа, 1975. – 88 с.